3.3.7 Построение кривых д-разбиения в плоскости двух настроечных коэффициентов арв-сд

Для построения границы устойчивости в плоскости двух параметров регулятора необходимо структурно представить описание системы в виде обобщенной ПФ , составленной относительно лишь двух, выделенных для исследования и оптимизации, каналов (коэффициентов усиления по ним) регулирования. Остальные каналы должны иметь известное математическое описание (ПФ звеньев и фиксированные значения настроечных параметров), которое учтено в . В этом случае представляет собой ПФ системы, разомкнутой только по выделенным каналам. Например, при построении кривых Д-разбиения в плоскости коэффициентов по каналам отклонения частоты ( ) и производной этого отклонения ( ), искомая структурная схема имеет вид, представленный на рис. 3.11.

Рис. 3.11. Одноконтурная структурная схема многоконтурной системы регулирования

По полученным ПФ разомкнутой системы и выделенного канала регулирования строится ХП, который является знаменателем соответствующей ПФ замкнутой системы:

, (3.116)

где – обобщенная ПФ системы, разомкнутой только по выделенным каналам; , – ПФ звеньев каналов регулирования по отклонению и производной отклонения частоты напряжения шин в соответствии с соотношениями (3.87, 3.88).

При переходе к частотным изображениям заменой из знаменателя (3.116) может быть получен характеристический годограф (годограф Михайлова), содержащий в явном виде исследуемые настроечные коэффициенты по каналам регулирования:

. (3.117)

Для того чтобы определить значения и , которые на текущей (расчетной) частоте сдвигают годограф Михайлова в начало координат, т.е. выводят систему на границу устойчивости , необходимо для каждого заданного значения частоты решить относительно искомых двух коэффициентов два уравнения, обеспечивающие равенство нулю действительной и мнимой части выражения для характеристического годографа:

. (3.118)

Семейство решений данной системы в виде образует совокупность точек границы устойчивости или кривой Д-разбиения в плоскости двух выбранных параметров. Пример такой кривой приведен на рис. 3.12. Напомним, что все точки плоскости (комбинации пар коэффициентов), расположенные левее границы, при перемещении по ней в направлении увеличения расчетной частоты, определяют область устойчивости. И наоборот, любая комбинация коэффициентов, выбранная правее границы, приводит к потере устойчивости системы, т.е. к приобретению правой пары корней.

Можно заметить, что замена в выражении (3.116) приведет к построению годографа и кривых Д-разбиения, отражающих не границу устойчивости, а некоторые кривые, смещенные относительно границы вовнутрь области устойчивости на заданную величину . Последнее соответствует поиску условий (комбинаций коэффициентов регулятора) для расположения корней на оси комплексной плоскости, смещенной влево от начала координат на величину (рис. 3.12).

Для пояснения методики проведем следующие структурные преобразования. Вначале представим принципиальную схему АРВ-СД (рис. 3.9) структурно таким образом, чтобы в ней в явном виде присутствовали коэффициенты усиления и ПФ по всем каналам регулирования (рис. 3.13) в соответствии с полным законом регулирования (соотношение (3.90)).

Рис. 3.12. Вывод пары комплексных корней с мнимой частью при помощи найденной комбинации коэффициентов на границу устойчивости (ось «j») и на ось равной степени устойчивости («_з+j»)

Рис. 3.13. Полная структурная схема АРВ-СД

Затем структурную схему замкнутой по всем каналам системы (рис. 3.10) более подробно раскроем с учетом схемы АРВ-СД (рис. 3.13) и соотношений (3.90), (3.96), (3.97). Заметим, что на рис. 3.11, 3.13 для сокращения в обозначениях ПФ опущен оператор « ».

Пунктирной линией на рис. 3.14 выделена структура упомянутой выше обобщенной ПФ (3.116). Нетрудно видеть, что при её использовании структурная схема, представленная на рис. 3.14, трансформируется в одноконтурную (рис. 3.11). Искомая ПФ может быть рассчитана по известным функциям элементов и звеньев, входящих в .

Рис. 3.14. Структурная схема системы, замкнутой по всем каналам регулирования

В практических задачах оптимизации настроечных параметров регуляторов часто используется экспериментальная АФЧХ реальной системы, разомкнутой лишь по исследуемому каналу, с рабочими коэффициентами усиления по всем каналам регулирования. При наличии такой ЧХ отпадает необходимость в трудоемких расчетах соответствующей обобщенной ПФ и последующем переходе к ее частотному изображению. В этом случае процедура построения границы устойчивости начинается непосредственно с использования соотношения (3.117).

Следует заметить, что методика применения экспериментальных ЧХ в виде готовых выборок комплексных чисел для построения областей (границ) устойчивости является эффективной для реальных систем. Однако она не позволяет оценивать качество ПП (степень устойчивости ) при настройках, выбранных внутри области, поскольку для построения кривых равного качества необходимо полное математическое описание звеньев в виде ПФ или других операторных соотношений, позволяющих перейти к частотным изображениям при .

В целях лучшего понимания изложенного выше теоретического материала выполним построение кривой Д-разбиения для ВИЗ 00. Для этого приравняем ХП ПФ (3.109) к нулю:

. (3.119)

Из формулы (3.119) получим систему уравнений относительно двух переменных – настроечных коэффициентов усиления :

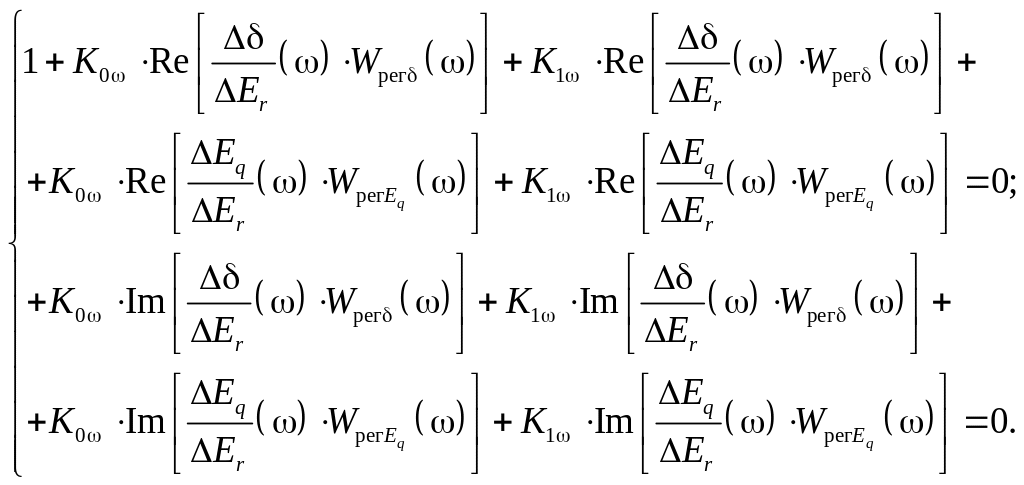.(3.120)

Решив систему (3.120) для каждого значения частоты относительно коэффициентов усиления каналов стабилизации частоты напряжения шин статора, определим комбинации , обеспечивающие равенство нулю действительной и мнимой части выражения для характеристического годографа (3.120). Графическая интерпретация решения (3.120) представлена на рис. 3.15, где , .

Рис. 3.15. Кривая Д-разбиения

Область устойчивости здесь определим как зону, ограниченную кривой Д-разбиения, осью абсцисс и ординат . Выберем из этой области различные комбинации настроечных параметров , для которых рассчитаем СЧ системы с помощью программы “KORNI.exe”. Результаты сведём в табл. 3.4.

Как видно из табл. 3.4, любая комбинация настроечных коэффициентов усиления , взятая внутри области устойчивости, обеспечивает общую статическую устойчивость ЭС с различными запасами. Так, если при значении коэффициентов дел., дел. достигается степень устойчивости системы с^–1, то при комбинации дел., дел. она уже равна с^-1, что соответствует границе устойчивости. Как подобрать такую комбинацию уставок регулятора сильного действия, при которых обеспечивается наибольшая степень устойчивости , а следовательно, и наилучшее качество ПП. Решение этого вопроса будет исследовано в подразделе 3.3.9.

Таблица 3.4

СЧ системы при различных комбинациях

№ комб.	Комбинация настроечных параметров		СЧ системы
	К0ω, дел.	К1ω, дел.
1	0,0	0,0	-0,067 ±j 5,37 -0,248 ±j 0,0
2	0,5	1,0	-0,072 ±j 5,26 -0,238 ±j 0,0
3	1,0	1,5	-0,087 ±j 5,14 -0,222 ±j 0,0
4	2,0	5,0	-0,085 ±j 4,38 -0,211 ±j 0,0
5	3,0	6,0	-0,118 ±j 4,18 -0,169 ±j 0,0
6	3,5	8,5	-0,111 ±j 3,72 -0,165 ±j 0,0
7	4,0	9,5	-0,124 ±j 3,54 -0,143 ±j 0,0
8	5,0	5,0	-0,061 ±j 0,0 -0,223 ±j 4,38
9	5,0	2,0	-0,053 ±j 0,0 -0,263 ±j 5,02
10	6,0	10,0	-0,015 ±j 0,0 -0,219 ±j 3,45
11	6,2	20,0	-0,0036 ±j 0,0 -0,169 ±j 1,72