3.3.4. Частотные характеристики и передаточные функции параметров режима без учёта действия арв-сд

Частотные характеристики – это амплитудно-фазовые соотношения приращений параметров режима при задании гармонического возмущения на обмотку возбуждения генератора. Эти характеристики целесообразно использовать при анализе границ колебательной устойчивости и взаимного влияния каналов регулирования по различным параметрам режима и их производным. Рассмотрим ЧХ электропередачи, включающей СГ, который работает через внешнюю реактивность на шины неизменного напряжения (рис. 3.2). При изучении этих характеристик можно использовать соотношения, получаемые из решения линеаризованных уравнений Горева-Парка [5], которые применяют для исследования ПП. Не учитывая для простоты выкладок демпферные контуры и исключая составляющие, обусловленные быстрозатухающими ПП и изменением скорости вращения ротора относительно синхронной оси, запишем уравнения в виде

; (3.36)

; (3.37)

; (3.38)

. (3.39)

В уравнениях (3.38), (3.39) и далее литера «р» используется как символ дифференцирования переменной во времени (не путать с литерой «Р», обозначающей активную мощность генератора).

Линеаризованные уравнения ПП электропередачи, работающей на мощную приемную систему, запишем в виде

, (3.40)

где

; (3.41)

; (3.42)

. (3.43)

Уравнение движения в полных единицах

. (3.44)

В относительных единицах :

. (3.45)

Используя статорное уравнение , имеем

. (3.46)

Необходимо привести уравнение (3.42) к базисным переменным. Тогда

. (3.47)

Поскольку линеаризовать необходимо по , то

; (3.48)

. (3.49)

Уравнение движения ротора (3.44), (3.45) примет следующий вид:

. (3.50)

В формуле (3.50) исключим с помощью выражения

. (3.51)

Тогда

. (3.52)

Таким образом, имеем

. (3.53)

В уравнении (3.53) , то есть . Поэтому линеаризованное уравнение принимает вид

. (3.54)

Исключим из (3.43) , используя (3.36), и получим

; (3.55)

; (3.56)

. (3.57)

Тогда уравнение (3.43) примет вид

. (3.58)

Обозначим зависимость

; (3.59)

. (3.60)

Таким образом, система двух линеаризованных уравнений с двумя неизвестными примет вид

(3.61)

или

(3.62)

Обозначим выражения в системе (3.62):

; (3.63)

; (3.64)

; (3.65)

. (3.66)

Тогда исходную систему уравнений (3.62) можно записать в виде

(3.67)

Решив уравнение (3.67) относительно и , найдем ПФ параметров регулирования разомкнутой системы и :

; (3.68)

. (3.69)

Знаменатель выражений (3.68) и (3.69) является ХП, имеющим корни, характеризующие общие динамические свойства, в том числе и статическую устойчивость системы. Данный полином 3-го порядка, имеет одну комплексную пару корней (колебательная составляющая движения) и действительный корень (апериодическая составляющая):

. (3.70)

Положим, что к обмотке возбуждения генератора приложено гармоническое возмущение с амплитудой и частотой . Тогда изменение переменных и также будет гармоническим. Заменив в выражениях (3.68) и (3.69) оператор дифференцирования на , найдем ЧХ системы и  :

; (3.71)

. (3.72)

В полной форме эти выражения имеют вид

; (3.73)

. (3.74)

Частные производные в выражении приращения электромагнитной мощности из (3.52) определяются следующим образом:

; (3.75)

. (3.76)

Для лучшего понимания изложенного материала ниже приведён пример исследования статической устойчивости и построения ЧХ разомкнутой системы для ВИЗ 00.

Величину синхронизирующей мощности определим согласно выражению (3.75): . Поскольку , то можно утверждать, что система в разомкнутом состоянии является устойчивой.

Определим корни ХП, численное выражение для которого получим согласно (3.70):

. (3.77)

Для нахождения корней полинома (3.77) воспользуемся программой “KORNI.exe”:

.

Результаты решения кубичного уравнения представим в форме табл. 3.3.

Таблица 3.3

Собственные значения характеристической матрицы

Затухание, с–1	Частота, Гц
–0,067	5,37
–0,240

Отметим полученные корни на комплексной плоскости (рис. 3.6).

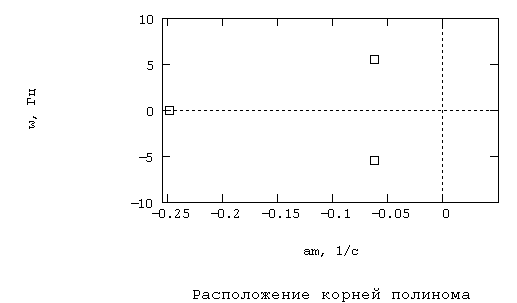
Рис. 3.6. Расположение корней ХП на комплексной плоскости

Поскольку все три корня ХП находятся в левой полуплоскости относительно мнимой оси (рис. 3.6), т.е. имеют отрицательные вещественные части, то исследуемую систему в разомкнутом состоянии можно считать устойчивой. В то же время комплексно-сопряжённый корень находится в опасной близости к границе устойчивости. Следовательно, необходимо предусмотреть мероприятия по повышению запасов устойчивости системы.

Для построения ЧХ разомкнутой системы по каналу регулирования угла напряжения статора запишем соотношение для нахождения АФЧХ согласно (3.73):

.

Значение частоты будем изменять в пределах от 0 до 10 Гц с шагом . Вид построенных ЧХ разомкнутой системы по каналу регулирования представлен на рис. 3.7, 3.8.

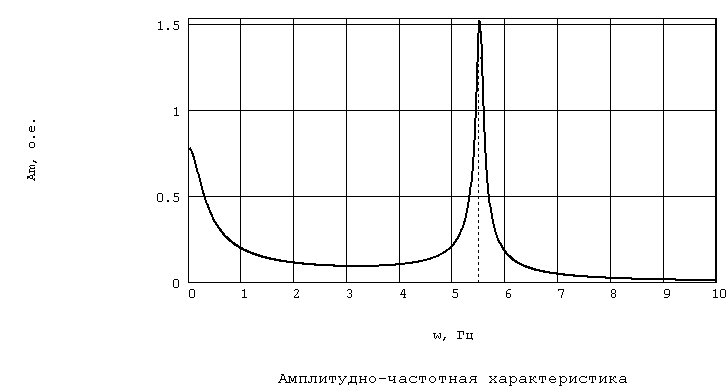
Рис. 3.7. АЧХ разомкнутой системы по каналу регулирования угла

Р ис. 3.8. ФЧХ разомкнутой системы по каналу регулирования угла