3.3.3. Построение угловой характеристики активной мощности электропередачи, оценка запаса статической устойчивости

Запас статической устойчивости является одним из основных показателей, определяющих допустимость режима работы ЭС. Обеспечение запаca необходимо главным образом для того, чтобы сохранить устойчивость ЭС при нeрeгулярных колебаниях мощности и удаленных коротких замыканиях, когда основная противоаварийная автоматика и специальные средства повышения устойчивости не действуют. Поэтому практическое значение имеют лишь те режимы работы ЭС, которые достаточным образом удалены от границы апериодической устойчивости. Величина, характеризующая расстояние от указанной границы до точки исследуемого режима, и будет являться запасом статической устойчивости.

В общем случае запас устойчивости может характеризоваться самыми различными показателями [12]:

1) величиной синхронизирующей мощности генераторов системы;

2) расстоянием кривой годографа Михайлова от начала координат;

3) кривой Д-разбиения;

4) значением вещественной части самого правого корня ХУ;

5) величиной якобиана уравнения УР или свободного члена ХУ системы.

Однако эти показатели не обладают достаточной информативностью, так как не имеют четкой интерпретации и наглядности, зависят не только от режима, но и от выбранных математических моделей и не характеризуют слабые звенья ЭС. Поэтому наиболее правильным является непосредственное сопоставление точки исследуемого режима с границей области апериодической устойчивости.

Для простейших схем ЭС определение запаса устойчивости не связано с какими-либо затруднениями, так как утяжеление исходного режима осуществляется изменением одного регулируемого параметра. Например, в схеме показанной на рис. 3.2, утяжеляемым параметром является активная мощность генератора (рис. 3.5) при данном значении передаваемой мощности (например, отвечающей точке «а» на рис. 3.5).

Рис. 3.5. Угловая характеристика простейшей ЭС

Максимальное значение электромагнитной мощности генератора равно отношению амплитуды синусоидальной характеристики мощности к индуктивному сопротивлению системы:

, (3.29)

где – максимальное значение электромагнитной мощности генератора; – синхронная ЭДС генератора; – напряжение на шинах генератора; – индуктивное сопротивление системы.

характеризует запас устойчивости данного режима, количественное значение которого определяется согласно следующему выражению [8]:

, (3.30)

где .

Режим ЭС считается допустимым, если полученный коэффициент запаса устойчивости удовлетворяет неравенству [7]

, (3.31)

где – нормативный коэффициент, равный 20 % для нормального режима, 8 % – для после аварийного.

Для нахождения активной мощности воспользуемся формулой

. (3.32)

При этом значение фиктивной ЭДС может быть вычислено по двум равнозначным формулам:

1) . (3.33)

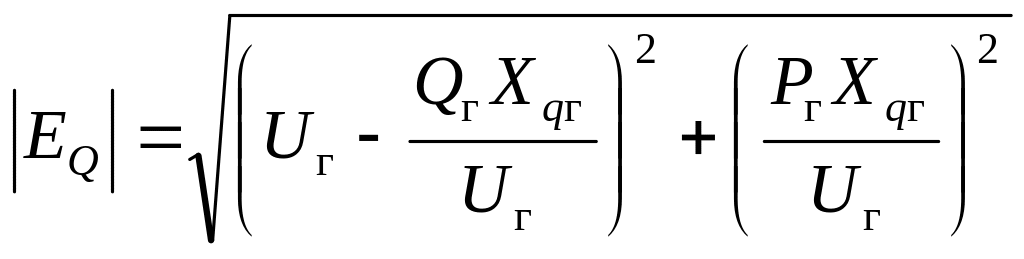2) . (3.34)

Путём изменения в формуле (3.32) значений угла от 0 до 180 построим угловую характеристику электропередачи, вид которой представлен на рис. П.2.2.

Коэффициент запаса апериодической устойчивости определяется согласно выражению

, (3.35)

где – предел по передаваемой мощности, соответствующий значению активной мощности при ; – механическая мощность, приложенная к ротору со стороны первичного двигателя, направленная на вращение ротора и соответствующая значению активной мощности при .