2.5. Уравнения установившегося режима синхронной машины

Формально уравнения УР СМ могут быть получены из системы (2.22) вычеркиванием всех членов, содержащих производные величины во времени:

1) . (2.30)

2) . (2.31)

7) . (2.32)

Нумерация слева в формулах (2.30)–(2.32) соответствует принятой для исходной системы уравнений движения (2.22). На рис. 2.7 показаны проекции вектора напряжения, совмещенного с синхронно вращающейся действительной осью (+1) на оси q и d.

Рис. 2.7. Векторная диаграмма напряжений в установившемся режиме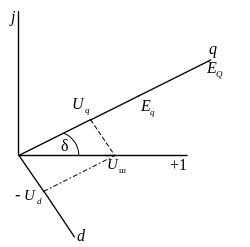

В соответствии с рис. 2.7 для проекций векторов справедливы следующие соотношения:

; (2.33)

.(2.34)

Запишем и проанализируем вначале уравнения УР в статорных цепях СМ, вытекающие из первого и второго уравнений движения (все переменные, описывающие УР, будем обозначать прописными буквами):

1) . (2.35)

2) . (2.36)

Прежде чем преобразовать уравнения (2.35), (2.36), введем понятие фиктивной ЭДС E_Q, связанной с E_q таким соотношением:

. (2.37)

Заметим, что для неявнополюсных машин (например, турбогенераторов, у которых статорные обмотки симметричны: ) . Это обстоятельство позволяет утверждать, что вектор ЭДС E_Q должен совпадать по направлению с поперечной осью q (рис. 2.7).

Исключим из уравнения (2.35) E_q, заменив ее соотношением (2.37). Затем, домножим уравнение (2.36) на (-j) и сложим с (2.35). В результате преобразования получим

, (2.38)

или короче:

. (2.39)

Выражения (2.38) и (2.39) проиллюстрированы векторной диаграммой УР СМ на рис. 2.8.

Рис. 2.8. Векторная диаграмма СГ

Таким образом, используя ЭДС E_Q, можно представить СМ в УР её работы в виде ЭДС, включенной за сопротивлением Z_q (при пренебрежении r – за x_q). Очевидно, что выражение, записанное при использовании комплексной плоскости, вещественная ось которой совмещена с осью q, а мнимая – с осью d, будет справедливо при любом другом положении осей комплексной плоскости. В частности, удобно совместить вектор напряжения U с вещественной осью новой комплексной плоскости (рис. 2.8).

Величина полного тока в этом случае в соответствии с рис. 2.8 может быть определена как

.

Тогда

. (2.40)

Очевидно, что модуль этой ЭДС равен E_Q и может быть найден по формуле

. (2.41)

Аргумент ЭДС E_Q определяется как

. (2.42)

После нахождения величины и положения на комплексной плоскости ЭДС E_Q, а следовательно, и направления поперечной оси ротора СМ могут быть найдены q- и d-составляющие всех переменных. Для нахождения q- и d-составляющих векторов тока могут быть использованы следующие формулы:

, . (2.43)

Таким образом, при известных параметрах СМ , , имея в качестве исходных данных параметры , , по соотношению (2.43) могут быть рассчитаны искомые токи УР в статорной цепи I_q и I_d, а следовательно, и остальные параметры: , , и т.д.

При исследовании УР возможна обратная ситуация, когда по известным , , , , необходимо вычислить активную (Р) и реактивную (Q) мощности генератора. Воспользуемся соотношением (2.40) и выразим из него P и Q через остальные переменные, для простоты пренебрегая активным сопротивлением r, полагая :

. (2.44)

Напомним, что вектор U совмещен с вещественной осью, E_a и Е_р – соответственно проекции вектора на действительную и мнимую оси. Домножим обе части (2.44) на U и, кроме этого, числитель и знаменатель правой части на (-j):

, (2.45)

то есть

, . (2.46)

К таким же соотношениям для активной и реактивной мощности можно прийти, анализируя векторную диаграмму СМ на рис. 2.8.

В частности, из диаграммы следует:

.

При домножении обеих частей равенства на получим выражение для действительной мощности:

. (2.47)

Покажем, что последнее из уравнений УР (2.32) можно преобразовать в используемое ранее соотношение (2.26):

=

. (2.48)

Соотношения (2.46)–(2.48) широко используются при описании и исследовании УР СМ. На рис. 2.9 представлена соответствующая синусоидальная зависимость активной мощности от электрического угла, называемая угловой характеристикой [7]:

. (2.49)

Рис. 2.9. Угловая характеристика мощности и соответствующая ей векторная диаграмма