2.3 Необходимость линеаризации систем

Отметим еще раз, что все выводы по использованию традиционных моделей и методов синтеза желаемых динамических свойств (п. 1.3) справедливы только для линейных систем, в уравнения движения которых входят переменные только в первой степени.

Из соотношений (2.22) следует, что некоторые уравнения движения ЭС нелинейны, поскольку включают произведения и тригонометрические зависимости переменных, характеризующих состояние системы. Например, взаимные произведения переменных состояния ( и ).

Для применимости хорошо разработанного аппарата анализа и синтеза линейных систем исходные ДУ необходимо линеаризовать в некоторой области исследуемого режима. Для этого нужно рассчитать совокупность нормальных предполагаемых режимов работы системы. Например, один из них характеризуется параметрами , , , ,…, , . Тогда седьмое уравнение (2.22) в результате линеаризации будет выглядеть так:

. (2.24)

Заметим, что данное уравнение записано уже относительно отклонений переменных в области рассчитанного режима.

Ниже будет показано, что нелинейная составляющая в седьмом уравнении системы (2.22), при традиционных аналитических исследованиях, трансформируется в нелинейную зависимость ЭДС (E_Q) и напряжения шин (U_ш), включающую тригонометрическую функцию от электрического угла (δ). При этом седьмое уравнение (2.22) приобретает вид

, (2.25)

где нелинейная составляющая (*) является выражением для активной мощности генератора:

. (2.26)

Соотношение (2.26) называется угловой характеристикой активной мощности генератора и играет важную роль при анализе устойчивости системы [7, 8]. Для упрощения анализа ПП в ЭЭС необходимо прибегать к методу линеаризации вблизи рабочей точки режима. Суть его состоит в том, что нелинейные зависимости параметров друг от друга аппроксимируются касательной прямой в некоторой точке «а» (рис. 2.6).

Рис. 2.6. Пример линеаризации в рабочей точке угловой характеристике мощности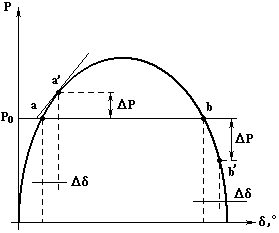

Точка «а» определяет УР системы. Если предположить, что возмущения приводят к незначительным отклонениям режима от рабочей точки, то нелинейная зависимость в области этих отклонений между активной мощностью, ЭДС и электрическим углом (2.26), может быть заменена на линейную:

, (2.27)

где K₁, K₂ – коэффициенты пропорциональности, зависящие от режима (от расположения рабочей точки на угловой характеристике). В частности, изменяющимися параметрами в (2.26), (2.27) являются E_Q и . Значения U_ш и x_г заданы и неизменны. Пусть рабочий режим генератора выбран и характеризуется значениями переменных и . Тогда линеаризация нелинейной зависимости осуществляется с использованием частных производных, вычисленных в точке рабочего режима:

. (2.28)

Окончательно седьмое линеаризованное уравнение примет вид

, (2.29)

где K₁ и K₂ определяются из (2.28).

Таким образом, применение линеаризации для анализа статической устойчивости требует обязательного определения (предварительного расчета) рабочего УР. Все выводы по статической устойчивости системы будут справедливы только для данного режимного состояния системы.