2.3 Модель отказов и восстановления воздушной линии электропередачи

Потеря работоспособности воздушных линий происходит в результате внезапных отказов. Воздушная линия электропередачи является системой состоящей из нескольких элементов – опоры, провода и изолятора. Каждый элемент характеризуется своей надежностью. Граф состояний воздушной линии представлен на рис. 2.

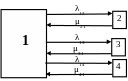
Рисунок 2 – Граф состояний воздушной линии электропередачи

В 1 состоянии воздушная линия работоспособна. В состоянии 2 отказывает провод, в состоянии 3 – изолятор, в состоянии 4 – опора. Отказы происходят с интенсивностью λ₁₂, λ₁₃ и λ₁₄. Устранение отказов происходит с интенсивностями μ₂₁, μ₃₁ и μ₄₁.

Коэффициент готовности воздушной линии электропередачи представляется выражением

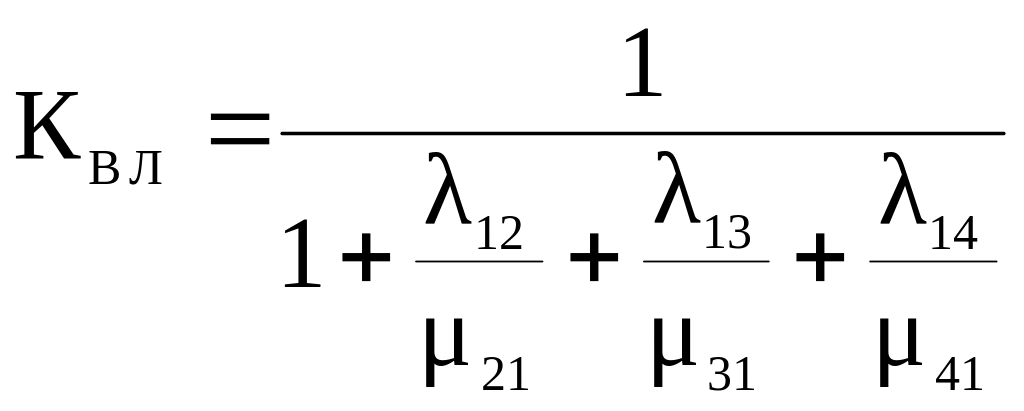. (18)

Аналитическое выражение (18) для коэффициента готовности воздушной линии электропередач представляет собой вероятность безотказной работы линии после выхода на стационарный режим работы.

Таблица 4 – Статистический ряд средней наработки на отказ Т и среднего времени восстановления τ элементов воздушной линии ВЛ1 длиной 100 км, соответственно, провода, изолятора и опоры

Тпр	Тиз	Топ	τпр	τиз	τоп
0,455 г	0,323 г	0,435 г	16 ч	10 ч	21 ч

Приведем данные таблицы 4 к единым единицам измерения, для этого выразим

τ_пр = 1,826 ∙ 10^-3 г, τ_из = 1,141 ∙ 10^-3 г, τ_оп = 2,397 ∙ 10^-3 г.

Интенсивности отказов и восстановления находятся по выражениям

, , , , , .

Определим значения λ₁₂, λ₁₃, λ₁₄, μ₂₁, μ₃₁, μ₄₁ для ВЛ1 длиной 15 км

, , ,

, , .

Определим коэффициент готовности для ВЛ1 длиной 15 км

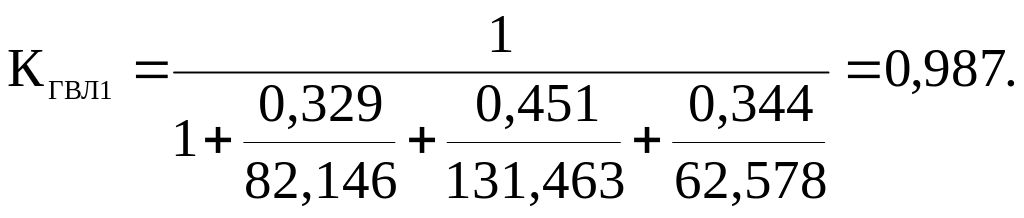
Таблица 5 – Статистический ряд средней наработки на отказ и среднего времени восстановления элементов воздушной линии ВЛ2 длиной 100 км, соответственно, провода, изолятора и опоры

Тпр	Тиз	Топ	τпр	τиз	τоп
0,370 г	0,252 г	0,212 г	20 ч	25 ч	35 ч

Приведем данные таблицы 5 к единым единицам измерения

τ_пр = 2,283 ∙ 10^-3 г, τ_из = 2,853 ∙ 10^-3 г, τ_оп = 3,995 ∙ 10^-3 г.

Определим значения λ₁₂, λ₁₃, λ₁₄, μ₂₁, μ₃₁, μ₄₁ для ВЛ2 длиной 50 км

, , ,

, , .

Определим коэффициент готовности для ВЛ2 длиной 50 км

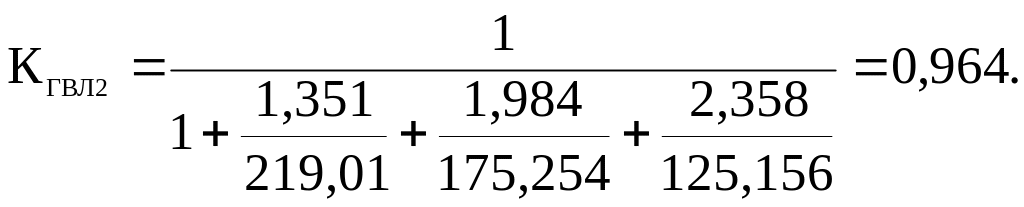
Рассматриваемая система электроснабжения находится на стационарном режиме работы, поэтому коэффициент готовности ВЛ является вероятностью безотказной работы.

2.4 Модель отказов и восстановления

ПОДСТАНЦИОННОГО ОБОРУДОВАНИЯ (ПОДСТАНЦИИ)

Основным элементом подстанции является силовой трансформатор. Подстанцию рассмотрим как объект условно состоящий из двух последовательно соединенных элементов. В одном из которых может появиться внезапный отказ, а в другом постепенный. Вероятность безотказной работы представим как произведение двух независимых событий соединенных последовательно относительно надежности

Р_по(t) = Р_в(t) ∙ Р_п(t).

Дальнейший расчет проведем как и для трансформатора. Статистические данные наработки на отказ для внезапных и постепенных отказов подстанции приведены в табл. 6.

Таблица 6 – Статистический ряд внезапных и постепенных отказов подстанции

X, ч	X, ч	X, ч	У, ч	У, ч	У, ч
17411	20304	17913	30912	32604	34386
18083	4121300	18767	31675	33417	35159
18938	20817	19454	32450	34194	31362
20133	17741	21158	33225	34968	32137
20646	18596	19621	34002	31208	32912
17572	19279	21329	34775	31982	33801
18425	20475	19792	31054	32758	34578
19108	20988	21567	31829	33609	36325
Т		λ	Уср		λ
190400		5,2523Е-7 1/ч	33100		3,0211Е-5 1/ч

В теории надежности в качестве основного закона времени безотказной работы при внезапных отказах подстанции принимается показательное распределение

Р_в(t) = е^-λt.

Постепенные отказы подстанции происходят в основном по причине износа изоляции. Износ хорошо согласуется с трехпараметрическим законом Вейбулла

.

Окончательно имеем

.

Параметр показательного закона λ находим из уравнения

,

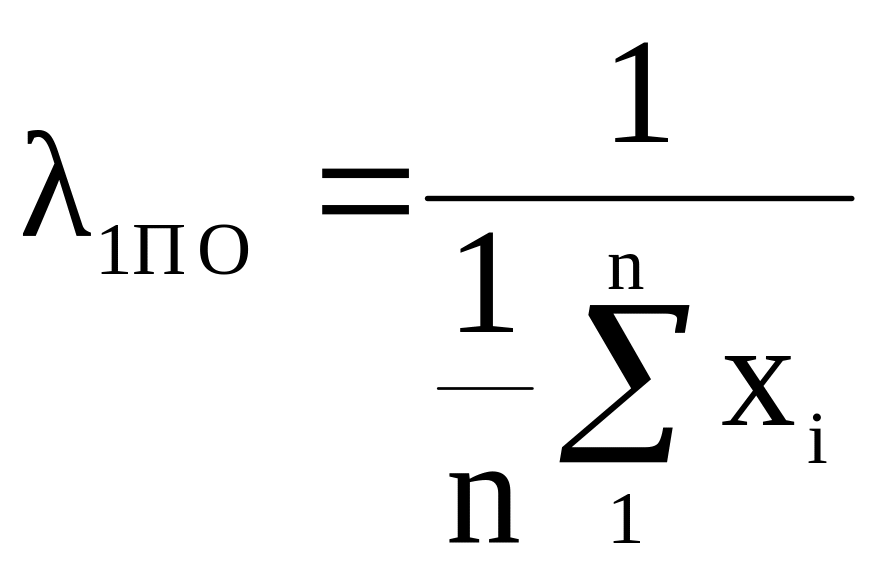где х_i – значение наработки i-го внезапного отказа.

Среднее время безотказной работы при внезапных отказах

.

Оценим параметры распределения трехпараметрического закона Вейбулла. Для этого вычислим значения У_ср, S_в. Среднее значение наработки при постепенных отказах

Среднее квадратическое отклонение σ равно

Значение S_в составляет

_,

где .

По таблице приложения 1 через известное значение S_в находим величину параметра в. По этой же таблице находим значение С_в, используя которое определим величину параметра с

с = У_ср - а∙К_в.

Средняя наработка постепенных отказов

Т_2по = У_ср.

Средняя интенсивность постепенных отказов

.

Результирующая интенсивность отказов оборудования подстанции составляет

Среднее время безотказной работы оборудования подстанции

Интенсивность восстановления подстанционного оборудования определим по формуле (18) используя данные статистического ряда, представленном в табл. 7.

Таблица 7 – Статистический ряд времени восстановления внезапных и постепенных отказов подстанционного оборудования

восстановление
16,6	20,0	22,8	19,8
25,6	25,9	19,6	21,4
18,0	24,6	19,4	21,2
18,4	22,0	17,1	18,6
21,3	21,1	17,5	17,5
Т = 20,4196 ч		μ = 0,04897 1/ч

Среднее время восстановления и интенсивность восстановления подстанционного оборудования определим по формулам

Среднее время восстановления подстанционного оборудования

Коэффициент готовности подстанции

.

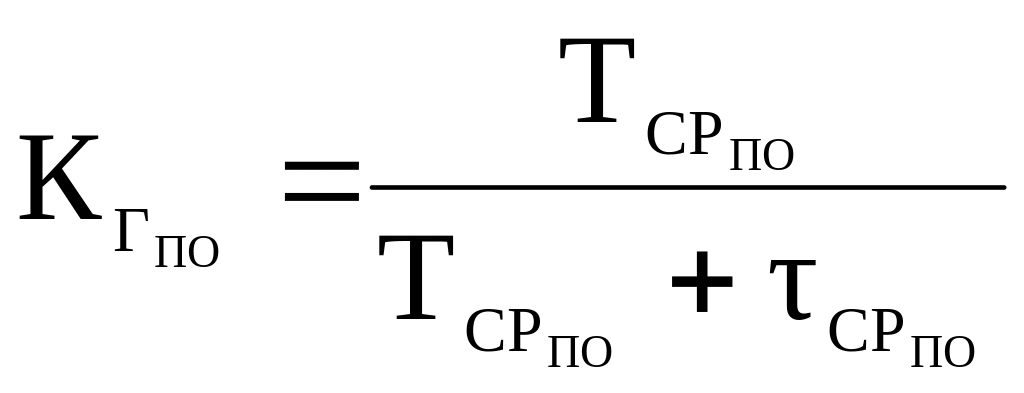
Подстанции А, Б, В одного типоразмера и работает в одинаковых условиях эксплуатации, поэтому они все имеют одинаковый коэффициент готовности.

На стационарном режиме работы коэффициент готовности подстанционного оборудования является вероятностью безотказной работы.