Аналитические модели смо

Аналитические модели применяют только для частных случаев относительно простых СМО. Для сложных систем необходим ряд допущений, что снижает адекватность модели:

1) используется дисциплина FIFO;

2) время обслуживания заявок выбирается в соответствии с экспоненциальным законом распределения;

3) входные потоки должны быть стационарными, ординарными (невозможность одновременного поступления двух заявок на вход) и с отсутствием последействия.

Марковскими цепями называют процессы с конечным множеством состояний и с отсутствием последействия. Они подходят для описания большинства СМО. Характеризуются множеством состояний S, матрицей вероятности переходов из одного состояния в другое и начальным состоянием. Представляют в виде графа, в котором вершины соответствуют состояниям цепи, дуги – переходам, веса дуг – вероятностям перехода, если время дискретно или интенсивностям, если время непрерывно.

Имитационное моделирование смо

Имитационные модели, созданные в традиционных языках программирования получаются громоздкими, поэтому используют специальные языки программирования на системном уровне. Различают языки ориентированные на описание событий, средств обслуживания или маршрутов движения заявок (процессов). Выбор языка определяет структуру модели и методику ее построения.

Языки ориентированные на средства обслуживания используются при функционально-логическом и более детальных уровнях описания объектов. Для описания имитационных моделей на системном уровне (иногда их называют сетевыми имитационными моделями - СИМ) чаще используют языки, ориентированные на события (Симскрипт, SMPL) или процессы (Симула, SOL, GPSS).

Сети Петри

Сети Петри – аппарат для моделирования динамических дискретных систем. Предложен Карлом Адамом Петри в 1962 году. Сеть Петри определяется конечными множествами позиций и переходов P и Т, множествами входных и выходных функций I и O и представляет собой двудольный ориентированный граф, в котором позиции изображаются кружками, а переходы утолщенными черточками; функциям I соответствуют дуги, направленные от позиций к переходам, а функциям О – от переходов к позициям.

Как и в СМО, в сетях Петри вводятся объекты двух типов: динамические – изображаются метками (маркерами) внутри позиций и статические – им соответствуют вершины сети Петри. Распределение маркеров по позициям называют маркировкой. Маркеры могут перемещаться по сети. Каждое изменение маркировки называют событием. Совершению события соответствует срабатывание перехода, при котором маркеры из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно и разновременно при выполнении некоторых условий. Последовательность событий образует моделируемый процесс.

Правило срабатывания переходов: переход срабатывает, если для каждой из его входных позиций выполняется условие , где - число маркеров в i-й входной позиции, - число дуг, ведущих от i-й позиции к переходу; при срабатывании перехода число маркеров в i-й позиции уменьшается на , а в j-й выходной позиции увеличивается на , где - число дуг, связывающих переход с j-й позицией.

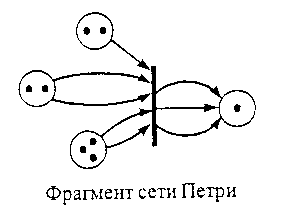
Рис. Фрагмент сети Петри. До срабатывания маркировка (2,2,3,1), после срабатывания (1,0,1,4).

Можно вводить ряд дополнительных правил и условий в алгоритмы моделирования. Задавая продолжительность (задержку) срабатывания перехода, можно моделировать не только последовательность событий, но и привязку ко времени. Полученную модель называю временной сетью Петри.

Если задержки являются случайными величинами, то сеть называют стохастической. В стохастических сетях возможно введение вероятностей срабатывания переходов и вероятностный выбор срабатывающего перехода в конфликтных ситуациях. На рис. 2.3. показан фрагмент сети Петри, с конфликтной ситуацией – маркер р может запустить переход или .

Рис. 2.3. Конфликтная ситуация

Если задержки определяются как функции некоторых аргументов, которыми могут быть количества маркеров в какой-либо позиции, состояния некоторых переходов и т.п., то сеть называют функциональной.

Во многих задачах динамические объекты могут быть нескольких типов с разными алгоритмами поведения. Их идентифицируют разными цветами маркеров, при этом сеть Петри называется цветной.

В ингибиторных сетях Петри возможны запрещающие (ингибиторные) дуги. Наличие маркера во входной позиции, связанной с переходом ингибиторной дугой, означает запрещение срабатывания перехода.

Пример сети Петри. Требуется описать работу группы пользователей на одной рабочей станции WS.

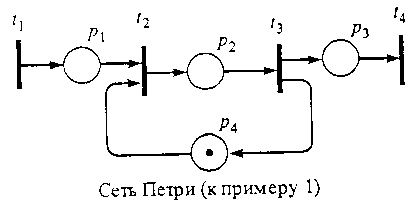
Рис. Сеть Петри для примера.

События: t1 – поступление запроса на использование WS; t2 – занятие станции; t3 – освобождение станции; t4 – выход обслуженной заявки; позиция р4 используется для отображения состояния WS: если в p4 имеется метка, то WS свободна и пришедшая заявка вызывает срабатывание перехода t2; пока эта заявка не будет обслужена, метки в р4 не будет, и пришедшие в р1 запросы вынуждены ожидать срабатывания перехода t3.