54.Геометрические приложения определённого интеграла. Вычисление площади криволинейной трапеции в декартовых координатах и криволинейного сектора в полярных координатах. Дифференциал длины дуги. Вычисление длины дуги при разных способах задания функции.

1. Вычисление площади плоской фигуры

 

1.1. Пусть функция непрерывна и неотрицательна на отрезке [a, b]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции , может быть вычислена по формуле(см. 10.1 рис. 1).

1.2. Если на отрезке [a, b],  непрерывные функции, то площадь фигуры, ограниченной прямыми х = а, x = b, графиками функций вычисляется по формуле(рис. 10).

1.3. Если функция на отрезке [a, b] принимает значения разных знаков, то площадь фигуры, заключенная между кривой и осью, равна (рис. 11).

Вычисление площади в декартовой системе координат.

Мы уже знаем, что, если на [a,b], то равен площади некоторой криволинейной трапеции ( см. п.2.1 )

Площадь области, ограниченной сверху графиком функции y = f(x), снизу графиком функции y = g(x) , справа и слева прямыми x = a и x = b, можно вычислить как разность интегралов, которую можно записать как интеграл от разности:

 (1)

Надо отметить, что эта формула справедлива независимо от знака функций y = f(x) и y = g(x).

55.Понятие кратного интеграла. Геометрический смысл двойного интеграла. Физический смысл тройного интеграла.

56.Понятие криволинейного интеграла по дуге. Геометрический и физический смысл

57. Обыкновенное дифференциальное уравнение, порядок уравнения, решение уравнения, интегральная кривая, общее, частное, особое решения.

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида

F (x, y(x), y '(x), y ''(x),  …  , y⁽ⁿ⁾(x)) = 0,

где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число nназывается порядком уравнения.

 Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество.

Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме:

y⁽ⁿ⁾ = f(x, y, y ',  y '',  …  , y^{(n − 1)}).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия.

 

Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

 

Задачей Коши (или начальной задачей) называется задача отыскания решения y = y(x) уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0,    x>x₀,

удовлетворяющего условиям

y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

 

Условия   y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1} называются начальными данными, начальными условиями или данными Коши.

 

Любое конкретное решение y = φ(x) уравнения n –го порядка F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0, называется частным решением.

 

Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0

называется функция

y = Ф(x,  С₁, С₂, … , С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

1. Ф(x, С₁, С₂,  … , С_n) является решением уравнения при любых допустимых значениях С₁, С₂, … , С_m;

2. для любых начальных данных  y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂,  … , С_n = A_n, такие что решение y = Ф(x, A₁, A₂,  …, A_n) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С₁,  С₂,  ..., С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

58.Уравнение первого порядка, разрешённое относительно производной. Область определения уравне-ния. Поле направлений. Изоклины. Построение интегральной кривой с помощью поля направлений

Уравнение

F(x, y, y ') = 0,

где y = y(x) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.

 

Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y'(x)) ≡ 0 для всех x из (a,b) .

 

График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.

 

Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.

Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x₀) = y₀, называется задачей Коши (или начальной задачей).

Условие y(x₀) = y₀ — начальное условие.

 

Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.

 

Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.

 

Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называется частным интегралом уравнения.

 

Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:

 

Уравнения первого порядка часто записывают в дифференциальной форме:

M(x, y)dx + N(x, y)dy = 0.

Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y) .

Особенности дифференциальных уравнений первого порядка

При решении уравнений первого порядка функцию y и переменную x следует считать равноправными. То есть решение может быть в виде y(x) так и в виде x(y).

Дифференциальные уравнения первого порядка, разрешенные относительно производной

Уравнения с разделяющимися переменными 

Уравнения, приводящиеся к уравнениям с разделяющимися переменными 

Однородные уравнения 

Уравнения, приводящиеся к однородным 

Обобщенные однородные уравнения 

Линейные дифференциальные уравнения

• Линейное по y

• Линейное по f(y)

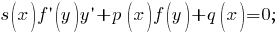
• Линейное по x 

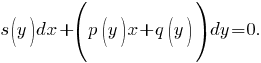
• Линейное по f(x) 

Уравнения Бернулли 

Уравнения Риккати 

Уравнения Якоби 

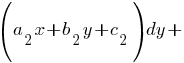
Уравнения в полных дифференциалах  при условии

Интегрирующий множитель  Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то следует попытаться найти интегрирующий множитель, чтобы свести его к уравнению в полных дифференциалах.