Структуры и алгоритмы обработки данных

Практическое занятие № 2.

Программирование алгоритма сжатия данных хаффмана

Учебные вопросы:

1. Реализация алгоритма компрессии

2. Реализация алгоритма декомпрессии

Учебные и воспитательные цели:

1. Совершенствование навыков разработки программ в среде программирования MS Visual C++

2. Получение начальных навыков работы с алгоритмами сжатия данных

Время на выполнение работы: 2 часа

Подготовка к выполнению работы:

1. Изучить рекомендованную литературу (методы кодирования данных, алгоритм Хаффмана).

2. Изучить материал настоящего руководства.

Материалы для подготовки к занятию:

1. Конспект лекций

2. [2] c.237 – 245

Теоретические сведения

Несмотря на наличие запоминающих устройств большой ем­кости и большие скорости передачи данных, проблема сжатия данных остается актуальной. Решению этой проблемы уделяется достаточно серьезное внимание. Разработано много способов сжатия данных различных видов: текстовых, графических и т.д.

Кратко рассмотрим некоторые алгоритмы, применяемые к бай­товому представлению данных.

При рассмотрении алгоритма сжатия нас интересуют такие его характеристики, как:

• коэффициент сжатия данных;

• ориентирован­ность на исходные данные;

• временная сложность алгоритма;

• по­требность в дополнительной памяти.

Методы сжатия можно разбить на два класса:

• методы, ориентированные на конкретную структуру или содержимое дан­ных и разрабатываемые в расчете на конкретные приложения;

• методы, которые используются во многих приложениях.

Методы сжатия первого класса рассмотрим на примере сжа­тия данных в телефонном справочнике о жителях населенного пункта.

Пусть информация о жителе представляется в виде записи, имеющей структуру с элементами:

• фамилия, имя, отчество,

• дата рождения,

• место рождения,

• номер телефона,

• адрес (улица, номе­ра дома и квартиры).

Для сжатия данных такого вида можно применить несколько способов.

Переход от естественных обозначений к более компактным представлениям. Данные, представленные в виде, удобном для чтения человеком, можно сжать за счет другого, более компакт­ного представления.

Дату мы привыкли представлять в символь­ном виде, например 12 апр 1961, 12.04.1961, 12/04/1961. При этом каждая дата будет записываться в строку длиной 11 или 12 байт. Если удалить все разделительные символы, то в самой краткой форме: 12041961 — она займет 9 байт. Если же эту строку преоб­разовать в число, то для ее хранения в памяти достаточно 4 байт. Таким образом, строка символов длиной 9 байт сжимается до 4 байт. Аналогичным способом номера телефонов также могут быть сжаты до 4 байт.

Имеется другой способ представления дат как общее число дней, прошедших к данной дате, считая от какой-либо исходной, фиксированной для данного приложения даты. Можно также каждый элемент даты представлять определенным числом бит: день — 5 битами, месяц — 4 битами и год — 11 бита­ми, тогда дату можно упаковать в 20 бит и поместить в 3 байта.

Кодирование элементов, имеющих одинаковые значения. Обыч­но в населенном пункте встречается много однофамильцев, а чис­ло различных фамилий и имен ограничено. Наиболее распрост­раненные 256 имен можно закодировать одним байтом, а имена, не попавшие в этот перечень, представлять полностью. Таким же способом можно закодировать названия улиц. Фамилии отли­чаются большим разнообразием, чем имена. Учитывая, что фа­милии часто образованы от имен, ту часть фамилии, которая совпадает с именем, можно заменить кодом имени.

Этот способ сжатия данных требует наличия кодовой таблицы как при кодировании, так и при декодировании данных.

Сжатие упорядоченных данных. Поскольку телефонный справочник лексикографически упорядочивается по фамилиям, то начальные символы фамилий в соседних элементах часто совпадают. Тогда в последующих элементах справочника вместо начальных символов фамилий в первом байте можно указать число совпадающих символов, например:

Исходное представление	Сжатое представление
Иванов	Иванов
Иванов	6
Ивановский	6ский
Иванченко	4ченко
Ивашкин	3шкин
Ивашов	3шов
Ивлиев	2лиев

При таком кодировании не требуется дополнительной таблицы, но последующие записи оказываются зависимыми от предыдущих, поэтому алгоритмы добавления и удаления элементов в справочнике усложняются.

Следующие алгоритмы сжатия применимы во многих приложениях.

Групповое кодирование. Это один из самых старых и простых алгоритмов сжатия данных.

Сжатие происходит за счет того, что в исходных данных встречаются цепочки одинаковых байтов. Замена их на пары <счетчик, значение> уменьшает избыточность данных. Дополнительной памяти алгоритм не требует, выполня­йся быстро за один проход. При передаче данных этот способ применяется и для сжатия цепочки одинаковых битов.

Кодирование одинаковых цепочек байтов. Сжатие осуществля­ется за счет повторяющихся одинаковых цепочек байтов. Алго­ритмы этого способа различаются методами поиска повторяю­щихся цепочек (методами поиска подстроки в строке) и значительно сложнее алгоритмов группового кодирования.

Алгоритм Хаффмана. Является одним из классических алгорит­мов. Алгоритм использует частоту (вероятность) появления одина­ковых элементов (символов) в данных.

Элементы входного потока, которые встречаются чаще (имеют большую вероятность), кодиру­ются цепочкой битов меньшей длины, а встречающиеся редко — цепочкой большей длины. Алгоритм выполняется за два прохода: сбор статистики и непосредственное кодирование. Алгоритм тре­бует наличия кодовой таблицы. Таблицы могут быть постоянными или создаваться по результатам сбора статистики при первом про­ходе. Средняя длина кода элемента определяется выражением

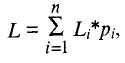
где п — число различных элементов в сжимаемых данных;

p_i — вероятность появления i-го элемента;

L_i — длина кода i-го элемента.

Коды Хаффмана обладают двумя важными свойствами.

Во-первых, коды Хаффмана являются двоичными кодами с минимальной средней длиной.

Во-вторых, коды Хаффмана облада­ют префиксным свойством. Это означает, что ни один код в по­лученном множестве кодов не имеет префикса другого кода. По­этому обычным сканированием строки с кодами Хаффмана мож­но выделить каждое следующее закодированное значение в силу уникальности префикса. Например, пусть некоторое сообщение включает только символы а, в, г, д, о с вероятностями появления их 0.12, 0.40, 0.15, 0.08, 0.25, и они закодированы последователь­ностями битов: а — 000, в — 11, г — 01, д — 001, о — 10 соответ­ственно. Тогда двоичная последовательность битов «1110001000» будет соответствовать исходной последовательности символов «вода». Действительно, сканируя двоичную последовательность, выделяем префиксы (коды): 11 (в), 10 (о), 001 (д) и 000(a).

Недостатком кодов Хаффмана является то, что из-за перемен­ности их длины при декодировании для выделения очередного элемента требуются дополнительные затраты времени. Кроме того, потеря или изменение одного бита в битовой последова­тельности может привести к печальным последствиям.

Как видим, для реализации алгоритма Хаффмана необходи­мо построить кодовую таблицу. Она используется и для кодиро­вания исходного текста, и для декодирования. Элементами таб­лицы являются структуры вида: <символ>, <код>, <длина кода>. Следует выбирать таблицу, наиболее соответствующую характе­ристикам конкретных кодируемых данных.

Существует много различных модификаций префиксных ко­дов переменной длины. Известен алгоритм построе­ния таблицы с помощью бинарного дерева Хаффмана. Существуют таблицы кодирования с длинами кодов от 1 до 16 бит и от 1 до 17 бит. Воспользуемся одной из них для кодирования тек­ста, включающего строчные буквы русского алфавита, пробелы, запятые, точки с запятой и точки, всего 36 символов. Так как кодируется произвольный текст, статистические характеристики которого неизвестны, символы в кодовой таблице также распо­ложены в произвольном порядке.

Из-за того, что коды имеют переменную длину, функции ко­дирования оперируют не только символами, но и частями их, т.е. битами, что демонстрирует приведенная ниже программа.

В первое слово закодированного текста помещается длина исходного текста в байтах, она используется в функции декоди­рования.

В файле включения находятся функции кодирования и декодиро­вания, а также таблица кодирования и переменные.