Робота 7. Дослідження якісних показників роботи лінійних систем автоматичного регулювання

7.1. Мета роботи

Ознайомитися з методами оцінки якісних показників роботи систем автоматичного керування, навчитись розраховувати оптимальні значення уставок регуляторів та експериментально дослідити вплив коефіцієнтів передачі регуляторів на якісні показники регулювання в лінійній системі на основі квадратичної інтегральної оцінки якості.

7.2. Загальні відомості

Для повноцінного функціонування система автоматичного регулювання повинна бути не тільки стійка, але й відповідати вимогам щодо якісних показників роботи. Під якістю регулювання розуміють набір показників, які характеризують динаміку перехідного процесу і точність роботи системи в усталеному режимі.

Найчастіше оцінку якості регулювання здійснюють на основі перехідної характеристики системи. Показники якості регулювання, визначені за перехідною характеристикою, називають прямими показниками. Існують також непрямі наближені методи оцінки якості регулювання. До них належать кореневі, частотні та інтегральні критерії якості.

Серед прямих показників якості виділяють такі: перерегулювання, час регулювання, коливальність та усталену похибку.

Під перерегулюванням розуміють максимальне відхилення регульованої величини від її усталеного значення в процесі регулювання (рис.7.1). У відносних одиницях перерегулювання визначається формулою

. /7.1/

Час регулювання визначається інтервалом від початку перехідного процесу до моменту, коли відхилення регульованої величини від її усталеного значення за абсолютною величиною стає меншим за деяку наперед задану величину . Величина cкладає , як правило, 5% від усталеного значення регульованої величини.

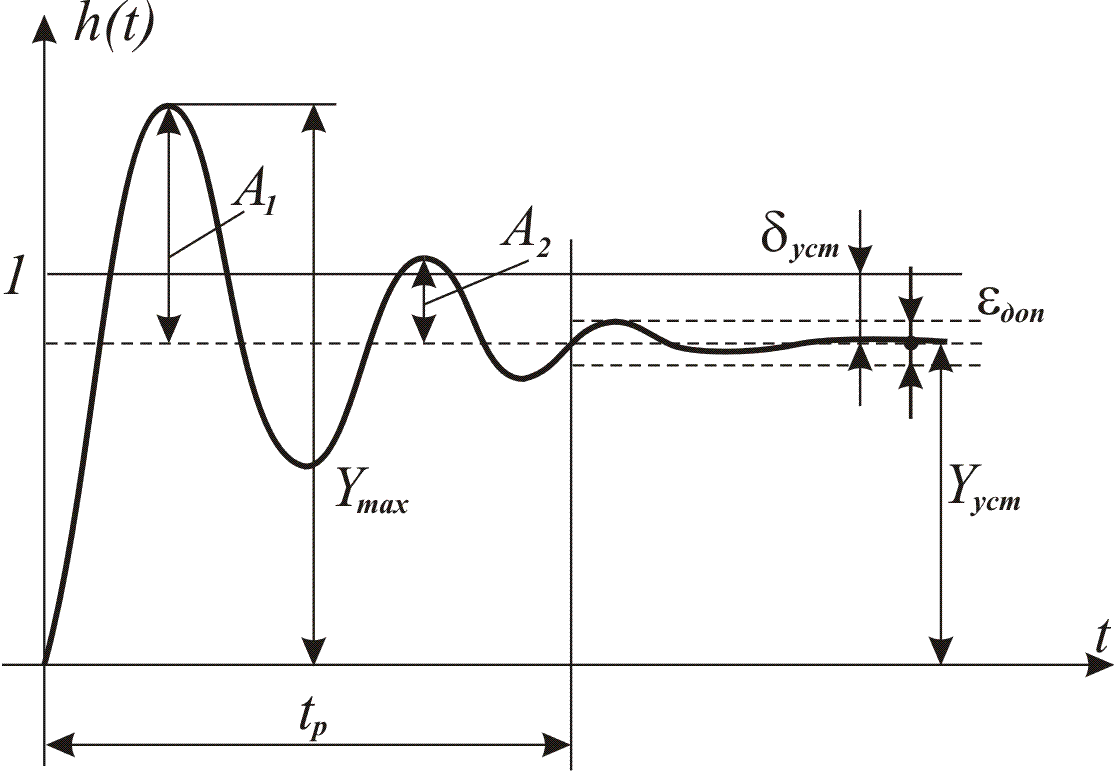
Рис.7.1. Типова перехідна характеристика лінійної системи.

Коливальністю перехідного процесу називають відношення амплітуд коливань двох послідовних періодів:

. /7.2/

На практиці коливальність визначають кількістю повних коливань регульованої величини за час регулювання. Перехідний процес вважається задовільним, якщо число повних коливань за час регулювання не перевищує 2…3.

Точність в усталеному режимі прийнято оцінювати величиною усталеної похибки

. /7.3/

Величину усталеної похибки легко знайти з передаточної функції похибки

. /7.4/

Передаточна функція похибки каналу керування (завдання) знаходять за формулою

, /7.5/

де - передаточна функція розімкненої системи.

Система автоматичного регулювання називається астатичною, якщо при ступінчастій вхідній дії усталена похибка . При довільному вхідному сигналі точність системи в усталеному режимі залежить від порядку астатизму. У загальному випадку система є астатичною -го порядку, якщо передаточна функція похибки має нуль -го порядку, тобто коли передаточну функцію можна представити у формі

. /7.6/

Порядок астатизму систем автоматичного керування визначається числом інтегруючих ланок, включених в контур регулювання.

Інтегральні оцінки якості дають загальну оцінку швидкості затухання та відхилення регульованої величини в процесі регулювання.

Вони діляться на лінійні і квадратичні. До коливних затухаючих перехідних процесів можуть бути застосовані лише квадратичні інтегральні оцінки якості. Найпростіша квадратична оцінка якості керування є функціоналом від динамічної помилки системи і визначається за формулою

/7.7/

Динамічна похибка виражає миттєве відхилення регульованої величини від її усталеного значення

/7.8/

Інтегральна оцінка може бути виражена через зображення Лапласа від динамічної похибки системи

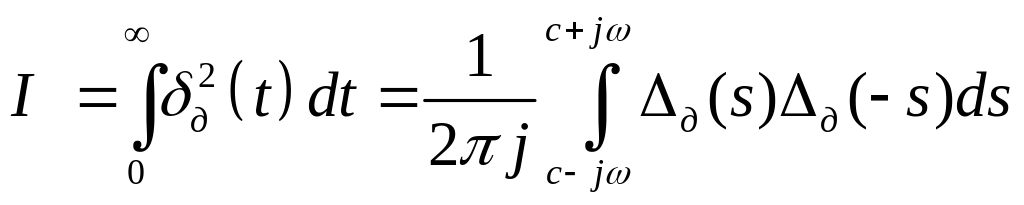/7.9/

Для визначення квадратичної оцінки за зображенням динамічної похибки на практиці використовують формулу Рейлі, яку отримують з /7.9/ шляхом заміни

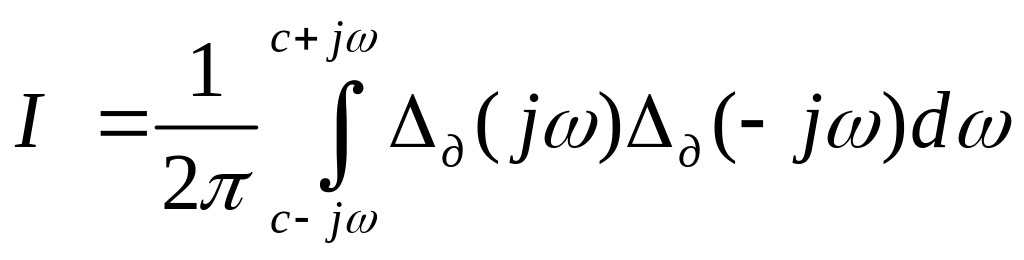/7.10/

Розроблені різні методи обчислення квадратичної оцінки на основі формули Рейлі. Зокрема, Мак–Леном отримані вирази для квадратичних оцінок якості керування для випадку, коли зображення динамічної похибки системи є дробово-раціональною функцією

/7.11/

зі степенем полінома чисельника меншим на одиницю від степені полінома знаменника.

За методом Мак–Лена спочатку знаходять зображення динамічної похибки системи за формулою

, /7.12/

де - передаточна функція замкненої системи, - зображення вхідної дії.

За виглядом зображення динамічної похибки вибирають вираз для визначення квадратичної оцінки якості. Якщо зображення динамічної похибки системи третього порядку має вигляд

, /7.13/

то квадратичну оцінку якості знаходять за формулою

. /7.14/

Інтегральні оцінки якості використовуються для знаходження оптимальних настроювальних параметрів системи. Наприклад, оптимальне значення коефіцієнта передачі регулятора при якому інтегральна оцінка якості приймає мінімальне значення знаходять з умови

. /7.15/

Аналогічно можна знайти оптимальне значення іншого параметра при фіксованому значенні вже визначеного параметра.

В роботі досліджується якість керування системи автоматичного регулювання з І- та ПІ- регуляторами. При цьому модель об’єкта керування складається з послідовного з’єднання двох аперіодичних ланок.

Передаточна функція об’єкта регулювання

. /7.16/

Оскільки, передаточна функція розімкненої системи дорівнює добутку передаточних функцій регулятора і об’єкта

, /7.17/

то при використанні І-регулятора з передаточною функцією

/7.18/

передаточна функція розімкненої системи має вигляд

. /7.19/

Відповідно, передаточна функція замкненої системи з І-регулятором

. /7.20/

При одноступінчастому вхідному сигналі зображення вхідної величини

. /7.21/

За цих умов зображення за Лапласом від динамічної помилки системи з І регулятором

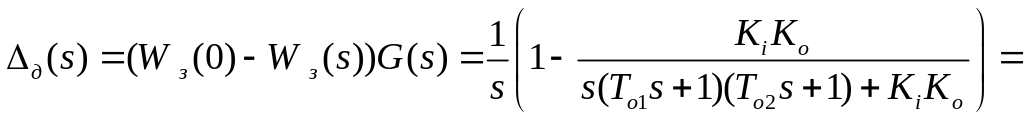
. /7.22/

Прирівнявши коефіцієнти при відповідних степенях у виразах /7.13/ і /7.22/ отримаємо , , , , , ,

Підставивши значення коефіцієнтів і у формулу /7.14/, знаходимо

Для даної системи умова /7.15/ має вигляд:

Після підстановки в це рівняння числових значень всіх коефіцієнтів, отримуємо вираз для визначення оптимального коефіцієнта , що забезпечує мінімум інтегральної квадратичної оцінки якості системи з I- регулятором. Для випадку , одержимо

/7.23/

Аналогічно знаходять вираз для визначення оптимального значення коефіцієнта передачі інтегральної частини ПІ-регулятора. Для випадку ,

/7.24/

де - коефіцієнт пропорційної частини ПІ-регулятора.