3.2. Распределение рэлея

Джон Уильям Стретт, после смерти отца - лорд Рэлей, более правильно - Рейли, (по-английски-Rayleigh), выдающийся английский физик (1842-1919), один из основоположников теории колебаний, Нобелевский лауреат 1904 года по физике, предложил для описания случайных величин следующие формулы:

Вероятность безотказной работы:

р(t) = Exp(-аt²). (3-5)

Плотность распределения:

f(t) = q(t) = (-2аt)[-Exp(-аt²)] = 2аt Exp(-аt²). (3-6)

Интенсивность отказов:

(t) = 2аt Exp(-аt²)/Exp(-аt²) = 2аt. (3-7)

Задача определения CНДО в данном случае представляет собой сложную задачу взятия интеграла от ВБР по выражению (3-5). Поэтому без вывода

Т²_ср = /4а или Т_ср = √/4а . (3-8)

Как видно из выражения (3-7), при распределении Рэлея интенсивность отказов растет пропорционально времени, что позволяет этому закону хорошо описывать любые деградационные явления – усталость металла, старение

изоляции, уход параметров за допустимые пределы и других подобных явлений.

3.3. Обобщенный двухпараметрический закон распределения вейбулла

Где эти два параметра? Что обобщает этот закон? Выражение закона Вейбулла для ВБР:

р(t) = Exp(-аt^b), (3-9)

где а и b – параметры распределения.

При значении параметра b=1 получаем выражение экспоненциального закона распределения, а при b=2 - закона Рэлея. Закон распределения Вейбулла включает в себя (обобщает) эти два закона в качестве частных случаев.

Плотность распределения при этом законе

f(t) = q(t) = [1-Exp(-аt^b)] =

= (-а)bt^b-1[-Exp(-аt^b)] = аbt^b-1Exp(-аt^b). (3-10)

Интенсивность отказов имеет вид

(t) = аbt^b-1Exp(-аt^b)/Exp(-аt^b) = аbt^b-1. (3-11)

Рассмотрим влияние параметра b на вид зависимостей от времени интенсивности отказов . Подставляя в (3-11) b=1, получим (t)=а=Const, а при b=2 - (t)=2аt, то есть уравнения прямых линий. Взяв в качестве b1, значение 0.5, получим (t) = 0.5/√t, графиком чего будет кривая, похожая на гиперболу. При 1b2, например, 1.5, получаем (t)=1.5аt^0.5. Эта кривая соответствует функции квадратного корня. И, наконец, при b2, например, b = 3, получаем (t)=3аt², графиком чего является парабола. Графики зависимостей (t) при всех возможных вариантах параметра b представлены на рисунке 3.1.

Таким образом, закон распределения Вейбулла позволяет описывать практически любые распределения НДО. Параметр b является коэффициентом формы кривых (t) и р(t).

Рис. 3.1.

Интенсивности отказов в зависимости от параметра b

Вид зависимостей р(t) (рис. 3.2) меняется не столь резко, как (t), так согласно общей формуле ВБР, она является показательной функцией независимо от закона распределения. При b1 график р(t) похож на график экспоненты (b=1), При всех b1 эта кривая имеет точку перегиба. Степень изогнутости кривой р(t) увеличивается с ростом параметра b.

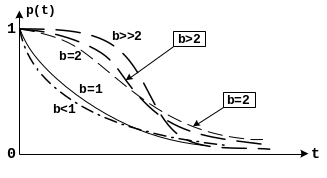
Рис.3.2.