7 Приклад розв’язання деяких типових завдань

Приклад розв’язання завдання 1. Припустимо, задані універсальна множина U та чотири її підмножини А, В, C, D.

U = {1, 2, 3, ... , 60};

A={a  U | a=p · i};

B={b  U | b=q · i};

C={c  U | c=r · i};

D={d  U | d=s · i};

i=1,2,3,...n, p=5, q=8, r=6, d=3.

Якщо i=1,...,12, то А = {5 · i} = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60}.

Якщо i=1,..., 7, то B = {8 · i} = {8, 16, 24, 32, 40, 48, 56}.

Якщо i=1,...,10, то C = {6 · i} = {6, 12, 18, 24, 30, 36, 42, 48, 54, 60}.

Якщо i=1,...,20, то D = {3 · i} = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60}.

Для відображення множин за допомогою кругів Ейлера (рис. 7.1) знайдемо вирази A  B, A  C, A  D, B  C та B  D.

Рисунок 7.1

1) A  B = {40};

2) A  C = {30, 60};

3) A  D = {15, 30, 45, 60};

4) B  C = {24, 48};

5) B  D = {24, 48}; CD.

Приклад розв’язання завдання 2. У табл. 7.1 записані значення 10 булевих функцій f(x,y,z).

Таблиця 7.1

X	Y	Z	F
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

За таблицею значень булевої функції записати її ДДНФ і ДКНФ, визначити, чи є дана функція самодвоїстою, лінійною, яка зберігає 0 та зберігає 1, чи являє ця функція функціонально повний набір? Спростити отримані ДДНФ, використовуючи тотожності булевої алгебри.

З табл. 7.1 отримаємо ДДНФ:

Спростимо ДДНФ:

З табл. 7.1 отримаємо ДКНФ:

Спростимо ДКНФ:

Перевіряємо, чи лінійна функція. Для цього знайдемо полiном Жегалкiна для цiєї функцiї.

f(x,y,z) = ( y  1 ) z  y ( z  1 )  z ( y  1 ) y ( z  1 ) = yz  z  yz  y 

 yz ( yz  y  z  1 )= yz  z  yz  y  yz  yz  yz  yz = y  z

Оскільки поліном Жегалкiна не має кон’юнкції змінних, то функція є лiнiйною.

Перевіримо функцію на монотонність. Для того, щоб булева функція F(x,y,z) була монотонною, треба, щоб виконувалася умова: якщо А, В – набори значень змінних булевої функції та якщо A B, то F(A) F(B).

(1,1,1) (0,0,0);

(1,1,1) (0,0,1);

(1,1,1) (0,1,0);

(1,1,1) (1,1,1);

(0,1,0) (0,0,0);

(0,0,1) (0,0,0);

f(1,1,1) f(0,0,0);

f(1,1,1) f(0,0,1).

Робиться висновок: функцiя не є монотонною.

Функцiя зберiгає 0, оскільки f(0,0,0) = 0.

Функцiя не зберiгає 1, оскільки f(1,1,1) = 0.

Сукупнiсть властивостей функцiї f(x,y,z) наведено у табл. 7.2.

Таблиця 7.2

Формула функцiї f(x,y,z)	Властивостi
	не збе-рігає 0	Не збе-рігає 1	не само-двоїста	нелі-нійна	немоно-тонна
		*	*		*

Умови теореми Поста не виконуються, тому функція f(x,y,z) не є функціонально повним набором.

Приклад розв’язання завдання 3. У табл. 7.3 наведені значення двох булевих функцій. Визначити, чи є такий набір функцій функціонально повним.

Таблиця 7.3

Параметр			Набір
x	y	z	f1	f2
0	0	0	1	0
0	0	1	0	1
0	1	0	1	0
0	1	1	0	0
1	0	0	1	1
1	0	1	0	1
1	1	0	1	0
1	1	1	0	1

Перевіримо заданий набір на вміст класів Поста:

1) збереження 0 та 1. Функція f₁ не зберігає 0 та не зберігає 1, тому що f₁(0,0,0)0 та f₁ (1,1,1)1;

2) перевіримо функції на монотонність. Функція f₁ не є монотонною, оскільки з того, що (1,1,1) ≥(1,1,0) не витікає, що f(1,1,1)≥f(1,1,0);

3) перевіримо функції на самодвоїстість (табл. 7.4). Для наведених функцій справедливі тотожності f₁=f₁^*; f₂=f₂^*. Отже, набір функцій f₁ та f₂ не містить жодної несамодвоїстої функції.

Отже, зазначений набір булевих функцій не повний. На лінійність перевірку можна не проводити.

Приклад розв’язання завдання 4. За допомогою метода Квайна – Мак-Класкі мінімізувати ДДНФ булевої функції, яка задана номерами конституент одиниці, що закодовані десятковими еквівалентами: 0,1,2,3,5,7,8,10,11,12,13.

Таблиця 7.4

Параметр			Набір
x	y	z	f1	f1*	f2	f2*
0	0	0	1	1	0	0
0	0	1	0	0	1	1
0	1	0	1	1	0	0
0	1	1	0	0	0	0
1	0	0	1	1	1	1
1	0	1	0	0	1	1
1	1	0	1	1	0	0
1	1	1	0	0	1	1

У табл. 7.5 запишемо конституенти одиниці даної функції у вигляді двійкових кодів у другий стовпчик. У третій стовпчик запишемо відповідні конституенти одиниці функції f(x,y,z,t).

Таблиця 7.5

Номер	Набір значень змінних x, y, z, t	Конституенти одиниці функції f(x,y,z,t)
0	0 0 0 0
1	0 0 0 1
2	0 0 1 0
3	0 0 1 1
5	0 1 0 1
7	0 1 1 1
8	1 0 0 0
10	1 0 1 0
11	1 0 1 1
12	1 1 0 0
13	1 1 0 1

Відповідно до методу здійснимо такі кроки:

1. Згрупуємо двійкові коди імплікант з однаковою кількістю одиниць. Назвемо кількість одиниць m індексом групи. Упорядкуємо групи в порядку зростання індексу m.

2. Починаючи з т = 0, зробимо порівняння кожного двійкового коду в групі з індексом т з кожним кодом з групи з індексом т+1. Якщо порівнювані двійкові коди відрізняються тільки в одному розряді, то у наступний стовпчик таблиці запишемо відповідний їм двійковий код з порожньою позначкою «-» на місці зазначеного розряду. Напроти кожного нового коду запишемо номери кодів двох імплікант, які брали участь у порівнянні, i у наступному стовпчику ці імпліканти позначимо знаком «V», оскільки вони не є простими імплікан­тами. Всі коди, які залишилися непозначеними знаком «V», відповідають простим імплікантам, тому позначимо їх знаком «X».

3. Якщо серед знов одержаних імплікант є однакові, то з них для подальшого використання залишаємо тільки одну.

4. Повторюємо кроки 1-3 доти, доки існує можливість одержувати нові коди імплікант.

Результат виконання описаних кроків наведено у табл. 7.6. Спочатку заповнюємо три стовпчики нульового циклу: т (десятковий індекс групи), двійковий код імпліканти, номер імпліканти. Імпліканти ділимо на групи за значенням т.

Таблиця 7.6

Потім здійснимо порівняння першої імпліканти з групи т = 0 (імпліканта 0000) з першою імплікантою з групи т = 1 (імпліканта 0001). Вони відрізняються тільки в одному розряді, тому робимо їх склеювання та одержуємо нову імпліканту з кодом 000-. Записуємо даний код у стовпчик коду імпліканти циклу 1, а напроти імплікант 0000 i 0001 ставимо позначки «V», оскільки вони не є простими. Їх номери вказуємо поряд з кодом 000-. Потім порівнюємо імпліканту 0000 з другою імплікантою з групи т=1 – імплікантою 0010 тощо.

Коли порівняння всіх кодів імплікант стовпчика «цикл 0» завершено, аналізуємо стовпчик виду імпліканти. Напроти Всіх імплікант ставимо позначення «V», оскільки в циклі 0 кожна імпліканта припускає склеювання i не є простою. Далі розділяємо на групи т=0, т=1 i m=2 коди імплікант циклу 1. Потім попарно порівнюємо ці імпліканти й одержуємо стовпчик коду імплікант «цикл 2». Коди, що містять знаки «-», можуть утворювати нові імпліканти, тільки якщо вони містять знаки «-» в одних i тих самих розрядах. Закінчивши порівняння, виділяємо прості імпліканти у стовпчику «вид» «циклу 1», які не мають позначки «V», i позначаємо їх «X». У стовпчику «код» «циклу 2» є однакові імпліканти, тому довільно викреслюємо один з однакових рядів, щоб кожна імпліканта зустрічалася тільки один раз. Порівнюючи коди імплікант у «циклі 2», приходимо до висновку, що методом склеювання з них неможливо одержати нові імпліканти. Всі коди циклу 2 відповідають простим імплікантам, отже, побудову таблиці завершено.

Для знаходження тупикових ДНФ побудуємо імплікантну таблицю, в рядках якої розташовуємо двійкові коди, що відповідають простим імплікантам, а в стовпчиках – коди, що відповідають конституентам одиниці. Якщо двійковий код рядка є частиною коду стовпчика (позиції із знаком «-» не порівнюються), то у відповідну клітинку таблиці записуємо знак «*» (табл. 7.7).

Таблиця 7.7

Позначимо стовпчики таблиці, які містять по одному знаку «*». Відповідні їм прості імпліканти є диз'юнктивними ядрами. Викреслюємо рядки таблиці, що відповідають ядрам, i стовпчики, покриті ядрами, як зображено у табл. 7.8.

Таблиця 7.8

Одержуємо спрощену імплікантну таблицю (табл. 7.9).

Таблиця 7.9

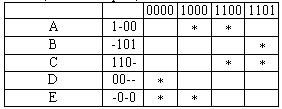
Тепер знайдемо всі тупикові ДНФ функції f(x,y,z,t) i оберемо з них мінімальну. Згідно з методом Петрика, кожній з імплікант таблиці приписуємо літерне позначення i записуємо формулу покриття конституент одиниці простими імплікантами.

Конституента одиниці з кодом 0000 може бути покрита імплікантою D або імплікантою Е, тобто диз'юнкцією: DE. Конституента одиниці з кодом 1000 може бути покрита імплікантою А або імплікантою Е: AE.

Аналогічно 1100 може бути покрита AС, а 1101 – диз'юнкцією BС. Таким чином, покриття конституент одиниці спрощеної імплікантної таблиці функції f(x,у,z,t) простими імплікантами можна записати у вигляді формули покриття:

(DE)(AE)(AС)(BС).

Якщо у цій формулі розкрити дужки, то отримаємо символьне зображення вcix можливих наборів простих імплікант для тупикових ДНФ, що не включає диз'юнктивні ядра:

(DE)(AE)(AС)(BС)=(DAEADEE)(ABCBACC)=DABEABDEA EABDACBEACBDECBECBDACEACDEACEACDACEACDEC EC=ABDABEABDEABCDABCEACEBCDEACDEACDCDECBE EC

В одержаній формулі кожна кон'юнкція літерних позначень відповідає набору імплікант у деякій тупиковій ДНФ, до якої обов'язково входять також диз'юнктивні ядра. Для того щоб одержати мінімальну ДНФ, необхідно вибрати набір з мінімальною кількістю імплікант (у даному прикладі це ЕС) i додати імплікантні ядра (0--1, -01-). Одержуємо мінімальну ДНФ вихідної функції:

МДНФ .

Таким чином, за допомогою метода Квайна – Мак-Класкі одержана мінімальна ДНФ функції f(x, у, z, t), яка містить лише 4 елементарні кон'юнкції замість 11 конституент одиниці ДДНФ.

Приклад розв’язання завдання 5. Спростити за допомогою карт Карно функцію .

Побудуємо карту Карно для цієї функції (рис. 7.2).

Рисунок 7.2

Запишемо мінімальну ДНФ, об’єднавши диз’юнкцією прості імпліканти A, B, C, D відповідно:

Таким чином одержуємо мінімальну ДНФ:

Приклад розв’язання завдання 6. За мінімальною ДНФ побудувати перемикальний ланцюг у базисі ТА-НІ (И-НЕ).

Перетворимо формулу за законом де Моргана:

.

Використовуючи логічні елементи „НЕ” та „І-НЕ”, формуємо супер­позицію, що відповідає даній функції. Одержаний логічний ланцюг зображено на рис. 7.3.

Рисунок 7.3

Приклад розв’язання завдання 7. Визначити за допомогою таблиць істинності, до яких висловлювань (Істинне, Хибне, ні те, ні інше) відносяться формули: (РQ)QР і (РQ)QР.

Побудуємо таблиці істинності для функцій (РQ)QР і (РQ)QР (табл. 7.10).

Таблиця 7.10

P	Q	PQ	Q	(РQ)Q	Р	(РQ)QР	PQ	(РQ) QР
І	І	І	Х	Х	Х	І	І	Х
І	Х	Х	І	Х	Х	І	Х	Х
Х	І	І	Х	Х	І	І	І	Х
Х	Х	І	І	І	І	І	І	Х

Табл. 7.10 показує, що (РQ)QР істинна при всіх інтерпретаціях. Отже, (РQ)QР істиннісне висловлювання.

Ми можемо також довести істинність формули шляхом перетворення її у кон’юнктиву нормальну форму:

((РQ)Q)Р=((РQ)Q)Р=((РQ)Q)Р= =((РQ)(QQ))Р=((РQ)0)Р=(РQ)Р=(РQ)Р==(QР)Р=Q(РР)=Q1=1

Таким чином, ((РQ)Q)Р істиннісне висловлювання.

Розглянемо формулу (РQ)QР. З табл. 7.10 робимо висновок, що (РQ)QР хибне висловлювання, оскільки (РQ)QР хибна у кожній інтерпретації.

Можливо також довести хибність формули (РQ)QР шляхом її перетворення у диз’юнктивну нормальну форму:

(РQ)QР=(РQ)QР=(РQР)(QQР)=00=0

Таким чином, (РQ)QР – хибне висловлювання.

Приклад розв’язання завдання 8. Неорiєнтований мультиграф з 10 вершинами заданий матрицею сумiжностi. Деякi елементи цiєї матрицi R_mn, що позначенi коефiцiєнтами m та n, наведенi в табл. 7.11.

Таблиця 7.11

m	1	1	2	1	2	3	3	4	5	6	7	8	8
n	3	2	5	4	7	7	8	6	6	8	8	2	9
Rmn	3	1	2	3	2	2	3	1	2	3	2	0	2

Необхідно:

• побудувати повну матрицю суміжності,

• діаграму графа та матрицю iнциденцiї;

• знайти у графi ейлерів та (або) гамiльтонів цикли, якщо вони є;

• визначити числові характеристики графа: хроматичне число, реберне хроматичне число, цикломатичне число;

• побудувати деяке остовне дерево графа;

• побудувати базис розрiзiв графа, базис циклів графа.

Добудовуємо матрицю суміжності (табл. 7.12).

Таблиця 7.12

m n	1	2	3	4	5	6	7	8	9
1	0	1	3	3	0	0	0	0	0
2	1	0	0	0	2	0	2	0	0
3	3	0	0	0	0	0	2	3	0
4	3	0	0	0	0	1	0	0	0
5	0	2	0	0	0	2	0	0	0
6	0	0	0	1	2	0	0	3	0
7	0	2	2	0	0	0	0	2	0
8	0	0	3	0	0	3	2	0	2
9	0	0	0	0	0	0	0	2	0

З побудованої матрицi сумiжностi видно, що граф матиме 26 ребер і 9 вершин. З таблицi можна побудувати діаграму графа та його матрицю iнциденцiї.

Гамiльтонів цикл відсутній, оскільки граф має точку зчленення V₈. Число компонент зв’язності – 1.

Визначимо хроматичне, реберне хроматичне та цикломатичне числа, для чого зробимо розфарбування вершин та ребер графа. Розфарбуємо вершини графа. Визначимо ступені усіх вершин.

deg v1=7; deg v2=5; deg v3=8;

deg v4=4; deg v5=4; deg v6=6;

deg v7=6; deg v8=10; deg v9=2.

Вершина v₈ має найбільший ступінь. Присвоюємо їй колір 1. Також колір 1 присвоюємо вершинам v₁ та v₅, оскільки вони не суміжні з вершиною v₈ і не суміжні між собою. Обираємо вершину з найбільшим ступенем з тих, що залишилися не розфарбованими. Це вершина v₃. Присвоюємо їй колір 2. Також колір 2 присвоюємо вершинам v₆, v₂ та v₉. Вершини v₇, v₄ та v₅ отримають колір 3. Таким чином, вершини наведеного графа можна розфарбувати у 3 кольори. Отже, хроматичне число h(G)=3. Аналогічно знаходимо реберне хроматичне число H(G)=10.

Для визначення цикломатичного числа застосуємо формулу знаходження цикломатичного числа: (G)= m-n+р=26-9+1=18.