Для мережі, яку наведено на рисунку 3.1,

, або

Далі визначають незалежні полігони і складають схему мережі (рисунок 3.1), на якій вказують номери полігонів, марок і вузлових реперів, номери ходів, довжи­ни ходів в км, або число станцій і перевищення. Спочатку нумерують замкнені, а потім розімкнені полігони, останні “добудовують” до замкнених полігонів.

Розімкнені полігони вибирають так, щоб кожний полігон утримував менше число ходів для зменшення в подальшому обсягів об­числювальних робіт. Для мережі, наведеної на рисунку 3.1, по­лігон ІІІ вибрали від марки 24 до марки 19, полігон ІV від М17 до М24. По намічених полігонах підраховують нев’язки в сумі перевищень. Напрямок обходу полігонів вибирають як по так і проти годинникової стрілки, але він повинен бути однаковий для всіх полігонів. Нев’язки, довжини полігонів (в км) і граничні нев’язки виписують на рисунку мережі всередині кожного полігону.

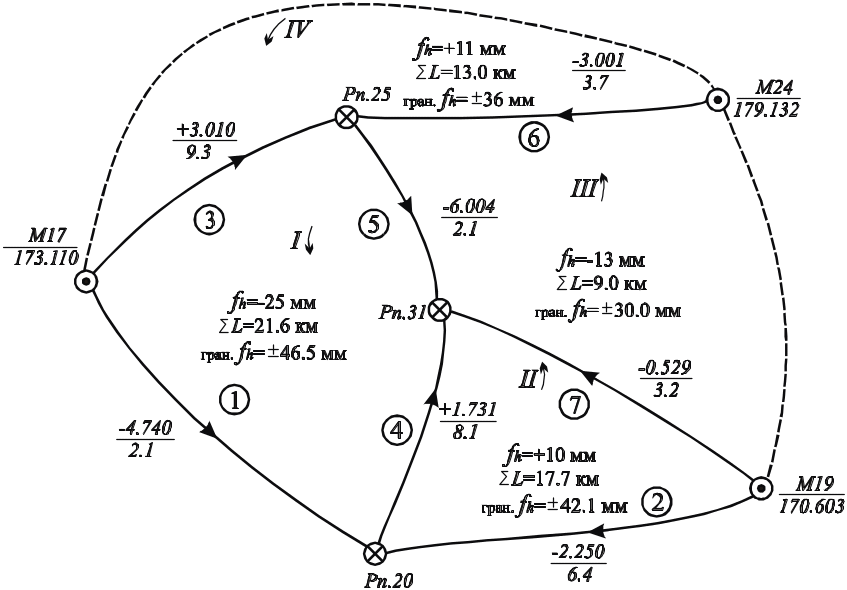
Рисунок 3.1 – Схема нівелірної мережі

Впевнившись, що нев’язки по всіх полігонах допустимі, переходять до вирівнювання мережі.

Для вирівнювання перевищень складають схему врівноваження методом В.В. Попова (рисунок 3.2). На цій схемі всередині кожного полігону під його номером викреслюють табличку нев’язок, а з зовнішнього боку полігону біля кожної ланки (ходу) – табличку поправок. Ходи, що належать двом суміжним полігонам, будуть мати дві таблички поправок. В таблички поправок записують відповідні значення нев’язок. В кожному полігоні нев’язку розподіляють прямопропорційно довжинам ходів (або оберненим вагам), застосовуючи формулу:

. (3.4)

Для скорочення обчислень в формулі (3.4) величини одержують для всіх ходів і записують червоним чорнилом над відповідними табличками поправок з зовнішнього боку полігону. Ці величини називають “червоними числами”, контролем обчислень яких є рівність одиниці їх суми по кожному полігону. Починати розподіл нев’язок можна з довільного полігону.

Почнемо з полігону I, що має найбільшу нев'язку по абсолютній величині і найбільше число спільних ходів з іншими полігонами. Нев'язку цього поліго­ну, що дорівнює +25, послідовно множать на червоні числа його ланок і одержані значення (заокруглюючи до цілих мілі­метрів) записують в таблички поправок під відповідними чер­воними числами. Знаки в одержаних значеннях будуть такі, як знаки нев'язок.

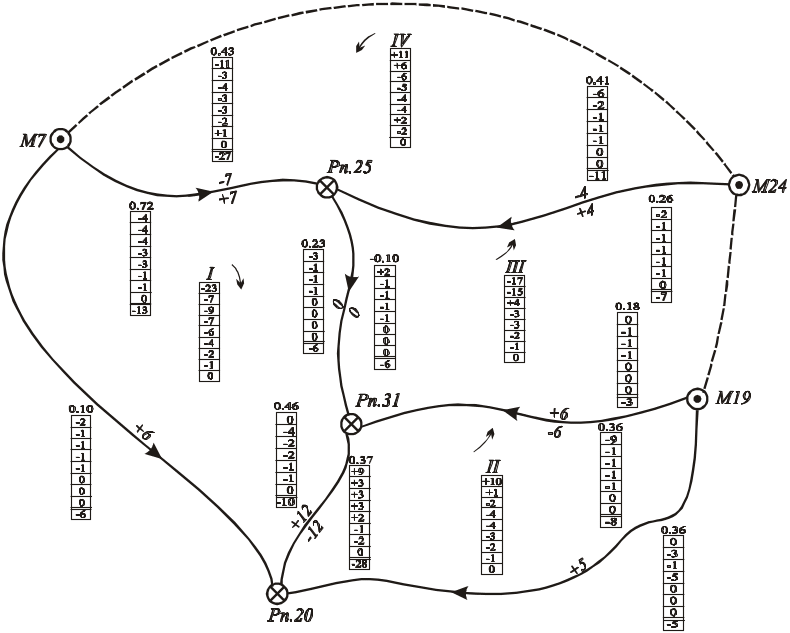
Рисунок 3.2 – Схема врівноваження методом В.В.Попова

Після цього переходять в наступний полігон, в нашому випадну в полігон ІІ. Нев'язка його стала рівна алгебраїчній сумі початкової нев'язки і поправки, одержаної на хід 4 із розподілу нев'язки в полігоні І, тобто нова нев'язка ви­явилась рівною –10 + 9 = - 1. Розподіляють цю пов'язку відповідно до червоних чисел 0.36; 0.46; 0.18 і одержують значення 0, 0, 0.

Потім підраховують нові нев'язки для полігонів Ш і ІV і розподіляють їх пропорційно червоним числам. Після закін­чення першого кола, переходять знову до початкового поліго­ну. Тепер його нев'язка буде складатись із поправок, одер­жаних по окремих ланках при розподілі нев'язок в суміжних полігонах. Її розподіляють з допомогою червоних чисел полігону І, одержані поправки записують у відповідні таблички. Потім переходять до наступних полігонів, проводячи аналогічні дії до тих пір, поки нев'язки всіх полігонів будуть дорівнювати нулю.

Далі підраховують алгебраїчну суму поправок по кожній табличці і підписують її під подвійною рискою. Поправ­ки в сумах перевищень по кожному ходу обчислюють за таким правилом: поправка в сумі перевищень ходу, що належить двом суміжним полігонам, одержується як алгебраїчна сума чисел внутрішньої і зовнішньої табличок, причому сума поправок зовнішньої таблички береться з оберненим знаком. Поправка в сумі перевищень ходу, що належить лише одному полігону, дорівнює сумі чисел зовнішньої таблички з оберненим знаком.

Далі за виправленими перевищеннями обчислюють висоти вузлових реперів (таблиця 3.1). При цьому поправки в перевищення виписують за прави­лом: якщо напрямок ходу при обчисленні висот співпадає з напрямком полігону, в який входить хід, поправка виписуєть­ся з тим знаком, з яким одержана з урівнювання, якщо напря­мок ходу при обчисленні відмітки не співпадає з напрямком полігону, в який входить хід, поправка виписується з оберненим знаком.

Таблиця 3.1- Відомість обчислень вирівняних значень перевищень і висот вузлових реперів

№ реперів	№ ходу	№ вихідних точок	Висоти вихідних точок	Переви-щення hi, м	Поправки νі, мм	Виправле-ні переви-щення hi, м	Висоти Ні, м	Довжина ходів Li, км
25	3 6	М17 М24	173.110 179.132	+3.010 -3.001	+7 -4	+3.017 -3.005	176.127 176.127	9.3 3.7	0.64 1.62	31.4 25.9
20	1 2	М17 М19	173.110 170.603	-4.740 -2.250	-6 +5	-4.746 -2.245	168.364 168.358	2.1 6.4	2.86 0.94	101.5 23.5
31	7 5 4	М19 Рп25 Рп20	170.603 176.127 168.361	-0.529 -6.044 +1.731	+6 0 -12	-0.523 -6.044 +1.719	170.080 170.083 170.080	3.2 2.1 8.1	1.87 2.86 0.74	67.3 0 106.6
										356.2