1.4 Аналіз результатів роботи, висновки

В результаті виконання даної роботи виконано вирівнювання полігонометричного ходу корелатним методом. Проведено оцінку точності результатів урівнювання.

2 Лабораторна робота № 2 урівнювання мережі тріангуляції параметричним методом

2.1 Мета, завдання і тривалість роботи

Вирівняти мережу тріангуляції параметричним методом. Тривалість роботи – 10 год.

2.2 Основні теоретичні положення

При вирівнюванні тріангуляції параметричним методом невідомі поправки в кути виражають у вигляді функцій, аргументами яких є поправки в координати невідомих пунктів і вільні члени. В загальному вигляді поправку кожного виміряного кута “i” між напрямками k і j (рисунок 2.1) можна записати так:

(2.1)

де , , , , , - поправки в координати пунктів “і”, “j”, “к”, виражені в дециметрах;

- вільний член.

Вирівнювання мережі можна виконати як по напрямках, так і по кутах.

Рисунок 2.1 – Схема кута

Розглянемо методику вирівнювання тріангуляційної мережі по кутах, яка дозволяє значно скоротити об’єми обчислювальних робіт.

При складанні параметричних рівнянь поправок можливі чотири наступні випадки:

а) всі пункти (i, k, j) невідомі:

(2.2)

б) відомі координати пункту і:

(2.3)

в) відомі координати пункту k:

(2.4)

г) відомі координати пункту j:

(2.5)

Коефіцієнти , , обчислюють за формулами:

, (2.6)

, (2.7)

де - приблизний дирекційний кут напрямку ik;

- довжина сторони, в км.

Вільний член рівнянь поправок обчислюють за формулою:

, (2.8)

де - виміряне значення кута на пункті і.

Для визначення числових значень коефіцієнтів і вільних членів параметричних рівнянь поправок вираховують приблизні значення сторін по виміряних кутах, а також координати невідомих пунктів і дирекційні кути всіх напрямків мережі.

Потім переходять безпосередньо до урівнювання, яке виконують в такій послідовності:

- складають рівняння поправок (з врахуванням обчислених раніше коефіцієнтів і вільних членів) для всіх виміряних кутів мережі;

- від лінійних рівнянь поправок переходять до нормальних, які розв’язують відомими методами;

- обчислюють остаточні значення координат пунктів мережі шля­хом введення в їх приблизні значення поправок, отриманих із розв’язання нормальних рівнянь;

- обчислюють поправки у виміряні кути і остаточно розв’язують трикутники;

- знову знаходять точні значення координат невідомих пунктів, використовуючи вирівняні значення сторін і кутів;

- виконують оцінку точності результатів вирівнювання.

Оскільки результати вимірів є рівноточними, середня квадратична помилка урівняного кута буде:

(2.9)

де V- поправки в кути, обчислені за результатами урівнювання;

r - число надлишкових вимірів, обчислене за формулі:

, (2.10)

де Д - число всіх виміряних кутів;

r - число невідомих пунктів;

t - число вихідних (твердих) пунктів.

На практиці переважно роблять оцінку точності найбільш слабого пункту мережі. Щоб визначити ваги P_XK, P_YK координат слабого пункту К, невідомі поправки , координат цього пункту ставлять відповідно на передостаннє і останнє місце в системі нормальних рівнянь. Із розв’язку системи нормальних рівнянь в схемі Гауса вага P_YK останнього невідомого дорівнює квадратичному коефіцієнту С при в останньому перетвореному нормальному рівнянні. Вагу P_XK передостаннього невідомого знаходять за формулою:

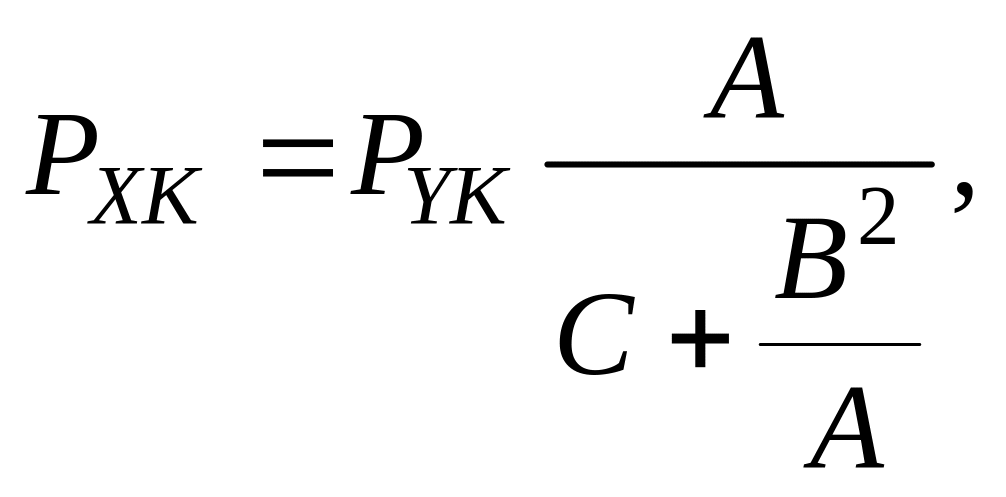(2.11)

де А - квадратичний коефіцієнт передостаннього перетвореного нормального рівняння;

В - коефіцієнт при в передостанньому перетвореному рівнянні.

Середні квадратичні похибки абсцис і ординат пункту вираховують за формулами:

(2.12)

Похибка положення пункту дорівнює:

. (2.13)