
О Н М А
Кафедра вищої математики
Програма восьмого модульного контролю
Елементи теорії стійкості. Теорія ймовірності і математична статистика.
2 курс 2 семестр ФМС
Склав проф. Попов В. Г.
Затверджено на засіданні кафедри протокол № _ __
від 2007р.
Завідувач кафедри вищої математики проф. Попов В. Г.
Одеса 2007
Теоретичні запитання.
Визначення стійкості незбуреного розв’язка системи диференціальних рівнянь за Ляпуновим.(397-398)
Визначення асимптотичної стійкості незбуреного розв’язка системи диференціальних рівнянь за Ляпуновим.(397-398)
Нульовий розв’язок системи диференціальних рівнянь і його стійкість.(с.399)
Поняття збурень розв’язка системи диференціальних рівнянь. Визначення стійкості через збурення.(с.402-403)
Система диференціальних рівнянь для збурень і її властивості.(с.404-405).
Система диференціальних рівнянь для збурень у випадку лінійної системи.(с.413).
Теорема о стійкості розв’язків лінійної системи диференціальних рівнянь.(с.414).
Теорема про стійкість нульового розв’язку однорідної системи зі сталими коефіцієнтами.
Лінеаризація системи диференціальних рівнянь для збурень. Система першого наближення.(с.43-416)
Теорема Ляпунова про стійкість за першим наближенням.(с.418)
Визначення стійкості за Ляпуновим незбуреного розв’язка диференціального рівняння
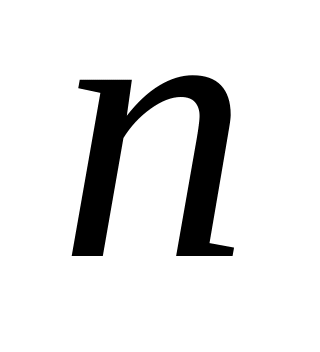 -го
порядку.(с.425)
-го
порядку.(с.425)Визначення асимптотичної стійкості незбуреного розв’язка диференціального рівняння -го порядку. (с.425)
Нульовий розв’язок диференціального рівняння і його стійкість.(с.425).
Поняття збурень розв’язка диференціального рівняння. Визначення стійкості через збурення.(с.425-426)
Диференціальне рівняння для збурень і його властивості.(с.426)
Теорема про стійкість розв’язка лінійного диференціального рівняння .(с.426)
Теорема про стійкість нульового розв’язка лінійного однорідного рівняння зі сталими коефіцієнтами. (с.426)
Необхідна умова від’ємності дійсних частин характеристичного рівняння.(с.429)
Матриця Раусса- Гурвиця. Критерій Раусса-Гурвиця.(с.429-430).
Матриця Раусса- Гурвиця. Критерій Льєнара-Шіпара.(с.431-432)
Критерій Михайлова.(с.433-435)
Поняття події. Класифікація випадкових подій.(с.504-507).
Теоретичне визначення ймовірності події. Загальні властивості ймовірності.
Статистичне визначення ймовірності. Властивість стійкості відносних частот. Загальні властивості ймовірності.(с. 504-507)
Додавання подій і його властивості.(с.501-502)
Множення подій і його властивості.(с.501-502)
Теорема про ймовірність суми несумісних подій і наслідки з неї.(с. 511)
Залежні і незалежні події. Умовні ймовірності.(с. 517)
Теорема про ймовірність добутку подій і наслідки з неї.(с.514)
Теорема про ймовірність суми двох довільних подій.(с.512-513)
Теорема появи хоча б однієї з незалежних подій.(с. 517-518)
Формула повної ймовірності.(с. 515)
Формула Байєсса (гіпотез).(с.510)
Послідовність незалежних випробувань. Формула Бернуллі.(с.519-521)
Послідовність незалежних випробувань. Формула Пуассона.(с. 519-520,с. 521-522).
Послідовність незалежних випробувань. Локальна теорема і формула Муавра- Лапласа. Властивості функції ймовірності.(с. 519-520,523-524)
Послідовність незалежних випробувань. Інтегральна теорема і формула Муавра- Лапласа. Властивості інтеграла ймовірності.(с.519-520,526-528)
Поняття випадкової величини. Дискретні і неперервні , одновимірні і багатовимірні випадкові величини(529-532).
Поняття закону розподілу. Ряд і многокутник розподілу дискретної випадкової величини.(529-532)
Поняття закону розподілу. Функція розподілу. Функція розподілу одновимірної дискретної випадкової величини.(530,537).
Поняття закону розподілу. Функція розподілу одновимірної і двовимірної випадкової величини.(532-533).
Поняття закону розподілу. Густина розподілу одновимірної і двовимірної випадкової величини.(539-540)
Функція розподілу одновимірної випадкової величини і її властивості.(532-538)
Функція розподілу двовимірної випадкової величини і її властивості.(532-538)
Густина розподілу одновимірної випадкової величини і її властивості.(539-542)
Функція розподілу двовимірної випадкової величини і її властивості.(539-542)
Математичне сподівання дискретної випадкової величини . Властивості математичного сподівання. (545-546,553-558).
Математичне сподівання неперервної випадкової величини. Властивості математичного сподівання.(545-546,553-558).
Дисперсія і середнє квадратичне відхилення. Властивості дисперсії.(555-558)
Початкові і центральні моменти вищих порядків.(569)
Кореляційний момент . Коефіцієнт кореляції.(561-562)
Незалежні і залежні випадкові величини. Умова незалежності.(561-562)
Рівномірний закон розподілу. (565-566).
Експоненціальний закон розподілу.(574-575)
Одновимірній нормальний закон розподілу.(567-568)
Двовимірний нормальний закон розподілу.(571-572)
Побудова еліпса розсіювання.(571-572)
Вибірка і простий варіаційний ряд. Інтервальний ряд. Статистична функція розподілу.(606-607)
Вибірка і простий варіаційний ряд. Інтервальний ряд. Гістограма і статистична густина розподілу.(606-607)
Вибіркові оцінки математичного сподівання і дисперсії (вибіркове середнє і вибіркова дисперсія). (с. 611-615).
Незміщеність вибіркової оцінки математичного сподівання.(с. 611-615)
Незміщенність вибіркової оцінки дисперсії.(с. 611-615)
Нерівність Чебишева.(с.555)
Спроможність вибіркових оцінок. Ефективність вибіркових оцінок.(611-615)
Довірчий інтервал і надійність.(с. 616-617)
Довірчий інтервал для дисперсії при нормальному розподілі.(с. 617)
Довірчий інтервал для математичного сподівання при нормальному розподілі.(с.617-619)
Метод найбільшої правдоподібності.(с.609-610)
Визначення параметрів нормального розподілу методом найбільшої правдоподібності.(с.610-611)
Статистичні гіпотези та їх перевірка. Критерії згоди.(620-621)
Критерій згоди
 Пирсона.(с.623-625).
Пирсона.(с.623-625).Критерій згоди Колмогорова.(с.621-622).
Теорема Чебишева.(с.580-582).
Закон великих чисел.(с. 581-582).
Теорема Бернуллі.(с.582-583).
Центральна гранична теорема Ляпунова.(с. 587).
Практичні завдання.
Дослідити на стійкість за першим наближенням :
 .
.Дослідити на стійкість за першим наближенням.:

Дослідити на стійкість за першим наближенням
 .
.Дослідити на стійкість за першим наближенням:

Дослідити на стійкість за першим наближенням:
 .
.Дослідити на стійкість за першим наближенням:
 .
.Дослідити на стійкість за першим наближенням:
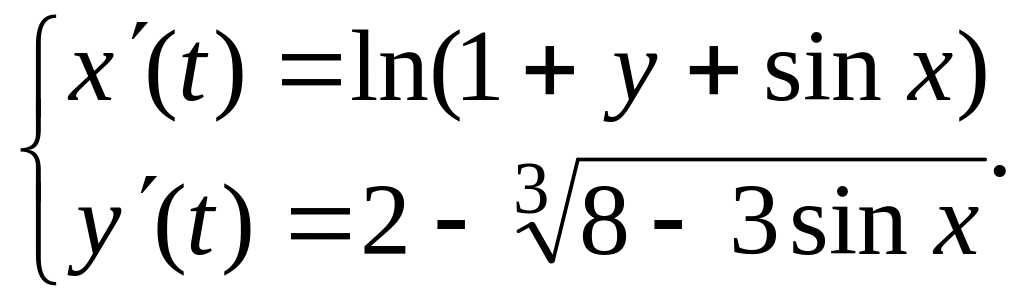
Дослідити на стійкість за першим наближенням:
 .
.Дослідити на стійкість за першим наближенням:
 .
.Дослідити на стійкість за першим наближенням:

Дослідити на стійкість за першим наближенням:
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Раусса-Гурвіца :

Дослідити на стійкість нульовий розв’язок за допомогою критерію Михайлова :

Дослідити на стійкість нульовий розв’язок за допомогою критерію Михайлова :
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Льєнара -Шіпара: .
При яких значеннях
 буде стійким нульовий розв’язок
рівняння
буде стійким нульовий розв’язок
рівняння

Дослідити на стійкість нульовий розв’язок за допомогою критерію Михайлова:
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Льєнара -Шіпара:

При яких значеннях
 буде стійким нульовий розв’язок
рівняння
буде стійким нульовий розв’язок
рівняння

Дослідити на стійкість нульовий розв’язок за допомогою критерію Раусса-Гурвіца:

Дослідити на стійкість нульовий розв’язок за допомогою критерію Раусса-Гурвіца:

Дослідити на стійкість нульовий розв’язок за допомогою критерію Льєнара_Шіпара :
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Михайлова:
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Михайлова:
Дослідити на стійкість нульовий розв’язок за допомогою критерію Михайлова
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Раусса-Гурвіца:
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Михайлова:
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Раусса-Гурвіца:
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Михайлова:
 .
.Дослідити на стійкість нульовий розв’язок за допомогою критерію Раусса-Гурвіца: .
Ймовірність браку при виданні одного примірника книги
 0,0001. Знайти ймовірність того що тираж
в 50000 примірників містить не більш як
4 бракованих книги.
0,0001. Знайти ймовірність того що тираж
в 50000 примірників містить не більш як
4 бракованих книги.
Виготовлено 625 деталей. Ймовірність того що при виготовленні буде отримана якісна деталь p=0.64. Знайти ймовірність того, що сере виготовлених деталей рівно 370 якісних. Не менш як 370 якісних,
В першій урні 8 білих і 10 чорних куль, в другий 6 білих і 4 чорних. З першої урни в другу переклали дві кулі, а потім з другої урни взяли кулю. Знайти ймовірність того ,що ця куля чорна.
Ймовірність влучання в ціль при одному пострілі для кожної з двох гармат відповідно дорівнює
 і
і .
Знайти ймовірність того що при залпі
влучить :1) тільки одна гармата; 2) хоча
б одна гармата.
.
Знайти ймовірність того що при залпі
влучить :1) тільки одна гармата; 2) хоча
б одна гармата.Виготовлено 400 деталей. Ймовірність того що при виготовленні буде отримана якісна деталь p=0.8. Знайти ймовірність того, що сере виготовлених деталей рівно 300 якісних. Не менш як 300 якісних,
Пристрій складається з 1000 елементів які працюють незалежно. Ймовірність відмови кожного з них
 .Знайти
ймовірність того , що відмовить не
більш 4 елементів.
.Знайти
ймовірність того , що відмовить не
більш 4 елементів.Монету кидають 8 разів. Знайти ймовірність того що герб з’явиться не менше 5 разів.
Ймовірність виготовлення неякісної деталі
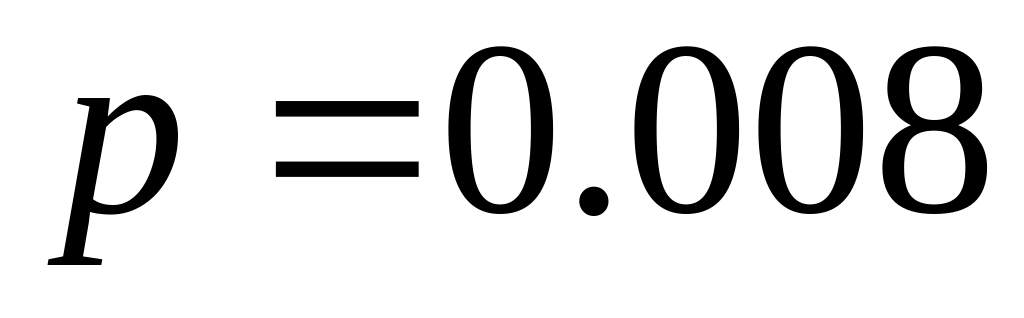 .
Знайти ймовірність того що з 500 деталей
не більше 4 неякісних.
.
Знайти ймовірність того що з 500 деталей
не більше 4 неякісних.Пристрій складається з двох елементів які працюють незалежно. Ймовірність відмови кожного з них дорівнює 0.05. Обчислити імовірності відмови: а) хоча б одного єлемента;б) тільки одного елемента; в) безвідмовної роботи.
В першій урні 5 білих і 10 чорних куль, в другий 4 білих і 6 чорних. З першої урни в другу переклали дві кулі, а потім з другої урни взяли кулю. Знайти ймовірність того ,що ця куля біла.
Ймовірність того що в ціль влучать при одному пострілі для першого стрільця дорівнює 0.8, а для другого 0.6. Першій зробив три постріли , а другий два постріли. Знайти ймовірність хоча б одного влучення у ціль.
Виготовлено 300 деталей. Ймовірність того що при виготовленні буде отримана якісна деталь p=0.75. Знайти ймовірність того, що серед виготовлених деталей рівно 240 якісних. Не менш як 240 якісних.
Виготовлено 4000 деталей. Ймовірність того що при виготовленні буде отримана якісна деталь p=0.9. Знайти ймовірність того, що серед виготовлених деталей неменше як 90% якісних. Рівно 90% якісних.
В двох партіях відповідно 96% і 80% якісних деталей. Вибирається по одній деталі з кожної партії. Знайти ймовірність того що серед них : 6) тільки одна неякісна; хоча б одна неякісна.
Ймовірність влучання в ціль при одному пострілі дорівнює 0.8.Знайти ймовірність того що при 100 пострілах буде не менше як 75 влучань.
Виготовлено 400 деталей. Ймовірність того що при виготовленні буде отримана якісна деталь p=0.75. Знайти ймовірність того, що серед виготовлених деталей рівно 300 якісних. Не менш як 300 якісних.
В двох партіях відповідно 76% і 60% якісних деталей. Вибирається по одній деталі з кожної партії. Знайти ймовірність того що серед них : 6) тільки одна неякісна; хоча б одна неякісна.
Ймовірність влучання в ціль при одному пострілі дорівнює 0.6.Знайти ймовірність того що а)при 100 пострілах буде не менше як 50 влучань;б) при 100 пострілах буде рівно 50 влучань.
В першій урні 5 білих і 10 чорних куль, в другий 6 білих і 4 чорних. З першої урни в другу переклали дві кулі, а потім з другої урни взяли кулю. Знайти ймовірність того ,що ця куля біла.
В урні 15 куль з яких 5 білих і десять чорних. Послідовно без повернення беруть дві кулі. Знайти ймовірності: а) обидві білі; б) обидві чорні ; в) кулі різного кольору.
В першій урні 10 білих і 5 чорних куль, в другий 8білих і 4 чорних. З першої урни в другу переклали дві кулі, а потім з другої урни взяли кулю. Знайти ймовірність того ,що ця куля біла.
Ймовірність браку при виданні одного примірника книги 0,0002. Знайти ймовірність того що тираж в 30000 примірників містить не більш як 3 бракованих книги.
Виготовлено 400 деталей. Ймовірність того що при виготовленні буде отримана якісна деталь p=0.64. Знайти ймовірність того, що сере виготовлених деталей рівно 300 якісних. Не менш як 300 якісних,
В першій урні 6 білих і 14 чорних куль, в другий 6 білих і 4 чорних. З першої урни в другу переклали дві кулі, а потім з другої урни взяли кулю. Знайти ймовірність того ,що ця куля біла.
Ймовірність влучання в ціль при одному пострілі для кожної з двох гармат відповідно дорівнює
 і
і .
Знайти ймовірність того що при залпі
влучить :1) тільки одна гармата; 2) хоча
б одна гармата.
.
Знайти ймовірність того що при залпі
влучить :1) тільки одна гармата; 2) хоча
б одна гармата.Пристрій складається з 10000 елементів які працюють незалежно. Ймовірність відмови кожного з них
 .Знайти
ймовірність того , що відмовить не
більш 3 елементів.
.Знайти
ймовірність того , що відмовить не
більш 3 елементів.Пристрій складається з двох елементів які працюють незалежно. Ймовірність відмови кожного з них дорівнює 0.06. Обчислити імовірності відмови: а) хоча б одного елемента;б) тільки одного елемента; в) безвідмовної роботи.
В першій урні 10 білих і 5 чорних куль, в другий 6 білих і 4 чорних. З першої урни в другу переклали дві кулі, а потім з другої урни взяли кулю. Знайти ймовірність того ,що ця куля чорна.
Виготовлено 2500 деталей. Ймовірність того що при виготовленні буде отримана якісна деталь p=0.9. Знайти ймовірність того, що серед виготовлених деталей : а)рівно як 90% якісних., б)не менше як 90% якісних.
В двох партіях відповідно 90% і 80% якісних деталей. Вибирається по одній деталі з кожної партії. Знайти ймовірність того що серед них : 6) тільки одна неякісна; а)хоча б одна неякісна.
Випадкова величина

 розподілена за показниковим законом
і
розподілена за показниковим законом
і
 .
Знайти густину розподілу і ймовірність
.
Знайти густину розподілу і ймовірність
 .
.Є закон розподілу випадкової величини
X |
3 |
4 |
5 |
6 |
P |
0.3 |
0.2 |
? |
0.1 |
Знайти
![]() і побудувати графік функції розподілу.
і побудувати графік функції розподілу.
