10

Лекція №5.

1. Визначення втрат напору при русі рідини у трубопроводах

2.Визначення втрат на місцеві опори

3. Визначення діаметра трубопроводу

1. Визначення втрат напору при русі рідини у трубопроводах

Згідно рівняння Бернуллі для реальної рідини напір в трубопроводі в напрямку руху рідини зменшується на величину втрат

(1)

де h_вт-втрати напору при русі рідини

Загальні втрати напору h_вт складаються з втрат на тертя та втрат на місцеві опори

(2)

- загальні втрати напору в [м]; - втрати на тертя (за рахунок тертя до стінки труби і шарів рідини між собою); - втрати на місцеві опори (вони виникають у випадку, коли рідина змінює напрямок або швидкість руху)

1. Визначення втрат на тертя.

Розглянемо горизонтальний трубопровід (z₁=z₂); нехай відповідно

Запишемо Рівняння Бернуллі для реальної рідини

де h_вт=h_т

тоді

а) випадок для ламінарного руху

Рівняння Пуазейля

де витрата (3)

(4)

З рівнянь (3) і (4) після перетворень одержуємо

(5)

або

(6)

- формула Дарсі (6) визначає втрати напору на тертя при ламінарному режимі руху

[м] (7)

- коефіцієнт тертя; для круглої труби (64- коефіцієнт, коли труби круглого січення)

для довільного перерізу (В – коефіцієнт, що визначається з довідника)

б) випадок для турбулентного руху (Re>10000)

Для турбулентного потоку для визначення h_т. використовують також рівняння (7). Однак, вираз для коефіцієнта тертя не може бути виведений теоретично через складність структури турбулентного потоку

(8)

Виділяють два випадки в залежності від шорсткості труб (середньої висоти виступів Δ або відносної шорсткості е)

1. гідравлічно гладкі труби (шорсткість незначна ). В даному випадку

(9)

2. гідравлічно шорсткі труби ( ). В цьому випадку

- формула Нікурадзе (10)

Режим, коли не залежить від , називається автомодельним

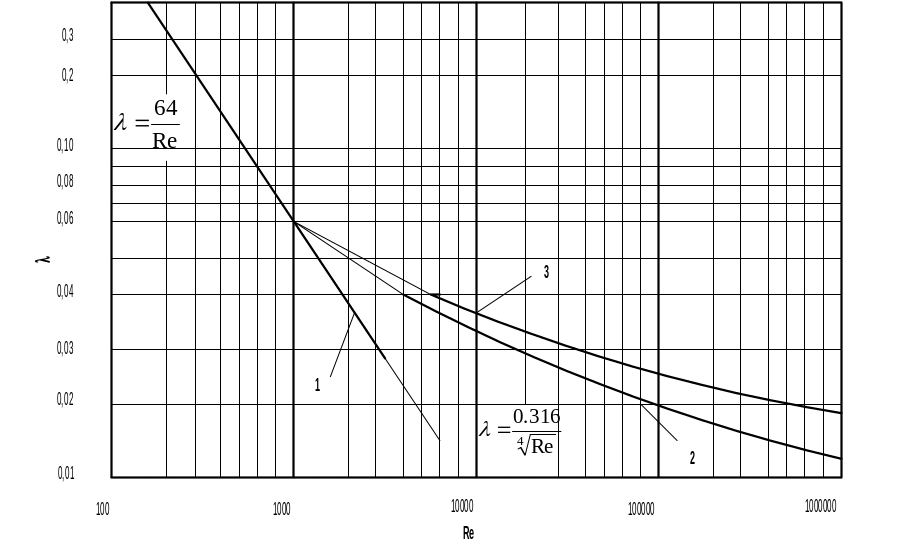
Рис. Залежність λ від Re:

1 – гладкі і шорсткі труби; 2- гладкі труби; 3- шорсткі труби.

Таким чином, шорсткість при ламінарному режимі не впливає на λ через значну величину гідравлічного пограничного шару рідини біля стінки, в якому “ховаються” виступи стінки.

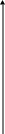
δ

турбулентний чи ламінарний потік.

в ламінарному підшарі домінують сили “в’язкості”.

Вплив шорсткості при турбулентному режимі на величину λ визначається співвідношенням між середньою висотою виступів Δ і товщиною в’язкого підшару δ, рух рідини в якому можна вважати практично ламінарним.

Товщина в’язкого підшару визначається як де

і визначається в залежності від числа Re Якщо число дуже велике, можливі два випадки

1. - формула Нікурадзе

2. - автомодельна область

а це відповідно задає область тертя