Результаты статистических исследований ортогональных преобразований

Степень сжатия	Среднеквадратичные (максимальные) ошибки преобразований
	Хаара	Уолша - Адамара	Синусное	Косинус­ное
4.0	2.38(7)	2.42(7)	2.04(5)	1.61(4)
4.5	2.56(7)	2.82(8)	2.22(7)	1.61(5)
5.0	2.72(7)	2.77(9)	2.34(6)	1.61(6)

Как следует из этой таблицы, косинусное преобразование имеет несомненные преимущества перед преобразованиями Хаара, Уолша-Адамара и синусным.

Возможно построение других видов унитарных преобразований. Так, например, известно ортогональное наклонное или слэнт-преобразование, кото­рое обладает базисными функциями, имеющими вид кусочно-линейных функций. При N=2 наклонное преобразование совпадает с преобразованием Адамара второго порядка. Это преобразование при обработке изображений имеет несколько меньшую эффективность, чем дискретное косинусное преобразование. Унитарное преобразование может быть построено также на основе использования полиномов Лежандра. Применение этого преобразования для обработки изображений показало такую же эффективность, как и при использовании дискретного косинусного преобразования. Однако быстрый алгоритм вычисления этого преобразования пока не найден.

Рассмотрев наиболее распространенные унитарные преобразования, применяемые в цифровой обработке сигналов, следует сделать некоторые замечания, связанные с двумерностью преобразований.

При разбиении изображения на прямоугольные блоки и применении, скажем, к стро­кам этих блоков линейных преобразований, компоненты образов оказываются коррелированными по вертикали, что позволяет применить к столбцам из этих компонент свое преобразование. Оно, вообще говоря, необязательно должно быть тем же, что и для обработки горизонтальных отрезков исходного изображения.

В ряде исследований использовался метод гибридного преобразования, при кото­ром сначала производилось одномерное косинусном преобразование отрезков строк, а затем над полученными коэффициентами осуществлялась вертикальная ДИКМ. Любо­пытно, что при достаточно глубоком квантовании (объём передаваемой информации менее 0,5 бит/пиксель) результат получился лучше, чем при применении двумерного косинусного преобразования.

Однако с учетом того, что в большинстве случаев алгоритмы вычислений для NxN двумерных преобразований работают быстрее, чем для линейных порядка N², практи­ческое применение находят именно двумерные преобразования.

Квантование коэффициентов преобразования

Сами по себе унитарные дискретные преобразования определены над функциями, имеющими дискретную область определения, но непрерывную область значений, т.е. значения, характеризующие уровни пикселей и величины компонент преобразования, могут быть и не целочисленными.

В то же самое время на вход кодера нужно подавать одномерную последователь­ность дискретных символов. Она получается при квантовании величин компонент пре­образования и расстановке их в линейный ряд.

В самом общем случае процесс квантования – это осуществление нелинейного преобразования, характеристика которого имеет вид монотонной ступенчатой функции. Распределение величин шагов квантования можно оптимизировать, например, по среднеквадратичной ошибке для заданного распределения плотности вероятностей сходной функции и количества дискретных уровней (процедура Ллойда-Макса).

Исследования показывают, что компоненты унитарных преобразований изображений имеют распределение, подчиняющееся либо нормальному, либо лапласовому зако­нам. Для этих случаев при большом числе уровней преобразования близким к опти­мальному является квантование с равномерной шкалой в соответствии с формулой:

F_q=round (F/k), где F и F_q – соответственно квантуемая и квантованная величи­ны, k – коэффициент преобразования.

При восстановлении изображения компоненты унитарных преобразований умножа­ются на коэффициент k. Следует отметить, что при этом минимизируется средне­квадратичное отклонение восстановленного (после обратного ортогонального преоб­разования Т) изображения от исходного, поскольку

Последняя строка вытекает из равенства Парсеваля. Заметим, что минимизация среднеквадратичного отклонения значений пикселей при восстановлении изображе­ний, строго говоря, не обеспечивает минимизации максимальной ошибки в преобра­зуемом блоке

max{abs[X_вых (i, j) – Х_вх (i, j)]} => min

Эта задача может быть решена лишь методами целочисленного программирования. Возможен другой подход к выбору алгоритма квантования коэффициентов унитар­ных преобразований, связанный с учетом субъективной чувствительности глаза к раз­личным пространственным частотам, учитывая, что при передаче более высокочас­тотных компонент допустима большая погрешность.

При этом результаты унитарного преобразования подвергаются квантованию в соответствии с формулой

F_q(u,v)=round{F(u,v)/[kQ(u,v)]}, u, v = 0,...,N-1.

Для различных массивов данных, например, для сигналов яркости и цветоразностных сигналов, могут применятся различные таблицы коэффициентов преобразования. Такие таблицы могут передаваться вместе с кодируемыми изображениями.

Применение общего множителя k позволяет линейно изменять таблицу квантования. Выбор и применение конкретных таблиц могут быть осуществлены по усмотрению пользователей, т.к. они могут быть оптимизированы для конкретных приложений.

Кодирование коэффициентов преобразования

После квантования компоненты унитарных преобразований, в частности ДКП, блоков изображения группируются в определенной последовательности, а затем кодируются хаффмановским или арифметическим кодером.

Метод группировки коэффициентов преобразования имеет большое значение для уменьшения объема передаваемой информации. Одним из вариантов группировки коэффициентов ДКП является Z-упорядочивание в соответствии со схемой рис. 9.10.а.

В этом случае коэффициенты выстраиваются в последовательности возрастания пространственных частот, причем, если пространственные частоты одинаковы, то предпочтение отдается коэффициентам с меньшими вертикальными частотами. Возможны и другие варианты группирования коэффициентов:

- если в блоке изображения в основном имеется горизонтальная структура измене­ния значений пикселей, то более эффективно вертикальное упорядочивание рис. 9.10.б;

• при вертикальной структуре изменения значений пикселей более удобно горизонтальное упорядочивание рис. 9.10. в;

• иногда используется структура рис. 9.10. г, подобная Z – упорядочиванию, но с предпочтением к коэффициентам с меньшими горизонталь­ными частотами. Часто для повышения эффективности кодирования коэффициен­ты F_kl(0,0) разных блоков (k, I - соответственно номера блоков по горизонтали и вертикали) изображения, характеризующие средние их яркости, группируют и пе­редают отдельно, предварительно осуществляя их обработку с использованием алгоритмов предсказания.

ВАРИАНТЫ ЛИНЕЙНОГО УПОРЯДОЧИВАНИЯ

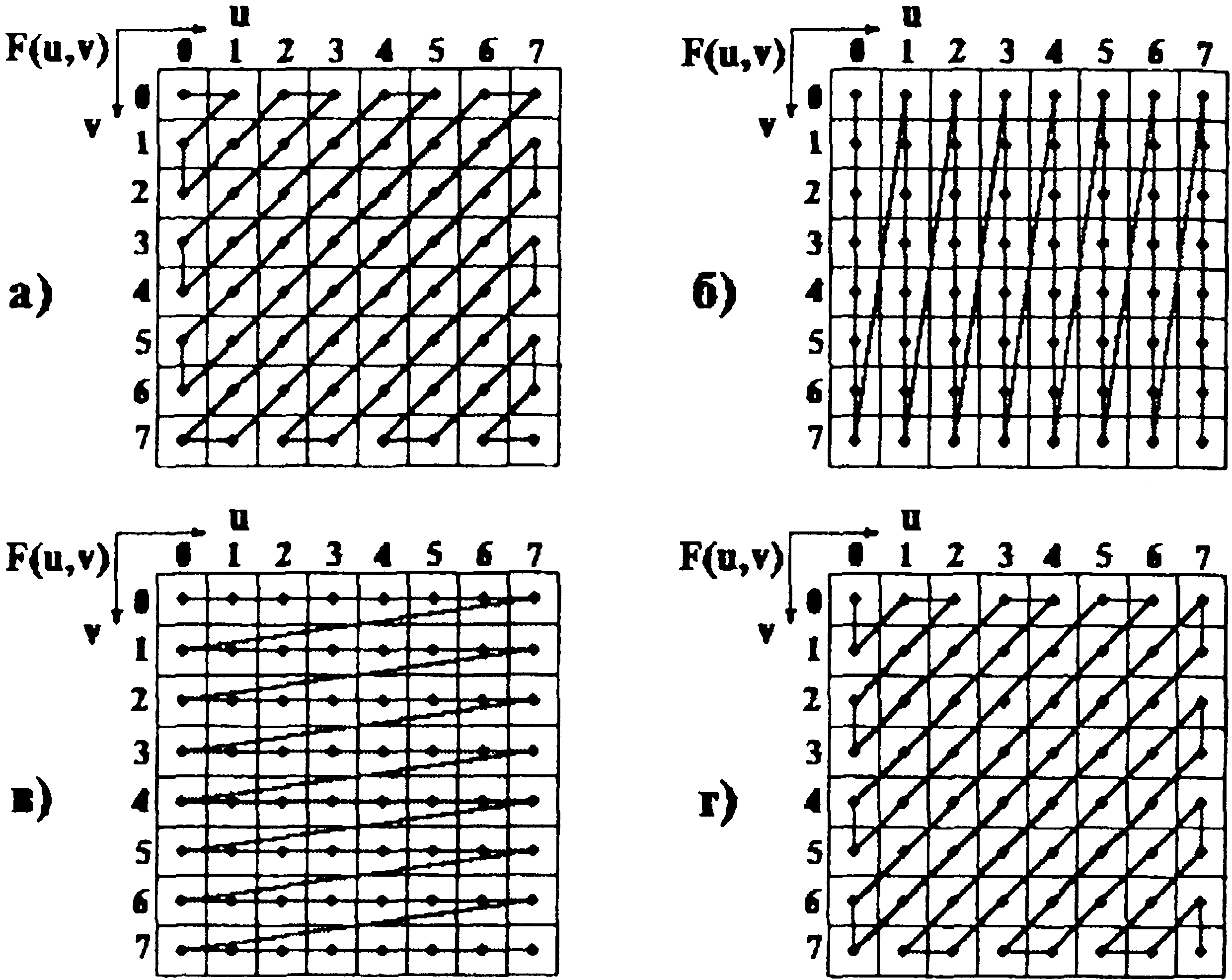
Рис. 9.10. Варианты упорядочивания коэффициентов дискретного косинусного преоб­разования

Другие методы интерполяционного и блочного кодирования

Одним из методов блочного кодирования является векторное кодирование, при котором весь набор блоков (векторов) изображения приводится к некоторому конечному набору.

При этом вместо непосредственной передачи кодовых последовательностей, характеризующих значения пикселей в каждом блоке, передается лишь номер блока.

Количество возможных векторов (блоков изображения) определяется при этом пропускной способностью канала.

Основным преимуществом векторного квантования является простая структура приёмника, который имеет лишь кодовую таблицу векторов, а воспроизведение изображения осуществляется путем последовательной расстановки этих векторов по поступающей из канала связи информации.

При адаптивном векторном квантовании, кроме того, передается также информация об эталонных векторах.

Существенными недостатками векторного кодирования является, с одной стороны, сложность кодера, а, с другой – плохая аппроксимация изображений, отличающихся от тех эталонных, по которым составлялась кодовая таблица.

Следует отметить, что существуют специальные алгоритмы формирования кодовых таблиц с использованием эталонных изображений. Иногда для ускорения процесса векторного кодирования и увеличения скорости передачи блоки изображения разби­ваются на классы, для каждого из которых составляется своя кодовая таблица.

Алгоритмы векторного кодирования обеспечивают формирование специального на­бора блоков изображения (кодовой книги), составленного по принципу наилучшего приближения к блокам исходного изображения (например, минимизацией среднеквад­ратичного отклонения).

Содержание кодовой книги и номера (кодовые слова) ее элементов, на которые бы­ли заменены блоки исходного изображения, упорядоченные в порядке сканирования этих блоков (например, слева направо; сверху вниз), передаются декодеру; при этом количество элементов этой книги должно быть меньше количества блоков исходного изображении.

Если рассматривать различные блоки размера nm пикселей как точки-вектора в nm – мерном пространстве изображений, то процесс замены их на элементы кодовой книги выглядит как квантование (вообще говоря, неравномерное) такого пространства на области сложной формы, окружающие точки соответствующие изображениям – элементам кодовой книги (от чего и происходит название метода). Пусть исходное изображение имеет размерность NM пикселей.

При прямоугольном разбиении получается блоков размерности nm. Если кодовая книга будет содержать k элементов, то на ее передачу потребуется knml бит, а последовательность кодовых слов займет еще бит, где l - разрядность оцифровки пикселей исходного изображения, в подавляющем большинстве случаев равная 8. При этом достигается степень сжатия равная

где - степень сжатия кодовой книги, которая может быть упакована с помощью ка­ких-либо методов компрессии без потерь информации, причем реально достижимое составляет около 2.

Очевидно, что сжатие с помощью векторного квантования предполагает обязательную потерю части информации, т.е. внесение искажений в исходное изображение. В про­цессе оптимизации процесса векторного квантования эти искажения минимизируются (при заданной степени сжатия, или, наоборот, достигается максимальное сжатие при заданном уровне допустимых искажений) путем:

а) выбора оптимального размера блока nm;

б) выбора оптимального размера кодовой книги k;

в) составления оптимального набора изображений - элементов кодовой книги.

Вообще говоря, существует и может быть найден глобальный оптимум одновре­менно по всем 3-м перечисленным параметрам. Положение этого оптимума опреде­ляется распределением NM/nm точек-блоков из исходного изображения в n-m-мерных пространствах изображении при различных nm. При равномерном распределении, что соответствует некоррелированному шуму в исходном изображении, оптимальным оказывается равномерное квантование каждого пикселя исходного изображения, т.е.

где d - максимальная ошибка квантования; - количество дискретных уровней в исходном изображении, K_i - i-ый уровень вос­производимых дискретных значений яркости пикселей. В изображении с коррелированными значениями яркости пикселей, точки-блоки рас­пределены в пространстве изображений неравномерно и центром "сгустков" таких то­чек, т.е. точек, в которых плотность вероятности нахождения блока из исходного изо­бражения имеет локальный максимум, могут составить набор элементов кодовой кни­ги, так что усредненная по исходному изображению ошибка, вносимая векторным квантованием, окажется меньшей, чем, например, при равномерном квантовании про­странства изображений.

Следует заметить, что использованная выше в целях изложения сути метода вектор­ного квантования модель представления блоков изображения в виде точек в много­мерном пространстве изображений с вычислительной точки зрения слишком сложна, т.к. при этом придется работать с массивами данных объемом в бит, что со­ставляет, например, для блоков 44 пикселя и I=8 2¹²⁸ - неприемлемую величину. В описываемых в литературе реальных исследовательских схемах, как правило, объем кодовой книги и размерность блоков выбирают, исходя из ожидаемой степени сжатия (для comp =10 обычно выбирают nm=16 (блоки 44); для comp=30 – nm=64 (блоки 88); количество элементов кодовой книги k обычно достигает нескольких тысяч). Ос­новными задачами оптимизации кодирования при этом оказываются:

а) составление оптимального набора изображений – элементов кодовой книги;

б) поиск элемента кодовой книги – наилучшим образом соответствующего очеред­ному кодируемому блоку из исходного изображения.

Алгоритм LBG

В 1980 году Linde, Buzo и Gray предложили алгоритм составления кодовой книги, дающий наилучшие до сего дня результаты. Этот алгоритм, именуемый LBG, состоит из двух процедур, последовательно-итерационно применяемых к системе – исходное изо­бражение плюс кодовая книга, полученная в результате применения какого-либо иного предварительного алгоритма, или составленная наугад из случайных изображений (от качества этой предварительной кодовой книги зависит лишь число итераций, которые необходимо будет произвести, прежде чем кодовая книга перестанет изменяться при каждой следующей итерации).

Алгоритм предусматривает реализацию последовательности итерационных процедур.

1. Процедура присваивания блокам исходного изображения соответствия тому или иному элементу текущей кодовой книги. При этом множество блоков, составляющих исходное изображение, разбивается на непересекающиеся подмножества, состоящие из блоков исходного изображения (необязательно в одном и том же количестве) близ­ких друг к другу и к некоторому элементу кодовой книги, в соответствии с некоторой мерой (например, среднеквадратичным или максимальным отклонением яркости по блоку). При этом число непересекающихся подмножеств должно быть равно количе­ству элементов текущей кодовой книги (оно может быть меньше конечной величины k).

2. Процедура "улучшения" текущей кодовой книги – замена ее элементов путем построения для каждого из полученных в предыдущей процедуре подмножеств блоков такого элемента кодовой книги, который бы минимизировал некоторое среднее откло­нение от него всех блоков подмножества в смысле выбранной меры. При этом блоков - новых элементов кодовой книги, соответствующих каждому подмножеству, может быть и больше одного. Тогда происходит "расщепление" элемента текущей кодовой книги, так что ее объем может быть постепенно доведен до заранее выбранного значения k.

Если "расщепления" не происходит, то новый блок - элемент кодовой книги нахо­дится, например, путем попиксельного арифметического усреднения яркостей всех блоков подмножеств при использовании в качестве меры среднеквадратичного откло­нения или же путем определения медианы значений яркостей соответствующих пикселей по всему подмножеству блоков при использовании в качестве меры максимального отклонения.

Обычно нахождение оптимальной кодовой книги осуществляется упрощен­ными способами – от случайного разбиения подмножеств на ряд более мелких, до вы­бора в качестве новых элементов кодовой книги векторов собственной системы кова­риационной матрицы, рассчитанной для подмножества блоков, имеющих наибольшие соответствующие собственные значения (метод Карунена-Лоева) и т.п. Решение во­проса о том, осуществлять ли "расщепление" в данном подмножестве или нет, может быть принято из различных соображений, например, исходя из анализа величины дис­персии блоков в подмножестве.

Как видно, алгоритм LBG весьма гибок, и предполагает дальнейшую оптимизацию в конкретном применении.

Недостатком алгоритма LBG является то, что большой объем необходимых для его исполнения вычислительных операций не поддается ни сокращению, ни распаралле­ливанию: на каждой итерации в первой процедуре приходится перебирать все блоки исходного изображения, сравнивая каждый из них со всеми элементами текущей кодо­вой книги, что не позволяет непосредственно применять LBG в системах реального времени.

Данный недостаток в значительной мере компенсируется тем, что в качестве предварительной кодовой книги можно использовать результат применения иных алгорит­мов (например, алгоритма Эквитца), используя LBG лишь для окончательной оптими­зации кодовой книги на малом количестве итераций без "расщеплений".

Алгоритм Эквитца

Данный алгоритм составления кодовой книги основан на последовательном сокращении (в противоположность LBG) числа элементов исходной кодовой книги.

При этом в качестве исходной кодовой книги используется само исходное изображение. Сокращение осуществляется путем поиска пары элементов текущей кодовой книги, менее всего отличающихся друг от друга в смысле некоторой меры, с после­дующей заменой такой пары блоком, полученным попиксельным арифметическим ус­реднением значений яркости в этой паре.

Эту операцию осуществляют до тех пор, пока размер кодовой книги не станет равен требуемому значению.

Алгоритм Эквитца более благоприятен с вычислительной точки зрения, чем LBG, но уступает ему по качеству получаемой кодовой книги.

Намного меньших объемов вычислительных операций требуют алгоритмы, основан­ные на принятии в качестве элемента кодовой книги собственных векторов ковариаци­онных матриц, рассчитанных для последовательностей блоков исходного изображе­ния. При этом получаются кодовые книги, как правило, нуждающиеся в уточнении ме­тодом LBG.

В связи с проблемой поиска элемента кодовой книги, наилучшим образом сходного с блоком исходного изображения, следует заметить, что в алгоритмах, использующих метод Карунена-Лоэва, параллельно с созданием самой кодовой книги происходит по­строение системы многомерных плоскостей (гиперплоскостей), делящих пространство изображений на ячейки, так что поиск соответствия блока исходного изображения эле­менту кодовой книги из полного перебора кодовой книги превращается в бинарный поиск соответствующей ячейки.

При этом поиск осуществляется путем вычисления знаков скалярных произведений векторов-нормалей, опущенных из точки-блока на упомянутые выше гиперплоскости и характеристических векторов этих гиперплоскостей. При этом количество операций на блок снижается со значения порядка k до .

Хочется заметить, что даже самые эффективные по скорости обработки варианты векторного квантования намного сложнее алгоритмов сжатия видеоинформации, использующих ортогональные преобразования, или, тем более, предсказания, что за­трудняет их применение в кодерах, работающих в реальном времени. Восстановление же закодированного с помощью векторного квантования изображения, наоборот, осуществляется намного проще, чем в любых других методах группового кодирования и требует (в простейшем варианте) лишь одного косвенного обращения к памяти на пиксель, или одного умножения с накоплением на пиксель, если перед подачей на кодер векторного квантования изображение было отнормировано по яркости и контрасту (с передачей соответствующих коэффициентов).

Очевидным фактором, лимитирующим общую достижимую степень сжатия при векторном квантовании, является необходимость передавать изображения – элементы кодовой книги, причем без потери информации при возможной упаковке. Таким обра­зом, большей эффективности векторного квантования можно ожидать в тех случаях, когда одна и та же кодовая книга может считаться оптимальной для аппроксимации как можно большего количества блоков.

Вместе с тем, существует теоретическая и, как оказалось, практическая возмож­ность обойти проблему передачи кодовых книг, при использовании так называемого фрактального сжатия (см. далее).

Еще одним специфическим вариантом блочного кодирования является использова­ние неунитарного интерполяционного преобразования.

При этом изображение разбивается на блоки, скажем 4х4 пикселей X(i, j), i, j=0, .., 3 – соответственно обозначения номеров строки и столбца.

Алгоритм передачи для каждого блока определяется, например, следующим обра­зом:

- значение Х(0, 0) передается непосредственно,

- величина Х(3, 3) передается путём её предсказания по переданному значению Х(0,0),

- величины Х(0, 3) и Х(3, 0) предсказываются по значению [Х(0,0) + Х(3,3)]/2.

Значения остальных пикселей передаются с предсказанием по 4-м пикселам.

Такой алгоритм существенно более прост в вычислениях, чем рассмотренные ранее унитарные преобразования.

При обзоре различных методов кодирования следует упомянуть также о методе, имеющем название "пирамида Лапласа", который стоял у истоков метода вейвлетного сжатия. В этом случае изображение расщепляется при помощи полосовых фильтров пространственных частот так, что границы (одни и те же по вертикали и по горизонтали) составляют гармонический ряд:

f_гр; f_гр*k; f_гр/k²;…

Обработка таких изображений-диапазонов состоит в передискретизации с прорежи­ванием в k-раз по вертикали и по горизонтали, а суммарное сжатие получается благо­даря тому, что спектральная мощность сигнала изображения падает с ростом частоты, а также из-за меньшей субъективной заметности ошибок квантования более высоко­частотных составляющих изображения. Возможно использование различных модификаций этого метода.

Стандарт JPEG

Целью разработки группой JPEG (Joint Photographic Expert Group), созданной при Международной организации по стандартам (ISO) при сотрудничестве с МККТТ, было создание первого международного стандарта сжатия полутоновых и цветных изображе­ний. При этом предполагалось выполнение следующих требований:

1) возможности адаптивного выбора параметров для оптимизации соотношения сжатие - качество восстановленного изображения в самом широком диапазоне;

2) универсальности процедуры обработки изображений любых размеров, с любой цветовой гаммой; не должно быть ограничений по сложности сюжета и статистическим свойствам;

3) приемлемой сложности вычислений преобразования изображений, реализуемых на компьютерах различной мощности с соответствующим программным обеспечением;

4) наличием следующих операционных режимов программы сжатия:

- пространственно-поступательной обработки, при которой изображение, возможно разбитое на блоки, обрабатывается слева направо и сверху вниз;

- обработки с последовательным углублением четкости, при которой наблюдатель получает на экране сначала грубое приближение, а затем программа осуществляет циклическое сканирование изображения, с каждым циклом повышая его четкость, добавляя высокочастотные компоненты;

- возможности сжатия без потерь, гарантирующего полное восстановление информации о каждом пикселе при обратной обработке, даже если степень сжатия оказы­вается небольшой;

- обеспечения многоуровневого кодирования, при котором четкость изображения связана не только с пространственно-частотными диапазонами (например, номера­ми Z-упорядоченных компонент унитарного преобразования), но и с уровнем точно­сти передачи (или номером бита двоичного представления величин передаваемых компонент).

В соответствии с этими требованиями стандарт JPEG не содержит указаний выпол­нения жесткой последовательности операций обработки, а предполагает их выбор по желанию пользователя.

Исходное изображение в соответствии со стандартом может быть многокомпонент­ным, где каждая i-ая компонента представляет собой прямоугольный массив данных с размерностью X_iY_i причем X_i и Y_i не могут превышать величину 2¹⁶.

Разрядность величин каждого элемента всех компонент перед подачей на кодек должна быть одинакова и равна N битам:

• 8 или 12 для кодека с дискретным косинусным преобразованием (ДКП);

• от 2 до 16 для дифференциального кодека (ДИКМ).

Сами величины элементов должны быть целыми числами от 0 до 2^N-1.

В стандарте JPEG оговаривается, что сжатие изображений может осуществляться либо с помощью ДКП двумерных блоков 88 пикселей, либо с помощью ДИКМ.

Ко всем компонентам изображения во время обработки должно применяться одно и то же преобразование. ДИКМ может осуществлять предсказание с помощью восьми различных масок по одному, двум или трем отсчетам:

№ МАСКИ	ФОРМУЛА ПРЕДСКАЗАНИЯ
0	0;
1	X(i-1,i);
2	X(i,j-1);
3	X(i-1,j-1);
4	X(i-1,J)+X(i,j-1)-X(i-1,j-1);
5	X(i-1,j)+[X(i,j-1)-X(i-1,j-1)]/2;
6	X(i,j-1)+[X(i-1,j)-X(i-1,j-1)]/2;
7	[X(i-1,j)+X(i,j-1)]/2.

Конкретный выбор того или иного быстрого алгоритма вычисления ДКП оставлен на усмотрение разработчиков прикладных программ.

Результат вычисления ДКП подвергается квантованию в соответствии с известной формулой

Fq(u,v) = round {F(u,v)/Q(u,v)},

где Q(u,v) - таблица коэффициентов квантования, разных для различных коэффициен­тов ДКП и различных компонент изображения.

Выбор и применение конкретных таблиц коэффициентов квантования оставлен на усмотрение пользователей, поскольку они могут быть оптимизированы для конкретных прикладных программ. Однако, стандарт JPEG требует применения для всех блоков каждого массива компонент изображения одной и той же таблицы квантования. Группой JPEG эмпирически получено несколько таблиц квантования.

Использование таблиц квантования позволяет получить более высокое качество восстанавливаемых изображений при одной и той же степени сокращения избыточно­сти информации.

После квантования компоненты ДКП в каждом блоке должны подвергаться Z-упорядочиванию. Величина Fq(0, 0) заменяется разностью с соответствующей величиной из предыдущего (при сканировании слева направо по массиву) блока.

В таком виде данные подаются на хаффмановский кодер. Также в качестве допол­нительной возможности стандарт предусматривает использование арифметического кодера, что позволяет дополнительно сократить объем на 8-10 %.

Рассмотрим более общий случай сжатия цветных изображений, каждый пиксель которых представлен 3-мя байтами, по байту на красный(R), зеленый(G) и синий(В) цвета. Кодирование начинается с того, что изображение разбива­ется на отдельные блоки размером 1616 отсчетов каждый, кото­рые затем кодируются (сжимаются) независимо друг от друга.

Далее, в каждом блоке от 3-х матриц спектральных коэффици­ентов для красной (R), зеленой (G) и синей (В) компонент изобра­жения, осуществляют переход к 3-м матрицам, представляющим яркостную (Y) и две цветностных (Сb) и (Сr) компоненты изображе­ния (содержат только информацию об их цвете и его насыщенности). Переход к компонентам (Сb) и (Сr) выгоден, так как позволяет при их кодировании использовать меньшее количе­ство отсчетов в блоке и за счет этого получить дополнительное сжатие.

Y = О,299R + 0,587G + 0,11B,

Cb= О,168R- 0,331G + 0,5R,

Cr = 0,5R-0,418G +0,0813B.

Затем матрица, представляющая яркостную компоненту и име­ющая размер 16x16 отсчетов, разделяется на 4 матрицы размером 88 отсчетов каждая, а две цветностных матрицы (Сb) и (Cr) путем прореживания по строкам и столбцам преобразуются в две цветно­стных матрицы (Сb) и (Cr) размером 88. При прореживании этих матриц из них исключаются каждая вторая строка и каждый вто­рой столбец. Такое преобразование оказывается допустимым, по­скольку наше зрение имеет понижен­ную остроту при наблюдении чисто хроматических изображений. На этом этапе в кодируемое изоб­ражение вносятся необратимые искажения за счет прореживания (происходит потеря информации) и происходит сжа­тие данных в два раза. До прореживания полное ко­личество отсчетов, которыми представлен блок изображения, равнялось 31616=768, а после – только 384.

Далее каждый из отсчетов шести матриц размером 88 отсче­тов подвергается ДКП, квантованию на 4096 уровней и записыва­ется 12-разрядным двоичным кодом. При этом получаем шесть матриц спектральных коэффициентов, 4 из которых представляют собой компоненту (Y), а две – компоненты (Сb) и (Сr). На этапе квантования достигается основное сжатие данных благо­даря тому, что спектральные коэффициенты с большими индекса­ми, на долю которых приходится малая доля энергии изображения, квантуются на малое число уровней (или усекаются), и, следовате­льно, на их представление затрачивается мало двоичных единиц ко­да. На этом этапе также происходит упоминавшаяся ранее потеря информации, так как в изображение вносятся необратимые искаже­ния (шум квантования). Сам процесс квантования заключается в том, что матрица спектральных коэффициентов целочисленно поэ­лементно делится на матрицу квантования, имеющую такую же размерность, т.е. 88. При этом значение проквантованного спект­рального коэффициента определяется

,

где исходное, не квантованное, значение спектрального коэффициента, а – соответствующий ему по положению в матрице элемент матрицы квантования. Матрица квантования Q по­строена по зональному принципу, составляющие ее числа представ­ляют собой величины равные 2^(12-m), где т – число уровней, на которое квантуется спектральный коэффициент, входящий в соот­ветствующую зону. Эта процедура интересна тем, что деление обес­печивает приведение спектральных коэффициентов к значениям од­ного порядка, а округление обеспечивает собственно квантование по уровню. После выполнения операции квантования мы получаем матрицу проквантованных спектральных коэффициентов F_кв, осо­бенностью которой является наличие большого количества малых и нулевых спектральных коэффициентов, расположенных преиму­щественно в правом нижнем углу матрицы. При восстановлении сжатого изображения значения проквантованных спектральных ко­эффициентов умножаются поэлементно на значения соот­ветствующих коэффициентов матрицы квантования _.

Следующий шаг алгоритма сжатия состоит в преобразовании полученной матрицы квантованных спектральных коэффициентов 88 в вектор из 64 элементов, в котором малые и нулевые спект­ральные коэффициенты должны быть по возможности сгруппиро­ваны. Эта цель достигается путем применения так называемого зиг­заг-сканирования (Z-упорядочивания), поскольку в начале считываются спектральные коэффициенты с большими амплитудами, а в конце – спектральные коэффициенты, величина которых мала или равна нулю, получающаяся в результа­те этого сканирования последовательность чисел будет в конце со­держать длинные последовательности нулей. Эта особенность ис­пользуется для дальнейшего сжатия данных путем энтропийного кодирования, которое состоит в последовательном применении метода кодирования длин серий и кода Хаффмена. Из ряда спект­ральных коэффициентов образуются пары чисел, одно из которых равно значению ненулевого спектрального коэффициента, а дру­гое – количеству предшествующих этому спектральному коэффи­циенту нулей. Полученные пары сжимаются посредством примене­ния кода Хаффмена с фиксированной таблицей. В этой таблице наиболее вероятным значениям полученных чисел, которые соот­ветствуют малым последовательностям нулей и малым значениям ненулевых спектральных коэффициентов ставятся в соответствие короткие коды. Поскольку код Хаффмена является префиксным, то не требуется никаких разделителей между кодовыми словами.

Алгоритм декодирования повторяет все перечисленные опера­ции в обратном порядке.

Достоинством описанного метода является высокая степень сжатия данных, которая для цветных изображений может дости­гать 6 – 10. Величина сжатия изображений при их записи в файл может регулироваться посредством специальной опции, при реали­зации которой соответствующим образом изменяются коэффициен­ты матрицы квантования Q. С помощью этой регулировки устанав­ливается допустимая степень ухудшения сжимаемого изображения, как, например, это сделано в графическом редакторе PhotoShop. Чем большая степень сжатия выбрана, тем большие искажения бу­дут в восстановленном изображении. В настоящее время этот метод сжатия данных широко применяется практически во всех графических ре­дакторах.

Следует иметь в виду, что при использовании сжатия по JPEG в исходное изображе­ние вносится весьма большое количество различного рода искажений, которые наибо­лее отчетливо проявляются при больших степенях сжатия. Рассмотрим класси­фикацию этих искажений.

1. Блокинг-эффект (Blocking-Effect). Характерное разбиение всего изображения на квадратные блоки с заметными границами. Блокинг-эффект возникает вследствие деления изображения на блоки с последующим их независимым кодированием, в ко­тором используется дискретное косинусное преобразование (ДКП) и квантование ко­эффициентов. Характерной особенностью ДКП с учетом квантования коэффициентов является возникновение ненулевых ошибок на границах блоков, которые идентифици­руются глазом как скачки яркости от одного блока к другому.

2. Мозаичный эффект (Mosaic Pattern) . Мозаичный эффект выглядит подобно блокинг-эффекту, но обуславливается не резкими переходами между различными блока­ми, а заметным глазу различием всей информации в соседних блоках. Можно также определить мозаичный эффект как остаточный блокинг-эффект после низкочастотной фильтрации изображения. Несмотря на то, что переходы между блоками становятся плавными, глаз воспринимает изображение как разбитое на блоки. Мозаичный эф­фект также возникает при слишком грубом квантовании коэффициентов ДКП, при ко­тором изображения внутри соседних блоков сильно отличаются друг от друга.

3. Размытие изображения (Blurring). При большом коэффициенте сжатия наблюда­ется размытие изображения, обусловленное значительным ограничением, либо пол­ным занулением высокочастотной части спектра ДКП. Мелкие детали становятся либо размытыми, либо полностью пропадают в изображении.

4. Окантовки на границах (Ringing). Этот тип искажений проявляется как появление характерных окантовок на резких переходах яркости изображения, обусловленных отсутствием высокочастотных компонентов спектра, либо значительным их искажением. Поскольку ступенчатый сигнал содержит большое количество спектральных компонен­тов (амплитуда которых убывает лишь обратно пропорционально их номеру), измене­ния амплитуд ДКП вследствие квантования могут нарушить монотонность функции вблизи ступеньки, что визуально проявляется как колебания яркости на резких перехо­дах.

5. Размытие цветов (Color Bleeding). Размытие цветов имеет такую же причину, что и эффект окантовки на границах, но проявляется на участках изображения с резкими скачками в сигнале яркости.

6.Искажение типа «ступеньки» (Staircase Effect). Данные искажения возникают как результат неправильного восстановления или передачи краев изображений внутри блоков. При рассмотрении каждого блока в отдельности граница, проходящая по неко­торому числу блоков, выглядит нормально. Иными словами, часть границы внутри блока визуально воспринимается правильно. Тем не менее, при переходе к следую­щему блоку граница объекта терпит скачок и, в целом, выглядит как «ступенька» с элементами, параллельными границам блоков. Причиной возникновения данного эф­фекта является использование в качестве базиса разложения функций ДКП, построен­ных в декартовых координатах. Каждая из базисных функций имеет строго выражен­ную вертикальную и горизонтальную ориентации. Поэтому при грубом квантовании ко­эффициентов ДКП на наклонной границе проявляется внутренняя ориентация базис­ных функций по осям координат. Следует отметить, что данный эффект проявляется, как правило, при воспроизведении восстановленного изображения в увеличенном масштабе.

9.4. Фрактальное и вейвлетное сжатие изображений

Фрактальные методы кодирования изображений

Фрактальные методы сжатия можно рассматривать как модификацию векторного квантования, при которой в качестве элементов кодовой книги используют блоки, вырезанные всевозможными способами из самого исходного изображения.

Представим себе некую процедуру, которая преобразует изображение некоторым выбранным способом. Например, этот способ предполагает уменьшение линейных размеров исходного изображения (рис. 9.11., слева) в два раза (рис.9.11., в центре) и тройное его копирование (рис. 9.11., справа).

Если этот процесс повторять итеративно несколько раз, то возникающие из различ­ных исходных изображений рисунки станут похожими друг на друга (рис. 9.12.).

При достаточно большом количестве итераций эти рисунки перестанут различаться. Это конечное изображение обладает рядом интересных свойств. Во-первых, оно не зависит от начального изображения, поскольку при достаточно большом числе итераций исходное изображение уменьшится до точки.

Рис.9.11. Способ фрактального преобразования изображения

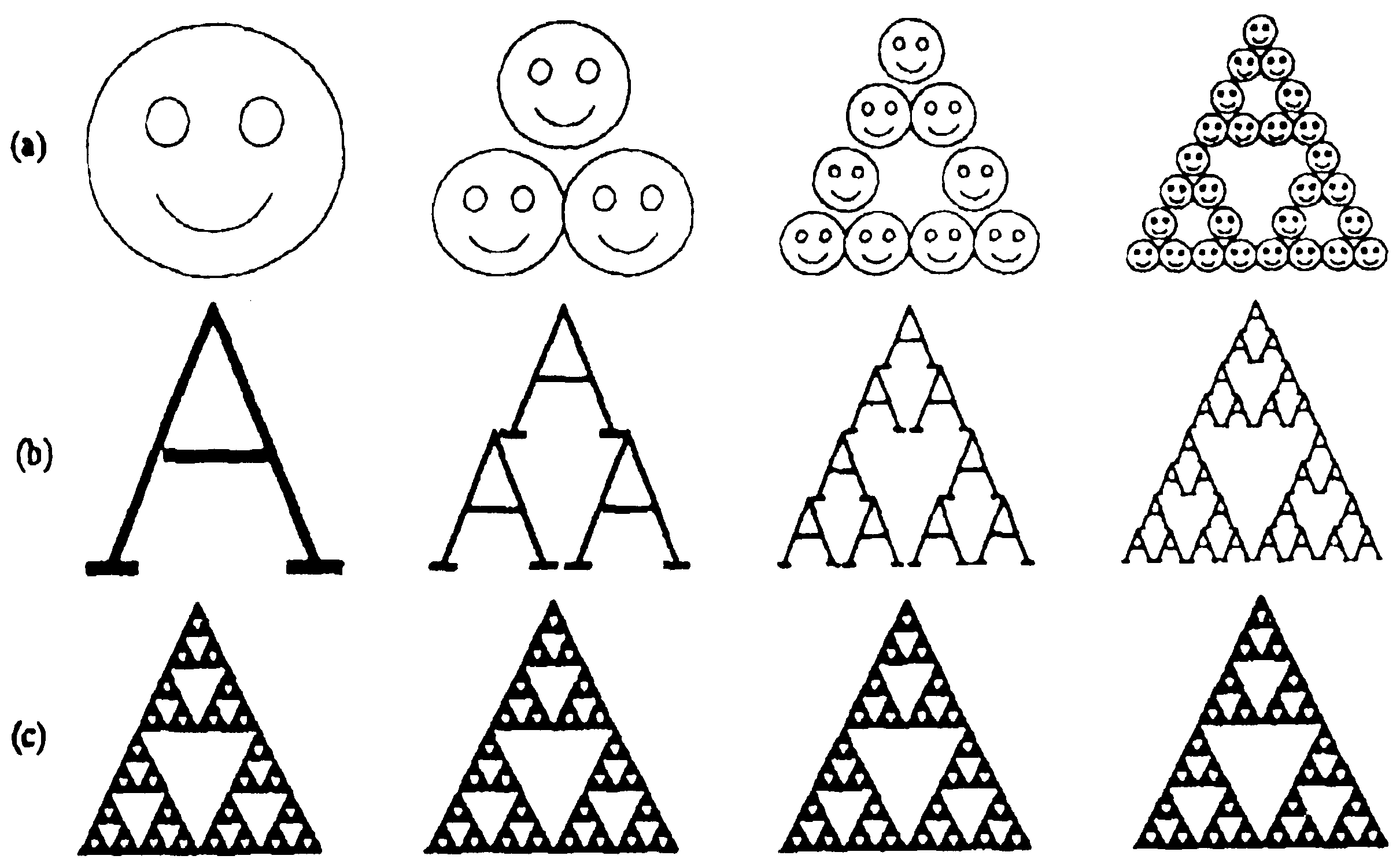
Рис. 9.12. Фрактальное преобразование различных изображений

Во-вторых, оно определяется исключительно процедурой преобразования. В-третьих, дальнейшие преобразования будут преобразовывать его в самого себя. В-четвертых, оно может иметь сколь угодно мелкие детали. Изображения такого типа называются аттракторами, а преобразования - фракталь­ными.

Разумеется, процедуры преобразования могут быть и другие. Единственное ограни­чение – это требование сходимости изображения в указанном выше смысле. В против­ном случае, если две разные точки исходного изображения в результате последова­тельности преобразований не сойдутся в одну, то конечное изображение будет зави­сеть от исходного и не будет аттрактором.

На практике достаточно большое количество преобразований можно описать с помощью матричного уравнения, определяющего линейное преобразование координат х и у,

где - параметры преобразования.

Такие преобразования называются аффинными преобразованиями плоскости и могут переворачивать, вытягивать, вращать и масштабировать исходное изображение.

На рис. 9.13 показано несколько процедур преобразования и их аттракторов:

– в верхнем ряду - описанное выше преобразование;

– в среднем ряду - аналогичное преобразование при дополнительном повороте верхней детали;

– в нижнем ряду - более сложное преобразование с поворотом деталей на разные углы и их масштабированием.

Последний случай наиболее интересен и имеет название "папоротник Барнсли" (Bamsley). Этот внешне сложный рисунок получен за счет четырех аффинных преобразований, каждое из которых имеет шесть параметров (см. приведенное матричное уравнение).

Такие самоподобные рисунки называются фракталами. Если перемножить число преобразований (4), число параметров (6) и число бит под хранение каждого из пара­метров (например, 32) то получим 4632=768 бит - столько бит необходимо для хра­нения способа получения этого изображения.

В тоже время приведенное штриховое изображение (1 бит/пиксель) папоротника имеет разрешение 256256 пиксель. Для прямого хранения такого изображения необхо­димо 65536 бит. То есть рассматриваемая схема позволяет "сжать изображение" при­мерно в 85 раз.

Рассмотрим условность такого определения коэффициента сжатия. Дело в том, что для хранения алгоритма преобразования требуется опреде­ленное, заранее известное, количество бит, но этот алгоритм позволяет создать изо­бражение любого размера с достаточно мелкими деталями, для хранения которого требуется другое (возможно существенно большее) количество бит. Соответственно размеру изображения будет меняться и коэффициент сжатия.

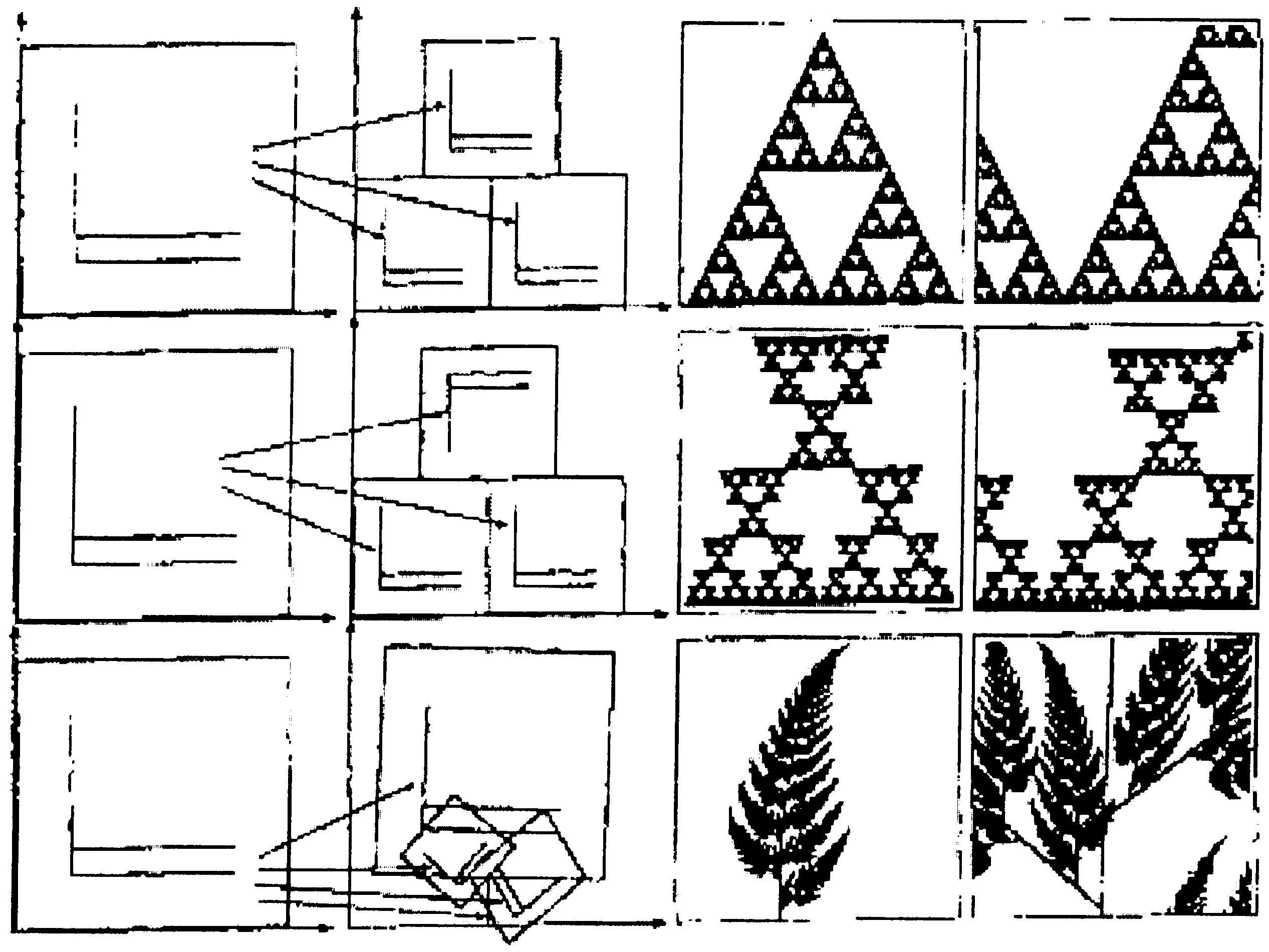
Рис. 9.13. Различные фрактальные преобразования изображения

Часто встречающиеся в реальной жизни изображения, как правило, нельзя считать аттракторами, однако они практически всегда содержат подобные детали. Например, в изображении Lena (Рис. 9.14.) можно выделить следующие подобные де­тали: участок контура плеча, контур отражения шляпы в зеркале и др.

Рис. 9.14. Тестовое изображение Lena (256 grayscale)

Возникает вопрос: можно ли для любой детали изображения подобрать деталь, ко­торая после некоторых преобразований станет достаточно похожей на исходную? Строгое математическое доказательство этого отсутствует, однако практика пока­зывает, что это возможно практически во всех случаях. Такие преобразования для полутоновых монохромных изображений можно фор­мально описать следующим образом.

Пусть яркость пикселей изображения z задана некоторой функцией z=f(x,y), где х, у – координаты пикселей.

Положим, z может иметь 256 фиксированных уровней. Само аффинное преобразова­ние i-ого блока полутонового изображения будет выглядеть следующим образом:

,

где – параметры аффинного преобразования, – коэффициенты преобразования контраста и яркости блока.

Теперь необходимо разбить исходное изображение на блоки (назовем их домена­ми), для которых будут подбираться подобные блоки (ранговые области).

Весьма часто используется один из самых простых способов разбиения и преобразования исходного изображения. Он заключается в следующем. Исходное изображение разбивается на квадратные домены, например, 44 пиксела. Затем для каждого домена подбирается ранговая область следующим образом.

Берется квадрат, например, в два раза большего размера (88) и путем усреднения по четырем соседним пикселам из него формируется квадрат 44. Этот квадрат ориентируется в одном из восьми различных положений: четыре положения определяются его поворотом на 90 градусов и еще четыре – поворотом на 90 градусов его зеркально­го отражения.

После преобразования контраста (путем умножения на некоторое число значений яркости каждого пиксела) и яркости (путем увеличения/уменьшения яркости каждого пиксела на некоторую величину) каждый из полученных квадратов сравнивается с до­меном.

При минимальном различии в среднеквадратичном смысле квадрат считается ран­говой областью рассматриваемого домена.

Вычисление оптимальных коэффициентов преобразования контраста и яркости квадратов путем минимизации среднеквадратичной разности яркостей пикселей доме­на и кандидата в ранговую область может быть произведено по следующим форму­лам:

где - яркости k-ых пикселей i-ой ранговой области и домена,

n – число пикселей в домене.

В этом случае среднеквадратичное отклонение яркостей домена и ранговой области может быть определено формулой

Такие операции проводятся по всем восьми возможным ориентациям квадрата. Для определения истинной ранговой области данного домена необходимо перебрать все возможные квадраты 88 изображения.

С этой целью вместо исходного квадрата используется квадрат, смещенный снача­ла по горизонтали на один пиксель, затем по вертикали на один пиксель и таким образом перебираются все возможные варианты. В каждом конкретном случае при этом про­цесс преобразования и сравнения повторяется. Номер ориентации, коэффициенты преобразования контраста и яркости, положение верхнего левого угла кандидата в ранговую область и среднеквадратичные отклонения фиксируются, а затем ранговая область выбирается по наименьшей величине из всех указанных отклонений.

Результат определяет ранговую область для данного домена.

Вейвлетное сжатие изображений

Термин "вейвлет" (дословный перевод – маленькая волна) появился сравнительно недавно – его ввели Гроссман и Морле (Grossman & Morlet) в середине 80-х годов в связи с анализом свойств сейсмических и акустических сигналов. В настоящее время семейство анализаторов, названных вейвлетами, начинает широко применяться в задачах распознавания образов; при обработке и синтезе различных сигналов, например, речевых; при анализе изображений самой различной природы (это могут быть изображение радужной оболочки глаза, рентгенограмма почки, спутниковые изображения облаков или поверхности планеты, снимок минерала и т.п.); для изучения свойств турбулентных полей; для свертки (упаковки) больших объемов информации и во многих других случаях.

Вейвлет-преобразование одномерного сигнала состоит в его разложении по базису, сконструированному из обладающей определенными свойствами солитоноподобной функции (вейвлета) посредством масштабных изменений и переносов. Каждая из функций этого базиса характеризует как определенную пространственную (временную) частоту, так и ее локализацию в физическом пространстве (времени).

Таким образом, в отличие от традиционно применяемого для анализа сигналов преобразования Фурье, вейвлет-преобразование обеспечивает двумерную развертку исследуемого одномерного сигнала, при этом частота и координата рассматриваются как независимые переменные. В результате появляется возможность анализировать свойства сигнала одновременно в физическом (время, координата) и в частотном пространствах. Сказанное легко обобщается на неодномерные сигналы или функции.

Область использования вейвлетов не ограничивается анализом свойств сигналов и полей различной природы, полученных численно, в эксперименте или при наблюдениях. Вейвлеты начинают применяться и для прямого численного моделирования – как иерархический базис, хорошо приспособленный для описания динамики сложных нелинейных процессов, характеризующихся взаимодействием возмущений в широких диапазонах пространственных и временных частот.

Известны трудности, встречающиеся при обработке коротких высокочастотных сигналов или сигналов с локализованными частотами. Вейвлет-преобразование оказывается очень удобным инструментом для адекватной расшифровки таких данных, поскольку элементы его базиса хорошо локализованы и обладают подвижным частотно-временным окном.

Далеко не случайно многие исследователи называют вейвлет-анализ "математическим микроскопом" – название прекрасно отражает замечательное свойство метода сохранять хорошее разрешение на разных масштабах. Способность этого "микроскопа" обнаружить внутреннюю структуру существенно неоднородного объекта и изучить его локальные скейлинговые свойства продемонстрирована на многих примерах.

Сжатие данных при записи или передаче изображений на основе вейвлет-преобразования относится к группе методов с потерей информации. Этот метод обеспечивает высокую степень сжатия, благодаря тому, что в нем учитываются свойства зрения и этот учет позволяет устранять из изображения те его детали (терять информацию), которые все равно зритель не замечает. В основе метода лежит вейвлет-преобразование изображения, при этом изображение рассматривается как результат суперпозиции особого вида базисных функций – вейвлет пакетов. Особенностью этих пакетов является то, что все они получаются из одной прототипной волны путем ее растяжения (или сжатия) и смещения. Эту прототипную волну можно рассматривать как импульсную функцию базового фильтра. При таком подходе вейвлет-преобразование можно рассматривать как совокупность процессов фильтрации и децимации. Поясним это примером вейвлет-преобразования черно-белого полутонового изображения, для чего обратимся к рис. 9.15. а, на котором приведено исходное изображение.

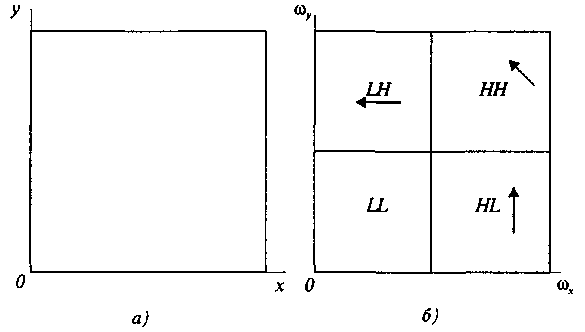
Рис. 9.15. Исходное изображение (а) и его спектр (б)

В начале исходное изоб­ражение подвергается фильтрации посредством четырех цифровых фильтров, импульсные функции которых подобраны таким обра­зом, что они делят спектр исходного изображения на четыре рав­ные не перекрывающихся области, как это показано на рис. 9.15.б. Область спектра, которая обозначена через LL, представляет раз­мытую (расфокусированную) версию исходного изображения, а об­ласти, обозначенные через LH, HL и НН, – соответственно его вы­сокочастотные компоненты, которые имеют вид преимущественно горизонтальных, вертикальных и диагональных границ. Так как ширина каждой из четырех компонент спектра, полученных в ре­зультате фильтрации, в направлении каждой из осей и в два раза меньше, чем ширина спектра исходного изображения, то каж­дое из изображений, соответствующих этим компонентам спектра, в соответствии с теоремой отсчетов может быть представлено вдвое меньшим числом строк и вдвое меньшим числом отсчетов вдоль каждой строки. Поэтому все четыре изображения, полученные на выходе цифровых фильтров, без ущерба для содержащейся в них информации могут быть подвергнуты прореживанию путем устра­нения каждой второй строки и каждого второго отсчета в строке, а затем размещены на той же площади, что и исходное изображение. Сказанное поясняется рис. 9.16. На рис. 9.17 приведена функциональная схема, посредством которой могут быть выполнены описанные операции. На этом рисунке блоками, обозначенными через LL, LH, HL, НН представлены соответствующие цифровые фильтры, а бло­ками, обозначенными через 4, – устройства, осуществляющие прореживание профильтрованных изображений.

Рис. 9.16. Компоненты LL, LH, HL и НН исходного изображе­ния после прореживания

Рис. 9.17. Функциональная схема, осуществляющая одношаговое вейвлет-преоб­разование

Вейвлет-преобразование обратимо, используя четыре изображе­ния показанные на рис. 9.16, можно точно восстановить исходное изображение. Для этого сначала в каждый из компонентов изобра­жений LL, LH, HL, НН вставляются пропущенные строки, а также пропущенные в строках отсчеты, значения которых находятся пу­тем интерполяции, а затем эти компоненты суммируются путем на­ложения друг на друга. На рис. 9.18 приведена схема, реализующая эти действия, в которой блоками, обозначенными через 4, осуще­ствляется восстановление пропущенных строк и отсчетов в строках.

В приведенном примере рассмотрено одношаговое вейвлет-преобразование, но число шагов может быть и большим. На рис. 9.19 приведена схема, реализующая двухшаговое вейвлет-преобразо­вание, а на рис. 9.20 – компоненты изображения, полученные в ре­зультате этого преобразования. Способ восстановления изображе­ния из вейвлет компонентов в данном случае очевиден и пояснений не требует. До сих пор мы рассматривали разложение изображения на вейвлет компоненты и синтез из них исходного изображения, при этом, разумеется, никакого сжатия данных не происходило.

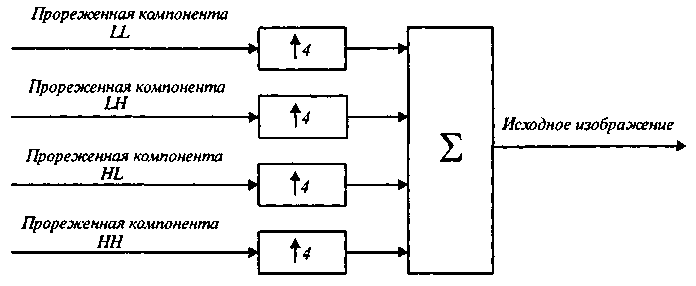
Рис. 9.18. Функциональная схема, восстанавливающая исходное изображение

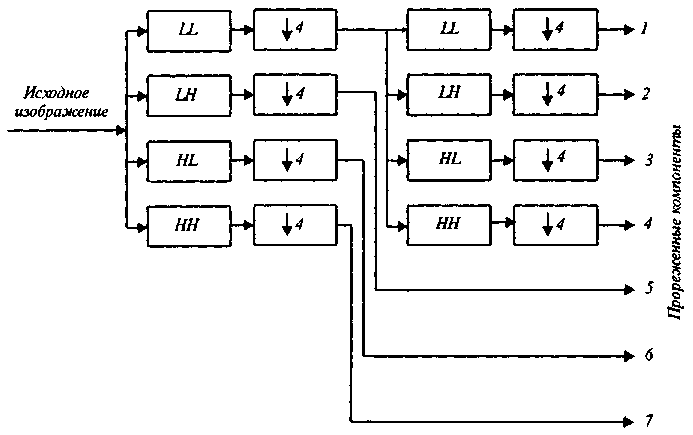
Рис. 9.19. Функциональная схема, осуществляющая двухшаговое вейвлет-преоб­разование

Обратимся теперь к рассмотрению метода сжатия данных на основе вейвлет-преобразований применительно к случаю сжатия черно-белого полутонового изображения. Этот метод в значитель­ной степени похож на метод сжатия данных используемый в JPEG и отличается от него лишь тем, что в JPEG квантованию на разное число уровней подлежат компоненты (спектральные коэффициен­ты), полученные в результате ДКП, в то время как в рассматривае­мом методе на различное число уровней квантуются компоненты, полученные в результате вейвлет-преобразований.

Рис. 9.20. Компоненты исходного изображения после двух шагового вейвлет-преобразования

И в том, и в другом случае используется особенность нашего зрения, заключающаяся в том, что оно мало чувствительно к шуму квантования высокочастотных компонент изображения. Однако, благодаря тому, что при использовании вейвлет-преобразований исходное изображение не разбивается на отдельные блоки, в восстановленном после силь­ного сжатия изображении отсутствуют такие неприятные артефак­ты (искажения), как заметность блочной структуры. В рассматрива­емом методе процедура сжатия начинается с того, что исходное изображение подвергается трехшаговому вейвлет-преобразованию, в результате которого получаются 10 компонент, показанных на рис. 9.21. Затем каждая компонента квантуется, причем высокочас­тотные компоненты квантуются на меньшее число уровней, высо­кочастотные – на большее. Например, отсчеты компонент 8, 9, 10 можно проквантовать на два уровня, отводя для их представления всего одну единицу двоичного кода, отсчеты компонент 5, 6, 7 – на 4 уровня, выделяя на их представление две двоичных единицы кода, отсчеты компонент 2, 3, 4 – на восемь уровней, расходуя на их представление три двоичных единицы кода, и только отсчеты компоненты 1 должны быть проквантованы на 256 уровней с затра­той на представление каждого из них по 8 двоичных единиц.

Рис. 9.21. Компоненты исходного изображения после трехшагового вейвлет-преобразования

При квантовании отсчетов компонент, полученных в результате вейвлет-преобразований, на пониженное число уровней в них вносится шум квантования, т.е. имеет место потеря информации, но если сжатие не слишком велико, т.е. число используемых уровней квантования не слишком занижено, то эти шумы на восстановленном изображе­нии будут не заметны. В рассмотренном примере за счет экономии двоичных единиц кода на представление высокочастотных компо­нент вейвлет-преобразований мы получаем сжатие данных равное

Сам процесс квантования в данном случае так же, как и в случае JPEG, осуществляется путем деления матрицы отсчетов, показан­ной на рис 9.21, на матрицу квантования.

Далее проквантованные отсчеты подвергаются энтропийному кодированию аналогично тому, как это делается в JPEG, которое состоит в последовательном применении метода кодирования длин серий и кода Хаффмена (из ряда спект­ральных коэффициентов образуются пары чисел, одно равно значению ненулевого спектрального коэффициента, а дру­гое – количеству предшествующих ему нулей, которые сжимаются посредством примене­ния кода Хаффмена с фиксированной таблицей: наиболее вероятным значениям полученных чисел, которые соот­ветствуют малым последовательностям нулей и малым значениям ненулевых спектральных коэффициентов ставятся в соответствие короткие коды). В резуль­тате энтропийного кодирования получается дополнительное сжатие, которое составляет около 3-х раз.

При сжатии цветных изображений так же, как и в случае JPEG, имеет место дополнительное сжатие за счет пере­хода от системы (R), (G), (В) к системе (Y), (Сb) и (Сr) компонент с соответствующими прореживаниями, что дает в конечном итоге дополнительное сжатие данных в два раза. Результирующее сжатие данных, которое получается при использовании данного метода, достигает 30 – 50 раз. При большом сжатии данных этот метод также приводит к появлению артефактов на восстановленных изображениях в виде появления окантовок и по­сторонних узоров, однако, они менее неприятны, чем артефакты, возникающие при использовании других методов сжатия данных.

Интегральное преобразование Фурье и ряды Фурье являются основой гармонического анализа. Получаемые в результате преобразования коэффициенты Фурье поддаются достаточно простой физической интерпретации, причем простота ни в коем случае не умаляет важности последующих выводов о характере исследуемого сигнала.

Вейвлет-преобразование не так широко известно, поскольку применяется сравнительно недавно и математический аппарат находится в стадии активной разработки.

Разложение по вейвлетам

Рассмотрим пространство функций f(t), определенных на всей оси R(-,) и обладающих конечной энергией (нормой)

“Волны”, образующие пространство , должны стремится к нулю на  и для практических целей чем быстрее, тем лучше. Рассмотрим в качестве базисных функций вейвлеты – хорошо локализованные солитоно-подобные “маленькие волны” (дословный перевод слова wavelet). Сконструируем функциональное пространство с помощью одного вейвлета (t). Отметим, что это может быть вейвлет с одной частотой или с набором частот (frequency bands). Начнем с дискретных преобразований.

Наиболее просто покрытие всей оси R(-,) с помощью быстро стремящейся к нулю локализованной функции реализовать используя систему сдвигов (переносов) вдоль оси.

(9.2)

нормированы на единицу, т.е.

Вейвлет  называется ортогональным, если определенное соотношением (9.2) семейство представляет собой ортонормированный базис функционального пространства , т.е. и каждая функция f может быть представлена в виде ряда

(9.3)

равномерная сходимость которого в означает, что

Простейшим примером ортогонального вейвлета является HAAR-вейвлет, названный так по имени предложившего его Хаара (Haar), и определяемый соотношением:

(9.4)

Сконцентрируем базис функционального пространства с помощью непрерывных масштабных преобразований и переносов вейвлета (t) с произвольными значениями базисных параметров – масштабного коэффициента a и параметра сдвига b:

(9.5)

и на его основе запишем интегральное вейвлет-преобразование:

(9.6)

Коэффициенты разложения (9.3) функции f в ряд по вевлетам можно определить через интегральное вейвлет-преобразование:

Итак, каждая функция из может быть получена суперпозицией масштабных преобразований и сдвигов базисного вейвлета, т.е. является композицией "вейвлетных волн" (с коэффициентами, зависящими от номера волны (частоты, масштаба) и от параметра сдвига (времени)).

Использование дискретного вейвлет-преобразования (дискретного частотно-временного пространства в виде целых сдвигов и растяжений по степеням двойки) позволяет провести доказательство многих положений теории вейвлетов, связанных с полнотой и ортогональностью базиса, сходимостью рядов и т.п. Доказательность этих положений необходима, например, при сжатии информации или в задачах численного моделирования, т.е. в случаях, когда важно провести разложение с минимальным числом независимых коэффициентов вейвлет-преобразования и иметь точную формулу обратного преобразования. При применении вейвлетов для анализа сигналов непрерывное вейвлет-преобразование (9.6) более удобно; его избыточность, связанная с непрерывным изменением масштабного коэффициента а и параметра сдвига b, становится здесь положительным качеством, так как позволяет более полно и четко представить и проанализировать содержащуюся в данных информацию.

Обратное вейвлет-преобразование

Ортонормированность базисов пространства , построенных на основе вейвлетов, определяется и выбором базисного вейвлета, и способом построения базиса (значениями базисных параметров а, b).

Конечно же, вейвлет может считаться базисной функцией только в том случае, если построенный с его помощью базис ортонормирован и обратное преобразование существует. Однако строгие доказательства полноты и ортогональности сложны и громоздки. Кроме того, для практических целей часто достаточно бывает устойчивости и "приблизительной" ортогональности системы функций разложения, т.е. достаточно, чтобы она была "почти базисом". Как правило, для анализа сигналов используются такие "почти базисные" вейвлеты.

Приведем здесь обратное преобразование лишь для тех двух случаев, что описаны выше: для базиса (9.2), допускающего расширения и сдвиги и базиса (9.5), построенного при произвольных значениях (a b) с помощью того же базиса (9.5), что и прямое.

Функция  называется R-функцией, если базис , определенный выражением (9.2), является базисом Рисса (Riesz) в том смысле, что существуют две константы А и В, 0<AB<, для которых соотношение

выполняется при любой (ограниченной, дважды квадратично суммируемой) последовательности :

Для любой R-функции существует базис - “двойник” базиса (в том смысле, что , с помощью которого можно построить реконструкционную формулу

. (9.7)

Если  - ортогональный вейвлет и - ортонормированный базис, то и совпадают и формула (9.7) является формулой обратного преобразования. Если  - не ортогональный вейвлет, но является двухместным или парным R-вейвлетом (dyadic wavelet), то он имеет двойника , с помощью которого двойник семейства строится подобно базису(7): .

В общем случае реконструкционная формула (9.7) даже не обязательно является вейвлет-рядом в том смысле, что  не является вейвлетом и может не иметь базиса-двойника, построенного по типу (9.5).

Частотно-временная локализация

Преобразование Фурье и ряды Фурье являются прекрасным математическим аппаратом для физической интерпретации процессов при анализе характеризующих их сигналов. Однако иногда они оказываются недостаточно эффективными.

Чтобы получить спектральную информацию на выбранной частоте, необходимо иметь и прошлую, и будущую временную информацию; к тому необходимо учитывть, что частота может эволюционировать со временем. Преобразование Фурье, например, не отличает сигнал, представляющий собой сумму двух синусоид с разными частотами, от сигнала, состоящего из тех же синусоид, включающихся последовательно одна за другой.

Кроме того, известно, что частота сигнала обратно пропорциональна его продолжительности. Поэтому для получения высокочастотной информации с хорошей точностью важно извлекать ее из относительно малых временных интервалов, а не из всего сигнала; и наоборот – низкочастотную спектральную информацию извлекать из относительно широких временных интервалов сигнала.

Часть описанных трудностей снимается при использовании оконного преобразования Фурье. Однако бесконечно осциллирующая базисная функция (синусоидальная волна) не позволяет получать по-настоящему локализованную информацию. Элементом базиса вейвлет-преобразования является хорошо локализованная функция, быстро стремящаяся к нулю вне небольшого интервала, что позволяет провести "локализованный спектральный анализ". Иными словами, вейвлет-преобразование автоматически обладает подвижным частотно-временным окном, узким на малых масштабах и широким на больших.

Признаки вейвлета

Для практического применения важно знать признаки, которыми обязательно должна обладать функция, чтобы быть вейвлетом.

Локализация. Вейвлет-преобразование в отличие от преобразования Фурье использует локализованную базисную функцию. Вейвлет должен быть локализован и во временном пространстве, и по частоте.

Нулевое среднее. .Часто для приложений оказывается необходимым, чтобы не только нулевой, но и все первые m моментов были равны нулю: .

Такой вейвлет называют вейвлетом m-го порядка. Обладающие большим числом нулевых моментов вейвлеты позволяют, игнорируя наиболее регулярные полиноминальные составляющие сигнала, анализировать мелкомасштабные флуктуации и особенности высокого порядка.

Ограниченность. Оценка хорошей локализации и ограниченности может быть записана в виде , здесь - доминантная частота вейвлета, число n должно быть возможно большим.

Автомодельность базиса. Характерным признаком базиса вейвлет-преобразования является его самоподобие. Все вейвлеты данного семейства имеют то же число осцилляций, что и базисный вейвлет , поскольку получены из него посредствам масштабных преобразований и сдвигов. Благодаря этому вейвлет-преобразование с успехом применяется для анализа фрактальных сигналов.

Примеры вейвлетобразующих функций

Поскольку вейвлет-преобразование есть скалярное произведение анализирующего вейвлета на заданном масштабе и анализируемого сигнала, коэффициенты W(a,b) содержат комбинированную информацию об анализирующем вейвлете и анализируемом сигнале (как и коэффициенты преобразования Фурье, которые содержат информацию о сигнале и о синусоидальной волне).

Выбор анализирующего вейвлета, как правило, определяется тем, какую информацию необходимо извлечь из сигнала. Каждый вейвлет имеет характерные особенности во временном и в частотном пространстве, поэтому иногда с помощью разных вейвлетов можно полнее выявить и подчеркнуть те или иные свойства анализируемого сигнала.

Если продолжить уже упоминавшуюся аналогию с математическим “микроскопом”, то параметр сдвига b фиксирует точку фокусировки микроскопа, масштабный коэффициент a – увеличение и, наконец, выбором базисного вейвлета  определяются оптические качества микроскопа.

Вещественные базисы часто конструируются на основе произвольных функций Гаусса.

Более высокие производные имеют больше нулевых моментов и позволяют извлечь информацию об особенностях более высокого порядка, содержащихся в сигнале.

На рисунке 9.22.а, б показаны вейвлеты, полученные при m=1 и m=2 соответственно. Из-за их формы первый называют обычно WAVE-вейвлет, второй – MHAT-вейвлет, или “мексиканская шляпа”. MHAT-вейвлет, имеющий узкий энергетический спектр и два равных нулю момента (нулевой и первый), хорошо приспособлен для анализа сложных сигналов. Обобщенный на двумерный случай MHAT-вейвлет часто используется для анализа изотропных полей. Если же производная берется лишь в одном направлении, получается неизотропный базис с хорошей угловой избирательностью. Для построения такого базиса к масштабным преобразованиям и сдвигам базисного вейвлета необходимо добавить его вращение. При этом математический микроскоп (вейвлет-преобразование) приобретает еще и качества поляризатора с углом поляризации, пропорциональным углу поворота вейвлета.

Примеры комплексных вейвлетов приведены на рис. 9.22.в, г (показаны их действительные составляющие). Наиболее часто используемый комплексный базис строится на основе хорошо локализованного в k- и r-пространстве вейвлета Морле (Morlet). На рис 9.22.в вейвлет Морле показан для . С увеличением возрастает угловая избирательность базиса, но ухудшается пространственная.

Часто применяемый в квантовой механике вейвлет Пауля (Paul) показан на рис. 9.22.г для m=4 (чем больше m, тем больше нулевых моментов имеет вейвлет).

Представленные комплексные вейвлеты являются прогрессивными. Так называются вейвлеты, имеющие нулевые коэффициенты Фурье при отрицательных значениях волновых чисел. Они хорошо приспособлены для анализа сигналов, для которых важен принцип причинности: эти вейвлеты сохраняют направление времени и не создают паразитной интерференции между прошлым и будущим.

а)	б)	в)	г)	д)	е)

Рис. 9.22. Примеры часто используемых вейвлетов: (a) WAVE, (б) MHAT, (в) Morlet, (г) Paul, (д) LMB, (е) Daubechies. Показаны вейвлеты в зависимости от времени (верхняя строка) и их образы Фурье (нижняя строка)

Отметим, что при анализе комплексного одномерного сигнала или при использовании комплексного анализирующего вейвлета в результате вейвлет-преобразования получаются двумерные массивы значений модуля коэффициентов и фазы

На рисунке 9.22.д, е приведены примеры вейвлетов, которые часто служат основой для построения ортогональных дискретных базисов с помощью процедуры Малла (Mallat): LMB-вейвлет, предложенный Лемарье, Мейером и Бэтлом (Lemarie, Meyer, Battle) и один из вейвлетов Добеши. Это биортогональные вейвлеты, имеющие пару (двойника), необходимую для получения реконструкционной формулы.

Свойства и возможности вейвлет-преобразования

Одномерное преобразование Фурье дает также одномерную информацию об относительном вкладе (амплитудах) разных временных масштабов (частот). Результа­том вейвлет-преобразования одномерного ряда является двумерный массив амплитуд вейвлет-преобразования – значений коэффициентов W(a,b). Распределение этих значений в пространстве (a,b)=(временной масштаб, временная локализация) дает информацию об эволюции относительного вклада компонент разного масштаба во времени и называется спектром коэффициентов вейвлет-преобразования, (частотно-)масштабно-временным спектром или вейвлет-спектром (time-scale spectrum или вейвлет spectrum в отличие от single spectrum преобразования Фурье).

Способы представления результатов

Спектр W(a,b) одномерного сигнала представляет собой поверхность в трехмерном пространстве. Способы визуализации этой информации могут быть различными. Вместо изображения поверхностей часто представляют их проекции на плоскость аb с изолиниями или изоуровнями, позволяющими проследить изменение интенсивности амплитуд вейвлет-преобразования на разных масштабах и во времени, а также картины линий локальных экстремумов этих поверхностей (так называемый "sceleton"), четко выявляющие структуру анализируемого процесса. Термин "скелет" или "скелетон" хорошо отражает характер картин линий локальных экстремумов (см. примеры), и мы будем использовать его для краткости.

В тех случаях, когда необходимо показать очень широкий диапазон масштабов, визуализация результатов в логарифмических координатах, например, (log a,b) предпочтительнее, чем в линейных.

Несомненное преимущество применения этого преобразования - возможность представлять быстро изменяющиеся сигналы в компактной форме. Подобно широко используемому быстрому преобразованию Фурье (БПФ), вейвлет-преобразование обратимо и может служить инструментом анализа характеристик сигналов (спектральный анализ и др.). В отличие от БПФ (где базисными функциями служат синусы и косинусы) вейвлет-преобразования формируют «родительские функции» более сложной формы. Их исходный набор обеспечивает получение бесконечного числа новых форм функций. Поскольку, в отличие от синусов и косинусов, индивидуальные вейвлет-функции ограничены в пространстве, с их помощью можно локализовать пространственный объект с высокой степенью точности.

Дискретное вейвлет-преобразование воспроизводит конечное число коэффициентов для ограниченной временной или частотной области, а непрерывное вейвлет-преобразование – действительное значение функций времени и масштаба. Алгоритм быстрого пирамидального иерархического разложения сигнала в векторы данных половинной длины позволяет получить множество коэффициентов разложения (для разрешения 1/2, 1/4, 1/8 и т. д.). Cтепень сжатия при вейвлет-преобразовании зависит от необходимого разрешения.

Сегодня у специалистов не вызывает сомнения, что эти алгоритмы кодирования обладают рядом преимуществ по сравнению с алгоритмами, построенными на основе дискретного косинусного преобразования Фурье.

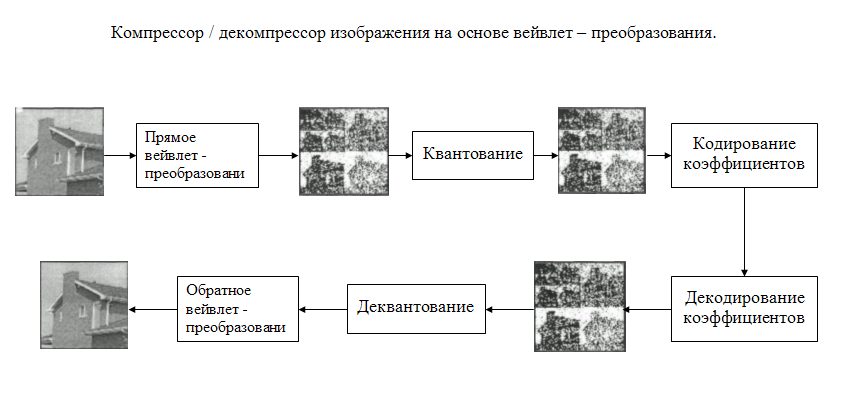
Исходное изображение	Village Размер 106663724 bit. Полноцветная картинка с реаль­ным количест­вом цветов 256120, получена сканированием репродукции картины. Основные признаки: много мелких деталей, встречаются как области с четко прорисованными границами объектов, так и области с размытыми границами, большое количество реально используемых цветов.
После вейвлет-сжатия (степень сжатия – 164)	После JPEG-сжатия (степень сжатия – 163.3)

Исходное изображение	Lena Размер 512512256 grayscale. Реальное число оттенков се­рого - 215. Очень популярно в Internet, наиболее широко применяется при тестировании кодекса, стало практически стандартом де-факто. Оригинал был напечатан в журнале Playboy за 1972 год. В дальнейшем было отскани­ровано и преобразовано в монохромный вариант.
После вейвлет-сжатия (степень сжатия – 145)	После JPEG-сжатия (степень сжатия – 135)

9. Красильников Н.Н. Цифровая обработка изображений – М.: Вузовская книга, 2001

10. Прэтт У. Цифровая обработка изображений, т.1, т. 2. - М.: Мир, 1982

11. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов./ Перевод с английского И.И.Грушко. - М.: Мир, 1989

12. Астафьева Н. М. Вейвлет-анализ: основы теории и примеры применения // Успехи физических наук. 1998. Т. 166. № 11.

13. Астафьева Н. М. Вейвлет-преобразования. Основные свойства и примеры применения. М.: ИКИ РАН. 1994. № 1891.

По данной теме предлагается выполнение курсового проекта. Выбранную тематику необходимо согласовать с преподавателем и получить у него задание на проектирование.

По этой теме является обязательным выполнение Лабораторной работы 2 «Методы сжатия изображений» и Лабораторной работы 3 «Применение алгоритма дифференциальной импульсно-кодовой модуляции (ДИКМ) в космических системах».

Предлагается пройти тест для самоконтроля (Тест 9) на усвоение материала. А также ознакомится с программой (Программа 7 «Алгоритм сжатия изображения (RLE–алгоритм)») и выполнить предложенное в ней задание. Программа, написанная в среде Delphi, предназначена для получения навыков в создании программного кода по работе с графическими файлами и содержит исходный код с комментариями.

10. Техническая реализация комплексов обработки информации

10.1. Управление процессами обработки и анализа изображений

Комплексный алгоритм обработки и анализа изображений

Информационные модели процессов