3.3 Числовые характеристики непрерывных случайных величин.

В качестве количественных показателей, характеризующих случайные величины, используются:

1) наиболее вероятное значение случайной величины;

2) её математическое ожидание;

3) показатель разброса измерений случайной величины около своего математического ожидания;

4) показатель, характеризующий асимметричность функции – закона распределения вероятностей.

Эти показатели могут быть определены следующим образом. Наиболее вероятное значение получим, решив уравнение . Математическое ожидание вычислим по формуле:

,

где – оператор математического ожидания.

Дисперсия, характеризующая разброс, равна математическому ожиданию квадрата отклонения случайной величины от своего математического ожидания

,

где – оператор определения дисперсии.

На рис. 3.3.1. показаны графики трех законов распределения: 1) симметричного, 2)асимметричного 1-ого рода, 3) асимметричного 2-ого рода.

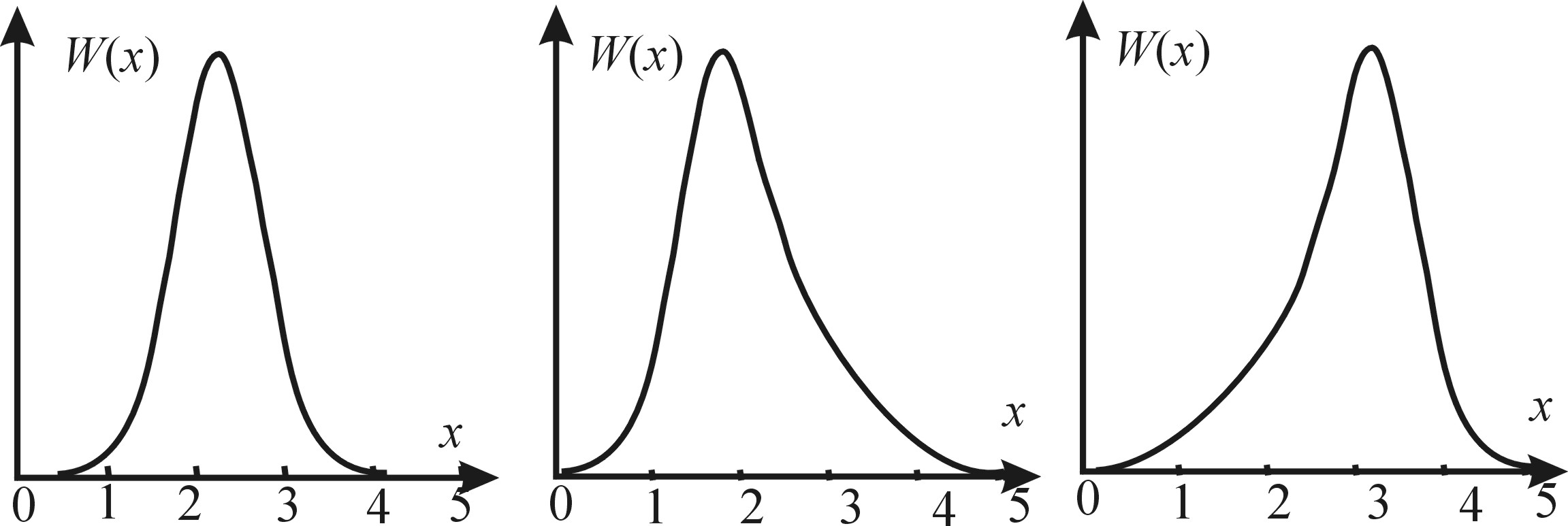
1) 2) 3)

Рис. 3.3.1. Симметричные и асимметричные законы распределения вероятностей.

В качестве показателя асимметрии используется коэффициент , вычисляемый по формуле

.

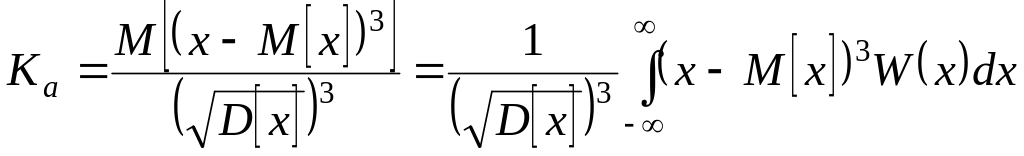Если , то и имеет место положительная асимметрия; если , то и имеет место отрицательная асимметрия. Эти показатели можно оценивать по экспериментальным измерениям. Оценка математического ожидания – это среднее значение измерений

Оценка дисперсии – это среднеквадратичное отклонение измерений от своего среднего

Оценка коэффициента асимметрии вычисляется по формуле

.

Располагая этими оценками, можно получать представления о виде законов распределения.

3.4 Двухмерные случайные величины

Рассмотрим случайное расположение точек на плоскости. В прямоугольной системе координат каждой j-ой точке соответствуют координаты . Множеству точек со случайным расположением (например, координаты пробоин в мишени) соответствует множество пар случайных измерений . Если всё пространство точек разделить на элементарные квадраты , и определить число точек , попадающих в квадрат , то можно оценить частоты попадания . Если число точек увеличивать до бесконечности, а элементарные квадраты до бесконечно малых , то вероятность попадания точек в бесконечно малую площадку равна произведению плотности распределения вероятности на бесконечно малую площадь .

Из этого дифференциального уравнения следует, что

Двухмерные закон и функция распределения вероятности обладают следующими свойствами:

1) функция всегда положительная и объём описываемой поверхности равен единице

2) функция неубывающая и равна

, .

Очевидными представляются следующие соотношения, вытекающие из свойств случайных величин x и y как случайных событий:

1) ,

2)

3) =

Из последних выражений следуют формулы Байеса для определения условных законов распределения

,

.

Кроме математических ожиданий и дисперсий случайных величин x и y числовыми характеристиками двумерных случайных величин являются условные математические ожидания

,

и условные дисперсии

, ,

где

Статистическая связь между случайными величинами характеризуется коэффициентом корреляции

.

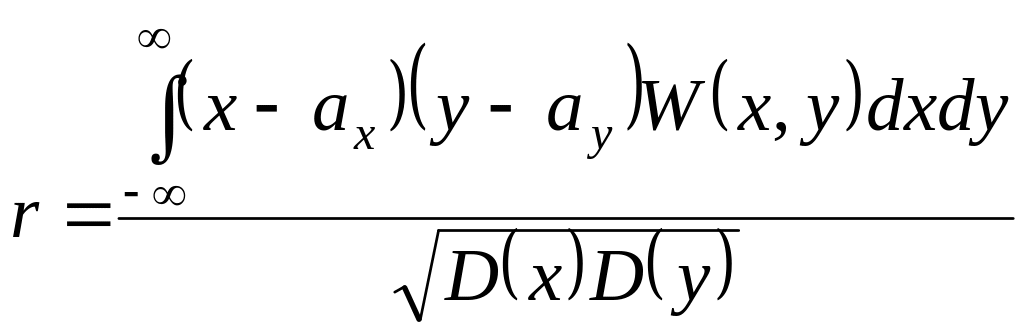На рис 3.4.1 показаны расположения точек со случайными координатами коррелированных случайных величин

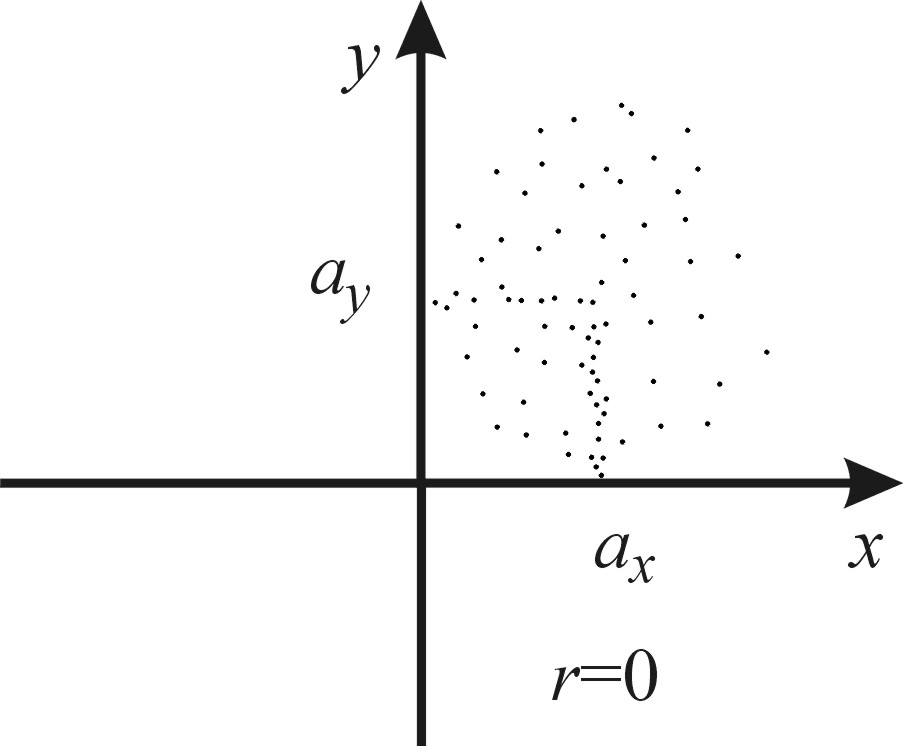
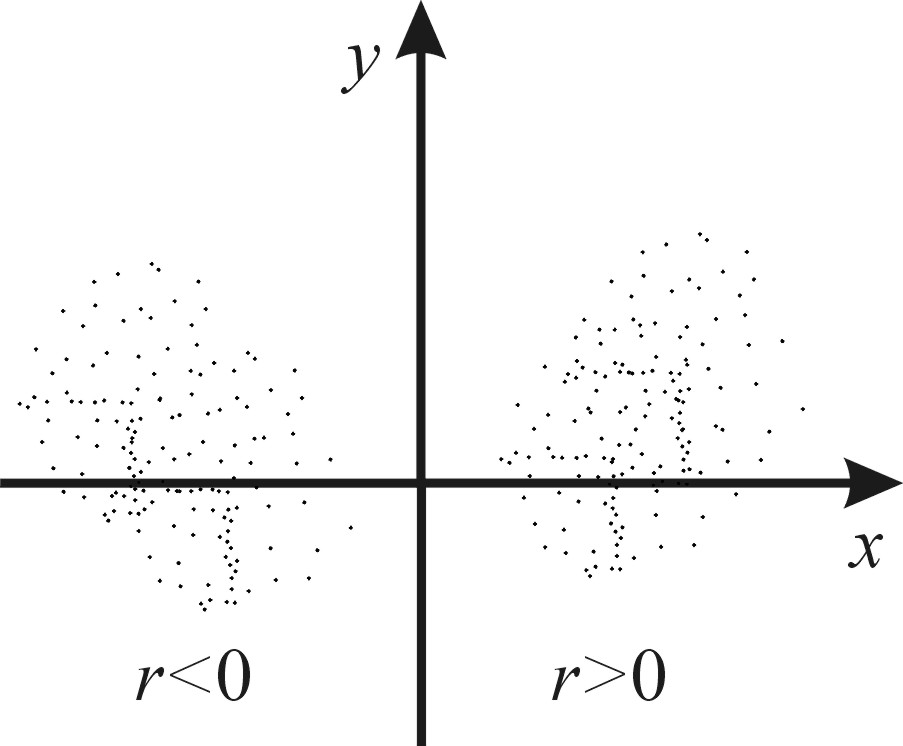
Рис 3.4.1 Случайные точки на плоскости xy.

Если случайные величины некоррелированные , то они статистически не связаны и в этом случае .

Коэффициент корреляции характеризует тесноту расположения чисел на плоскости. Очевидно, что при это связь функциональная . Коэффициент корреляции может изменяться от –1 до +1. При положительной корреляции с увеличением x возрастает y и при r < 0 наоборот, y уменьшается (рис.3.4.1). Например, вес и рост человека связаны положительной корреляцией, а время, затраченное студентами не на подготовку к экзамену и оценки на экзамене связаны отрицательной корреляцией.

Понятие некоррелированности не эквивалентно понятию независимости: две независимые случайные величины всегда некоррелированы. Обратное неверно: из некоррелированности случайных величин ещё не следует независимость. Убедимся в этом на следующем примере. Две независимые случайные величины x и y имеют равномерную плотность распределения в пределах окружности с радиусом D/2, где D – диаметр окружности.

, .

Зависимость от очевидна: если , то y может принимать любые значения от до , но если , то принимает одно единственное значение, равное нулю. Теперь вычислим их коэффициент корреляции по формуле

Интеграл можно разделить на 4 интеграла по секторам. Из них 2 будут положительные и 2 отрицательные. Их сумма будет равна ноль, т.е. в рассматриваемом случае и зависимые, но некоррелированные .