1.5. Статистическая теория последовательности зависимых случайных событий

Рассмотрим последовательность двух случайных событий S₁ и S₂, появляющихся в моменты времени , и обладающих следующими свойствами: вероятность появления событий S₁ и S₂ в момент времени t_k зависит от того, какое событие было в момент времени t_k-1. Обозначим эти переходные вероятности и , и . Очевидно, что вероятности появления событий S₁ и S₂ в моменты времени t_k, и , будут равны

,

.

Случайные события S₁ и S₂ представляют полную группу событий и поэтому

.

Вероятности появления событий и легко вычисляются, если заданы переходные вероятности и начальные вероятности и . Предположим, что , а . Переходные вероятности равны: , , , . Результаты расчетов вероятностей и приведены в таблице 1.5.1.

Таблица 1.5.1

	0	1	2	3	4	5
	1	0,5	0,55	0,545	0,5454	0,54545
	0	0,5	0,45	0,455	0,4546	0,45455

Изменим начальные вероятности на противоположные и снова подсчитаем вероятности и . Результаты приведены в таблице 1.5.2.

Таблица 1.5.2

	0	1	2	3	4	5
	0	0,6	0,54	0,546	0,5454	0,54546
	1	0,4	0,46	0,454	0,4546	0,45454

При вероятности и не зависят от номера , и в этом случае можно считать, что и . В результате получим формулы для оценки и при значениях

,

.

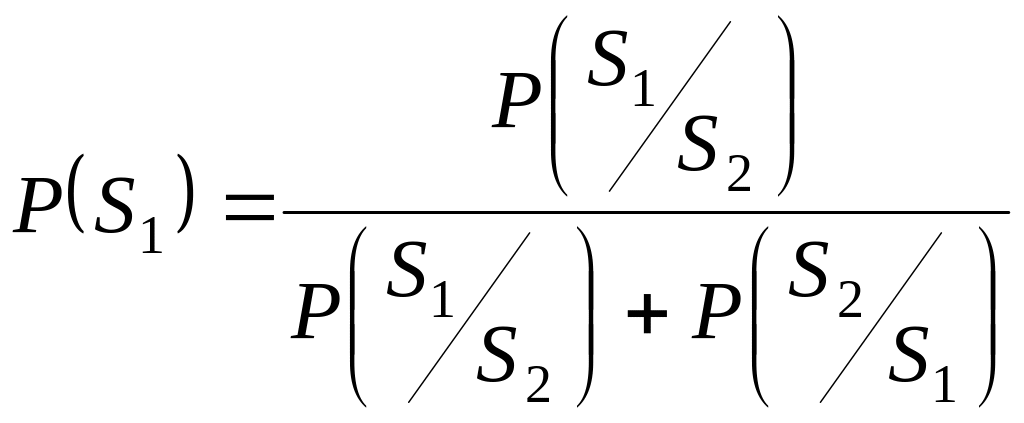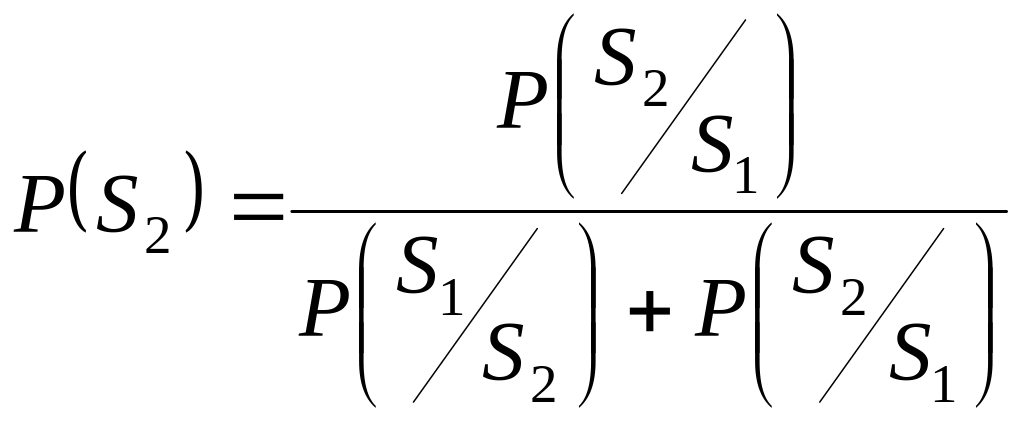Коэффициент корреляции

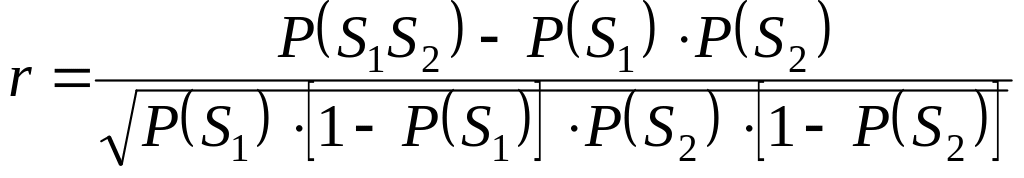
рассмотренной последовательности Маркова равен

.

Таким же образом можно описывать процессы, состоящие из трех и более событий, например, и т.д. Для их описания должны быть заданы начальные вероятности , , и вероятности перехода из состояния S₁ в состояния S₂, S₃ и т.д. Их можно записать в виде матрицы

.

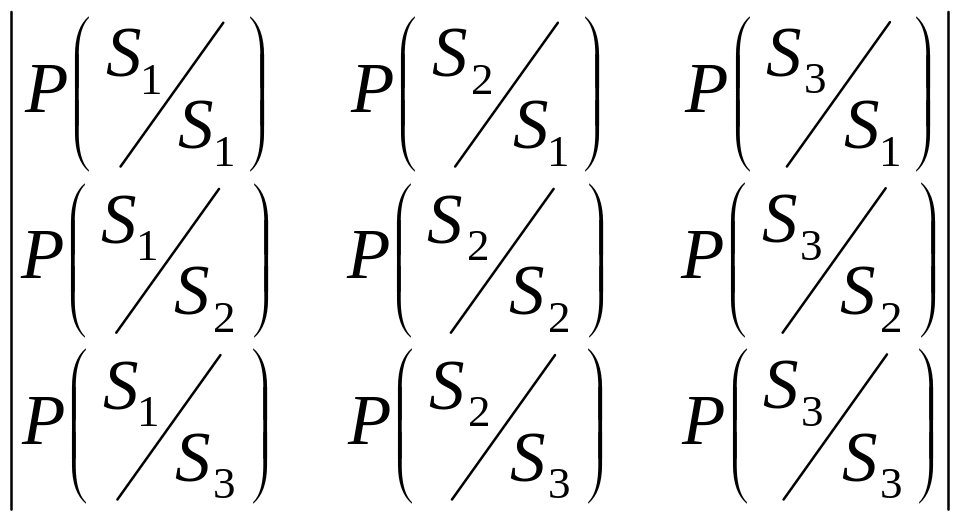Разностные уравнения, описывающие вероятности состояний S₁, S₂ и S₃, таковы

,

,

,

где , , .

1.6. Задачи для самостоятельного решения

Задача 1.6.1 В урне находится n₁ белых и n₂ черных шаров. Из урны вынимают один шар, и он оказывается белым. После этого вынимают еще один шар. Определить:

1) вероятность того, что первый вынутый из урны шар будет или белым или черным ;

2) определить условные вероятности того, что второй шар будет или белым , или черным ;

3) определить вероятность того, что второй вынутый шар будет белым, если бы первый шар оказался черным .

Задача 1.6.2 В урне находится n₁ белых и n₂ черных шаров. Из урны вынимают один шар и, не глядя, откладывают в сторону. После этого вынимают еще один шар. Определить вероятность того, что этот шар будет черным.

Задача 1.6.3 В урне находится n₁ белых и n₂ черных шаров. Из урны вынимают один шар и, не глядя, откладывают в сторону. После этого вынимают снова один шар, и он оказывается белым. Определить вероятность того, что отложенный шар будет белым.

Задача 1.6.4 В двух урнах находятся белые и черные шары, в первой их n₁ и n₂, во второй – m₁ и m₂. Выбирается наугад одна из урн и из нее вынимается один шар, который оказывается белым. Определить вероятность того, что следующий шар, который будет выниматься из этой урны, будет черным.

Задача 1.6.5 Прибор состоит из двух узлов, вероятности безопасной работы которых равны P₁ и P₂. После проведения испытаний оказалось, что прибор вышел из строя, причинами которого могут быть либо первый узел, либо второй узел, либо и первый, и второй совместно. Определить ожидаемую вероятность выхода прибора из строя до проведения испытаний и вероятности причин после испытаний.

Задача 1.6.6 Вероятность изготовления дефектных изделий в цехе равна P. Изделия контролируются в цехе тремя контроллерами и в ОТК завода одним опытным контроллером. Контроллеры характеризуются следующими показателями:

1) вероятностями пропуска бракованных изделий;

2) вероятностями перебраковки изделий в норме (ложный брак).

Эти вероятности равны:

1) контроллеров цеха P_Б1, P_Б2, P_Б3 и P_Л1, P_Л2, P_Л3;

2) контроллера ОТК P_Б0, P_Л0.

Определить вероятности пропуска бракованных изделий и перебраковки изделий в норме.

Задача 1.6.7 Блочные кодовые комбинации с одинаковым весом содержат одно и то же число единиц (вес кода). Помехи в линиях связи искажают символы кода (ноль преобразуется в единицу, а единица преобразуется в ноль). Если в принятой кодовой комбинации изменяется вес, то это означает, что она искажена помехами. Следовательно, такие кодовые комбинации могут быть обнаружены. Определить вероятность обнаружения искаженного семизначного кода с весом , если вероятность искажения помехами одного символа равна .

Задача 1.6.8 Коэффициент корреляции марковской последовательности символов S₁ и S₂ зависит от номера символов ( ). Записать формулу для и исследовать эту зависимость для трех вариантов начальных условий:

1) , ; 2) , ; 3) , ;

если переходные вероятности равны , .