
- •Сопротивление материалов
- •Введение
- •Схемы к задаче 1а
- •Схемы к задаче 1б
- •Контрольные вопросы к защите задач 1а и 1б
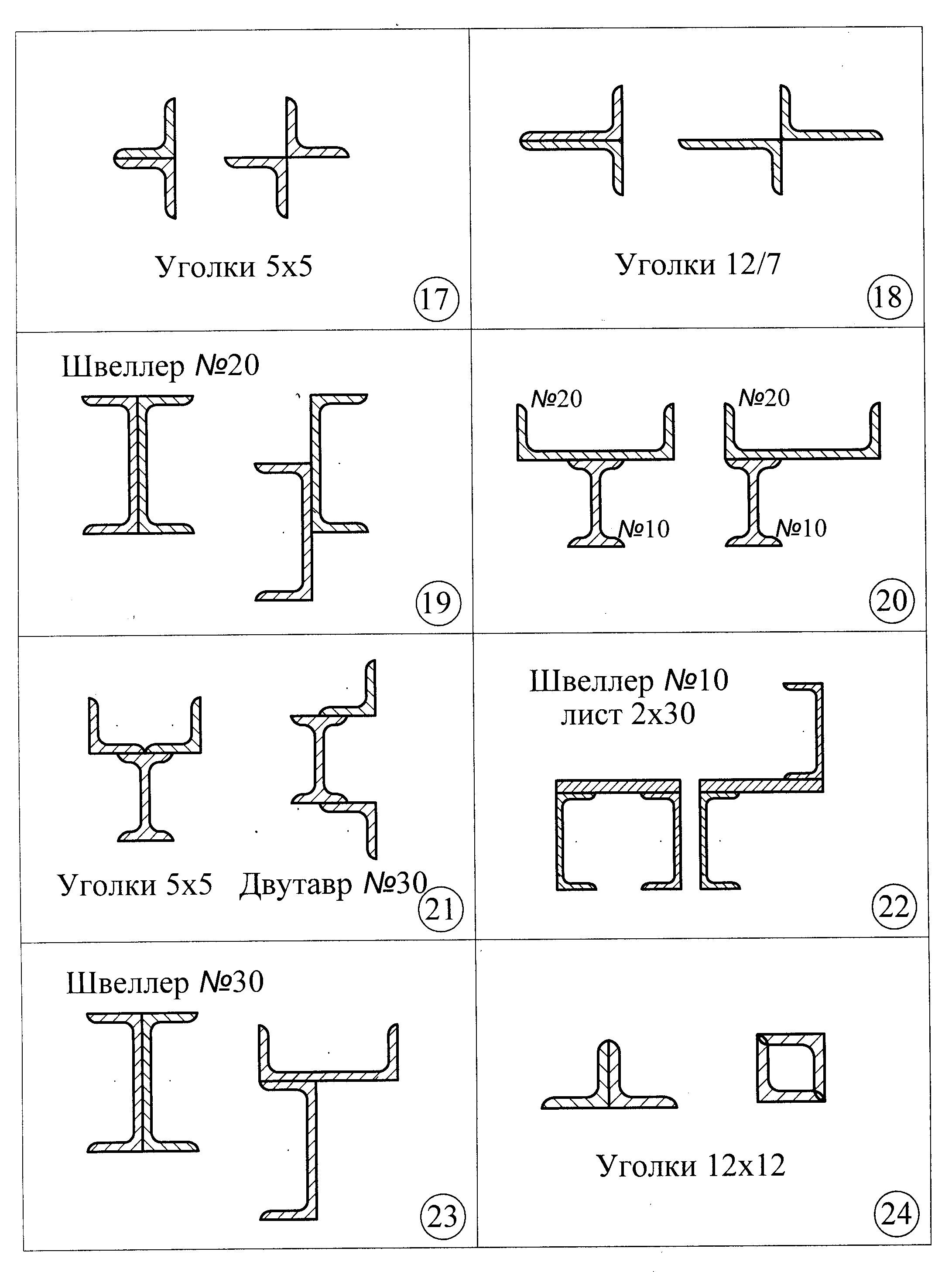
- •Схемы к задаче 2а
- •Схемы к задаче 2б
- •Контрольные вопросы к защите задач 2а, 2б и 2в
- •Схемы к задаче 3
- •Контрольные вопросы к защите задач 3а, 3б, 3в и 3г
- •Контрольные вопросы к защите задач 4
Схемы к задаче 2а
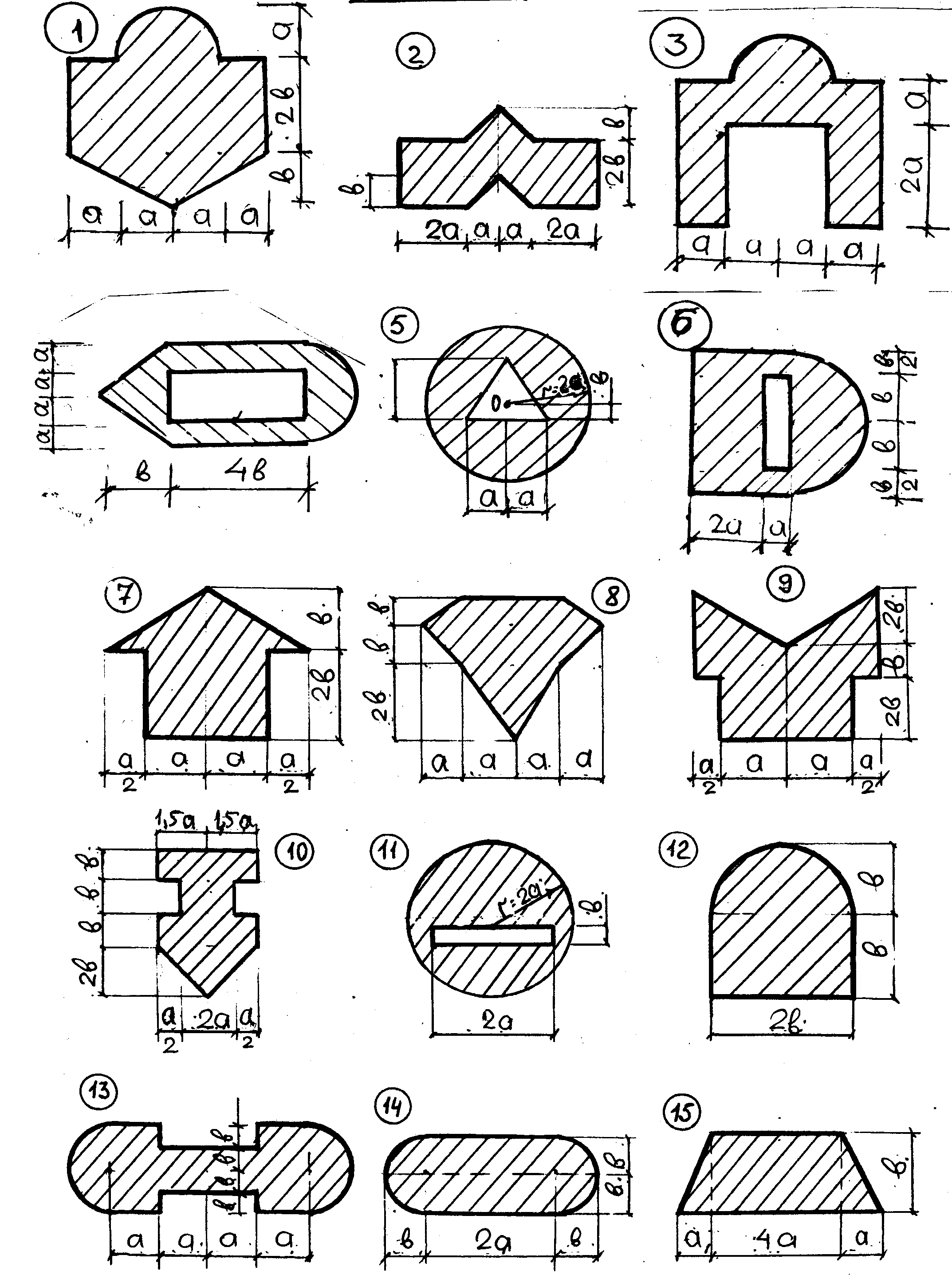
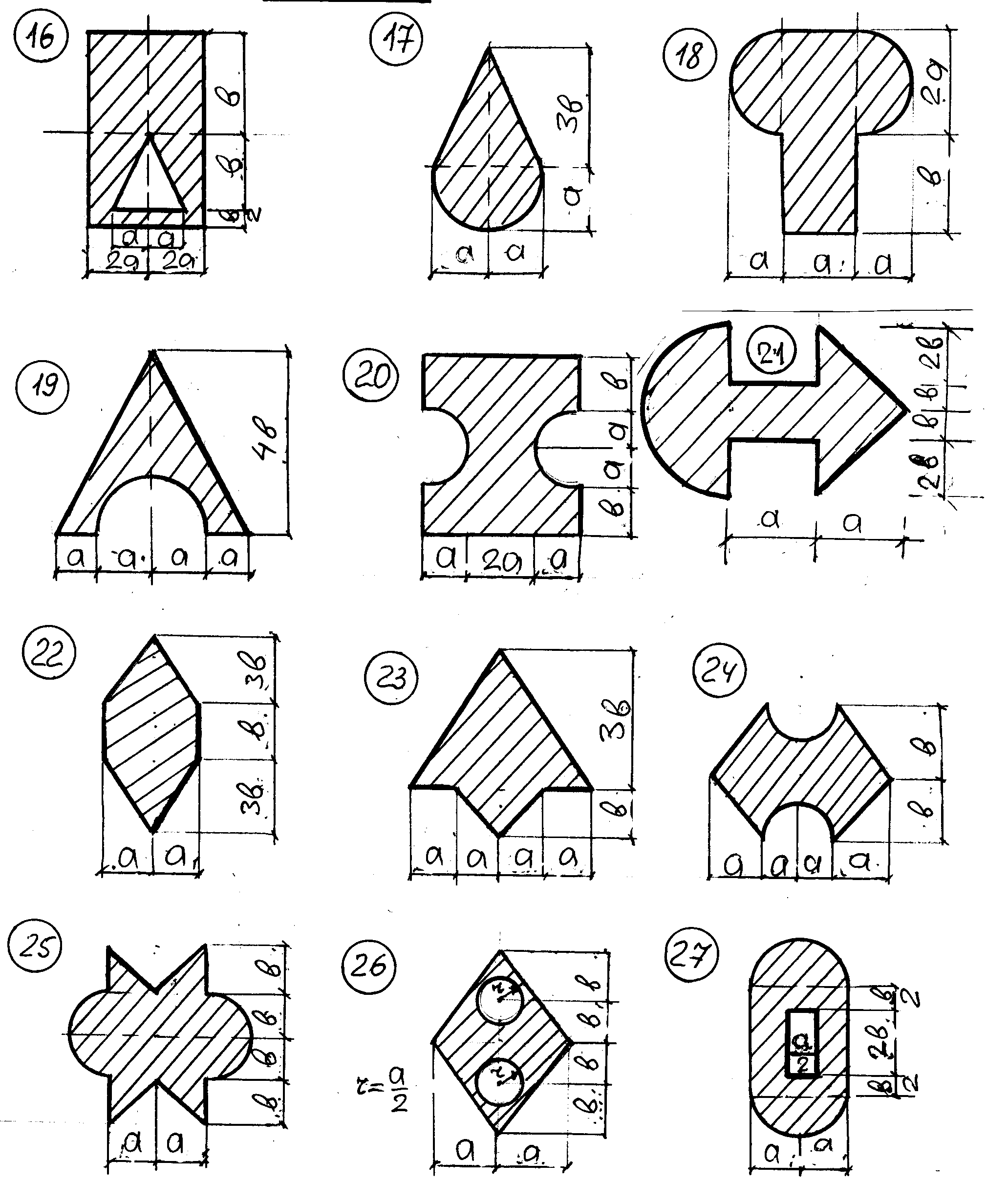
Схемы к задаче 2б
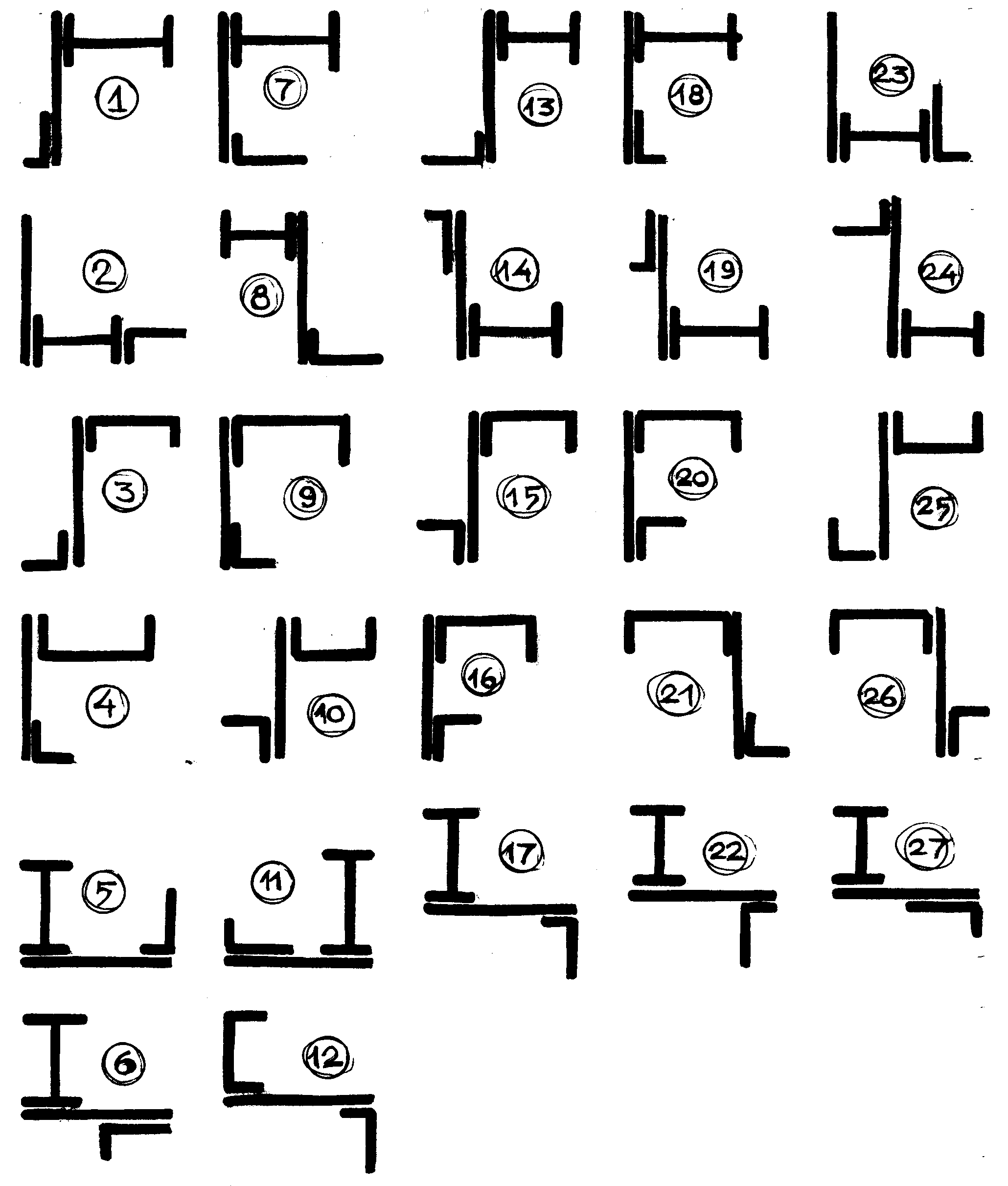
Задача 2в. Для каждой пары сечений, имеющих одинаковые площади
Требуется:
Найти и сравнить положения главных центральных осей.
Найти и сравнить величины главных центральных моментов инерции.

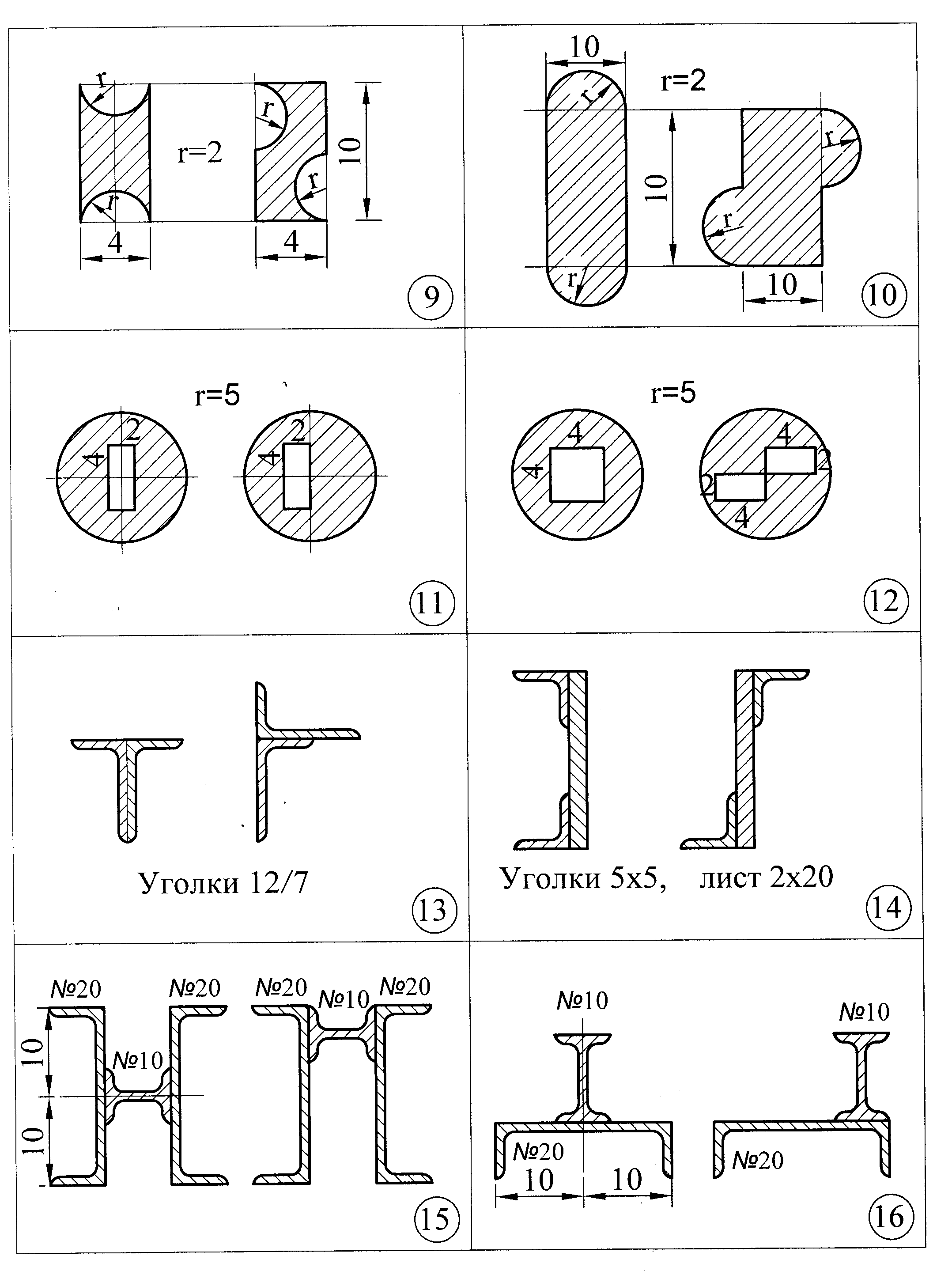
Контрольные вопросы к защите задач 2а, 2б и 2в
Статический момент, моменты инерции, момент сопротивления: их определения, размерности, знаки.
Чему равен статический момент сечения относительно центральной оси?
В каких случаях и какие геометрические характеристики обращаются в нуль?
Какие моменты инерции всегда положительны?
Как определить координаты центра тяжести сложного сечения?
Приведите формулы моментов инерции и моментов сопротивления для простых сечений (прямоугольник, круг, треугольник).
Как изменяется центробежный момент инерции при повороте осей на 90˚?
Какие оси называются главными центральными? Какими свойствами они обладают?
В каких случаях можно без вычислений установить положение главных осей?
Почему ось симметрии является всегда одной из главных центральных осей инерции?
В чем состоит закон суммы осевых моментов инерции?
Как вычисляется момент сопротивления сечения?
Как вычисляется радиус инерции?
Внимание! Подробные методические указания и примеры решения задач 2а, 2б и 2в содержатся в пособии [2], где они обозначены как «Задача 1», «Задача 2», «Задача 3», «Задача 4», «Задача 5» и «Задача 6» (все эти примеры размещены в разделе II пособия).
Задача 3а. Изгиб балки–консоли
Для каждой из двух схем требуется:
Найти опорные реакции построить эпюры изгибающих моментов и поперечных сил.
Подобрать сечения заданной формы:
– для балки № 1 – прямоугольное с заданным соотношением h/b,
– для балки № 1 – круглое.
Материал обоих балок: древесина с [σ] = 15 МПа, [τ] = 3 МПа.
Задача 3б. Изгиб балки на двух опорах
Для схемы № 3 требуется:
1. Найти опорные реакции и построить эпюры изгибающих моментов и поперечных сил.
2. Подобрать сечения заданной формы с таким же соотношением h/b.

Материал балки: чугун с [σ]раст.= 30 МПа, [σ]сжат.= 120 МПа, [τ] = 15 МПа.
Задача 3в. Изгиб балки с консолью
Для схемы № 4 требуется:
1. Найти опорные реакции и построить эпюры изгибающих моментов и поперечных сил.
2. Подобрать сечения в двух вариантах:

– вариант 1 – круглая труба с заданным соотношением внутреннего диаметра и внешнего d/D;

– вариант 2 – прямоугольной трубы с заданными соотношениями h/b и t/b/
Сравнить варианты по расходу материала.
Примечание: материал балки–сталь с [σ] = 160 МПа, [τ] = 80 МПа.
Задача 3г. Для балки с двумя консолями требуется:
Найти опорные реакции и построить эпюры изгибающих моментов и поперечных сил.
Подобрать двутавровое сечение.
Вычислить прогибы на конце каждой консоли и в середине пролета. По найденным величинам построить изогнутую ось балки и выполнить проверку жесткости, если допускается величина прогиба [y] = 1/200l, где l – длина прогиба балки.
УКАЗАНИЯ для задач 3а, 3б, 3в, 3г.
«Подбор сечения» балки означает:
а) определение размеров из условия прочности по нормальным напряжениям
![]() ,
а затем
,
а затем
б) проверку прочности по касательным напряжениям
![]() .
.
После подбора сечения постройте эпюры нормальных и касательных напряжений в опасных сечениях балки:
– эпюру σ в сечении, где возникают |max M|,
– эпюру τ в сечении, где возникают |max Q|.
Исходные данные:
Группа |
F, кН |
q, кН/м |
М, кНм |
Длина уча- стка а, м |
h/b |
d/D |
t/h |
ФЕК |
40 |
10 |
80 |
1,4 |
1,5 |
0,9 |
0,1 |
ФЕПО |
50 |
20 |
100 |
1,2 |
2,5 |
0,8 |
0,2 |
Резерв |
20 |
10 |
50 |
2 |
2 |
0,9 |
0,1 |
Модули упругости : – стали Е=2·1011 Па,
– чугуна Е=1,2·1011 Па,
– древесины Е=1·1010 Па.
