4. Моделі оптимізації портфеля.

Мета оптимізації портфеля цінних паперів – формування такого портфеля, який би відповідав вимогам підприємства як по прибутковості, так і по ризиках. Вона досягається шляхом збільшення кількості цінних паперів в портфелі.

Задача оптимізації формулюється наступним чином. Нехай доходність портфеля з N цінних паперів Rp та його показник ризику σp (сігма) визначаються наступними функціями:

Rp = (Wi, σi, ri; і = 1…N);

σр = (Wi, σi, ri; і = 1…N),

де Wi – питома вага цінного паперу в портфелі у відсотках, σi – характеристика ризику даного цінного паперу (часто – середнє квадратичне відхилення доходності цінного паперу), ri – доходність цінного паперу.

При побудові моделі слід враховувати природні обмеження:

сума часток всіх цінних паперів Wi становить 100%, кількість цінних паперів не може бути від’ємним значенням.

При вирішенні задачі введемо критеріальні обмеження.

І варіант – задається певна максимально допустима величина ризику σreg. Тоді задача оптимізації зводиться до вибору такої структури портфеля, при якій ризик портфеля не перевищує заданого значення, а його доходність є максимальною.

Rp max;

σр ≤σreg;

Wi ≥ 0;

Σ Wi = 1.

ІІ варіант – задається певна мінімально прийнятна величина прибутковості Rreg. В цьому випадку задача оптимізації зводиться до вибору структури такого портфеля, доходність якого вища або дорівнює заданому значенню, а ризик мінімальний:

Rp ≥ Rreg.;

σр min;

Wi ≥ 0;

Σ Wi = 1.

Модель «Квазі-Шарп» здатна працювати в умовах нашого фондового ринку та по деяких характеристиках подібна до моделі Шарпа.

Основні припущення моделі полягають в наступному:

- в якості прибутковості цінного паперу приймається математичне очікування прибутковості;

- під одиничним портфелем цінних паперів розглядається портфель, який складається з усіх цінних паперів, що розглядаються, та взяті в рівній пропорції;

- взаємозв’язок прибутковості цінного паперу та прибутковості одиничного портфеля описується лінійною функцією;

- під ризиком цінного паперу розуміється ступінь прибутковості цінного паперу від змін прибутковості одиничного портфеля;

- вважається, що данні минулих періодів, які використовуються при розрахунку прибутковості і ризику, відображають в повній мірі значення прибутковості.

Згідно моделі «Квазі-Шарп» прибутковість цінного паперу пов’язується з прибутковістю одиничного портфеля функцією лінійної регресії:

__ __

Ri = Ri + βi (Rsp – Rsp),

де Ri – прибутковість цінного паперу;

βi – коефіцієнт регресії;

__

Ri – середня прибутковість цінного паперу за минулі періоди;

__

Rsp – середня прибутковість одиничного портфеля за минулі періоди.

Коефіцієнт β характеризує ступінь залежності прибутковості цінного паперу від прибутковості одиничного портфеля, і чим він вищий, тим сильніша залежність коливань прибутковості цінного паперу від коливань прибутковості одиничного портфеля. Коефіцієнт β називають β-ризиком.

Рівняння, яке встановлює зв’язок між ризиком акції, що вимірюється β, і прибутковістю акції, називається рівнянням ринку цінних паперів – SLM:

ki = kRF + (kM – kRF ) х βi,

де ki – необхідна прибутковість акції, kRF - безризикова прибутковість, kM – необхідна дохідність портфеля.

Лінія ринку цінних паперів має наступний вигляд:

k,%

kRF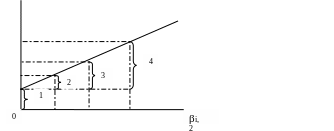

1 – без ризикова прибутковість, 2 – премія за ризик володіння володіння відносно безпечною акцією, 3 – премія за ринковий ризик, 4 – премія за ризик володіння відносно ризиковою акцією.

Згідно моделі «Квазі-Шарп» прибутковість портфеля цінних паперів – це середньозважена прибутковостей цінних паперів, що входять до нього.

N N

Rр = ∑ (Ri х Wі) + (Rsp - Rsp ) х ∑ (βi х Wі),

і=1 і=1

де Rsp – очікувана прибутковість одиничного портфеля.

Ризик портфеля цінних паперів визначається за формулою:

N N

σр = ∑ √ (βi х Wі)² х σsp² + ∑ (σεі² х Wі²) ,

і=1 і=1

де σsp – очікувана прибутковість одиничного портфеля, σεі – кінцевий ризик і-того цінного паперу.

З використанням моделі пряма задача набуває вигляду:

N N

∑ (Ri х Wі) + (Rsp - Rsp ) х ∑ (βi х Wі) → max;

і=1 і=1

N N

√∑ (βi х Wі)² х σsp² + ∑ (σεі² х Wі²) ≤σreg;

і=1 і=1

Wi ≥ 0;

∑ Wi = 1.

Відповідного вигляду набуває обернена задача.

Питання для самоконтролю та самопідготовки

1. Дайте визначення інвестиціям.

2. Які об’єкти інвестиційних вкладень Ви знаєте?

3. Що розуміється під фінансовими інвестиціями?

4. Які основні цілі здійснення фінансових інвестицій?

5. Які основні підходи до оцінювання інвестицій?

6. Схарактеризуйте методи оцінювання фінансових інвестицій: дисконтування Cash-flow, ефективної ставки відсотку, визначення внутрішньої норми прибутковості.

7. Для чого розраховується показник дюрація?

8. Перелічити заходи щодо управління портфелем цінних паперів.

9. Що має на меті корпорація при формуванні портфеля цінних паперів?

10. Які способи управління портфелем цінних паперів Ви знаєте?

11. Які критерії враховуються при оптимізації портфеля цінних паперів?

12. Дайте коротку характеристику моделям оптимізації портфеля цінних паперів (Марковиця, Шарпа, Квазі-Шарпа).

Література:

- Терещенко О.О. Фінансова діяльність суб’єктів господарювання. – К., 2003. – С.333-339.

- Савчук В.П. Практическая энциклопедия. Финансовый менеджмент. – К.: Издательский дом «Максимум», 2005. – С. 792-803.

- Брегхем Ю. Фінансовий менеджмент.т.1. С.-П. – 1998. – с. 79-80.

Лекція 15. Фінансові аспекти реорганізації корпорації

1. Загальні поняття та передумови реорганізації.

2. Укрупнення корпорації.

3. Реорганізація корпорації, спрямована на її розукрупнення.

4. Перетворення.