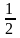- •Розв’язати систему трьох лінійних рівнянь методом Гаусса:
- •4. Знайти загальний розв'язок диференціального рівняння
- •Розв’язати систему трьох лінійних рівнянь за допомогою
- •Знайти загальний розв'язок диференціального рівняння
- •4. Знайти похідні функцій
- •Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •2. Знайдіть а*(в-е), де е –одинична матриця третього порядку в
- •4. Знайти похідні функцій:
- •Розв’язати систему трьох лінійних рівнянь за допомогою
- •1. Розв’язати систему трьох лінійних рівнянь за допомогою
- •4. Знайти похідні функцій
- •4. Знайти похідні функцій:
- •1.Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •Розв’язати систему трьох лінійних рівнянь за допомогою
- •Визначити, яка крива другого порядку задана рівнянням
- •Розв’язати систему трьох лінійних рівнянь за допомогою
- •1 .Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •2.Знайти похідні функцій:
- •1.Розв’язати систему трьох лінійних рівнянь за допомогою
- •2.Знайти похідні функцій:
- •1.Розв’язати систему трьох лінійних рівнянь за допомогою
- •1 .Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •Знайти загальний розв'язок диференціального рівняння
- •Визначити, яка крива другого порядку задана рівнянням
- •Розв’язати систему трьох лінійних рівнянь за допомогою
- •Знайдіть а*(в-е), де е –одинична матриця третього порядку в
- •Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •Знайти проміжки зростання, спадання і екстремум функції .
- •Міністерство освіти і науки, молоді та спорту України
- •2 Курс 4 семестр
- •Перелік питань до іспиту
- •4 Семестр 2 курсу
- •1.Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •3. Знайти загальний розв'язок диференціального рівняння
- •4. Знайти частинні похідні першого порядку функції двох
- •1.Розв’язати систему трьох лінійних рівнянь методом Гаусса:
- •4. Знайти загальний розв'язок диференціального рівняння
- •Розв’язати систему трьох лінійних рівнянь за допомогою
- •Знайти загальний розв'язок диференціального рівняння
- •4. Знайти похідні функцій
- •1.Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •2. Знайдіть а*(в-е), де е –одинична матриця третього порядку в
- •4. Знайти похідні функцій:
- •Розв’язати систему трьох лінійних рівнянь за допомогою
- •1. Розв’язати систему трьох лінійних рівнянь за допомогою
- •4. Знайти похідні функцій
- •4. Знайти похідні функцій:
- •1.Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •Розв’язати систему трьох лінійних рівнянь за допомогою
- •4.Визначити, яка крива другого порядку задана рівнянням
- •1.Розв’язати систему трьох лінійних рівнянь за допомогою
- •1 .Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •2.Знайти похідні функцій:
- •1.Розв’язати систему трьох лінійних рівнянь за допомогою
- •2.Знайти похідні функцій:
- •1.Розв’язати систему трьох лінійних рівнянь за допомогою
- •1 .Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •Знайти загальний розв'язок диференціального рівняння
- •Визначити, яка крива другого порядку задана рівнянням
- •Розв’язати систему трьох лінійних рівнянь за допомогою
- •Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •Розв’язати систему трьох лінійних рівнянь методом Гаусса
- •Міністерство освіти і науки, молоді та спорту України
- •2 Курс 4 семестр
Розв’язати систему трьох лінійних рівнянь методом Гаусса

Знайти повний диференціал функції двох змінних
![]()
Знайти координати центра і радіус кола
![]()
Знайдіть А2 +(В-Е), де Е – одинична матриця третього порядку
Затверджено на засіданні комісії математики та фізико-хімічних дисциплін
Протокол №____ від „____” ________________ 2012року
Голова циклової комісії ____________________О.М Пугачова
Екзаменатор _________ О.Б.Мачкаріна
Форма № Н-5.05
Міністерство освіти і науки, молоді та спорту України
Державний вищий навчальний заклад
«Донецький технікум промислової автоматики»
Освітньо-кваліфікаційний рівень молодшій спеціаліст
Напрям підготовки 030504 «Економіка підприємства»
Спеціальність 5.03050401 «Економіка підприємства»
Семестр 4
Навчальна дисципліна Вища математика
Екзаменаційний білет № 30
Розв’язати систему трьох лінійних рівнянь за допомогою правила Крамера

Знайти проміжки зростання, спадання і екстремум функції .
Знайти частинний розв'язок диференціальне рівняння, який задовольняє початковим умовам:
, якщо у=2 при х=1
Скласти рівняння еліпса з фокусами на осі ОХ, якщо більша вісь дорівнює 14, а ексцентриситет е=2/3.Записати координати вершин еліпса та його фокусів.
Затверджено на засіданні комісії математики та фізико-хімічних дисциплін
Протокол №____ від „____” ________________ 2012року
Голова циклової комісії ____________________О.М Пугачова
Екзаменатор _________ О.Б.Мачкаріна
Міністерство освіти і науки, молоді та спорту України
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
«ДОНЕЦЬКИЙ ТЕХНІКУМ ПРОМИСЛОВОЇ АВТОМАТИКИ»
Розглянуто і схвалено Затверджую:
на засіданні комісії математики Директор ДВНЗ «ДТПА»
та фізико-хімічних дисциплін
Протокол № ___ від ____ 2012р. ___________О.І.Максецький
Голова комісії
___________ О.М.Пугачова «____»____________ 2012р.
ЕКЗАМЕНАЦІЙНІ БІЛЕТИ
з дисципліни ВИЩА МАТЕМАТИКА
2 Курс 4 семестр
для студентів
спеціальності 5.03050401 «Економіка підприємства»
напряму 030504 «Економіка підприємства»
Склав викладач О.Б. Мачкаріна
Перелік питань до іспиту
4 Семестр 2 курсу
спеціальності 5.03050401 «Економіка підприємства»
напряму 030504 «Економіка підприємства»
1. Основні поняття та означення матричного числення. Види матриць. Дії над матрицями.
2. Визначники 2 порядку, їх обчислення, властивості.
3. Визначники 3 порядку, методи обчислення ( правило трикутника та розкладання визначника за елементами першої строки – теорема Лапласа). Властивості визначників 3 порядку.
4. Поняття оберненої матриці. Алгоритм знаходження оберненої матриці.
5. Розв’язування систем трьох лінійних рівнянь з трьома невідомими за допомогою правила Крамера
6. Розв’язування систем трьох лінійних рівнянь з трьома невідомими методом Гаусса.
7. Розв’язування систем трьох лінійних рівнянь з трьома невідомими матричним способом.
8. Загальне рівняння прямої на площині. Види неповних рівнянь та розміщення прямих на координатній площині. Рівняння прямої, яка проходить через дві задані точки. Рівняння прямої у відрізках. Рівняння прямої з кутовим коефіцієнтом.
9. Умови паралельності та перпендикулярності прямих. Точки перетину прямих. Кут між прямими.
10. Коло і еліпс. Канонічне рівняння еліпса.
11. Гіпербола. Канонічне рівняння гіперболи.
12. Парабола. Канонічне рівняння гіперболи.
13. Границя функції у точці. Теореми про границі .
14. Границя функції на нескінченості. Перша і друга важливі границі. Розкриття невизначеностей.
15. Неперервність функції у точці. Властивості неперервних функцій. Дослідження на неперервність.
16. Означення похідної. Формули диференціювання. Техніка диференціювання функцій.
17. Складна функція. Техніка диференціювання складних функцій.
18. Диференціал функції однієї змінної та його застосування до наближених обчислень.
19. Основні теореми диференціального числення.
20. Умови монотонності та екстремуму функції. Умови вгнутості та опуклості функції. Точки перегину.
21. Найбільше та найменьше значення функції на відрізку. Оптимізаційні задачі.
22. Дослідження функції за допомогою похідної та побудова графіка функції.
23. Поняття функції багатьох змінних. Задачі, які приводять до поняття функції двох змінних. Частинні похідні функції двох змінних.
24. Повний диференціал функції двох змінних і його застосування до обчислення наближеного значення приросту функції.
25. Екстремум функції двох змінних. Алгоритм знаходження екстремуму функції двох змінних. Умовний екстремум функції двох змінних.
26. Означення первісної, означення невизначеного інтеграла, властивості та таблиця інтегралів. Інтегрування виразів методом безпосереднього інтегрування.
27. Інтегрування виразів: метод інтегрування заміни змінної; метод інтегрування частинами.
28. Задача про обчислення площі криволінійної трапеції. Визначений інтеграл та його властивості. Формула Ньютона-Лейбниця.
29.Обчислення визначених інтегралів методами: безпосереднього інтегрування, заміни змінної, частинами.
30. Застосування визначеного інтеграла для розв'язання прикладних задач.
31. Поняття про диференціального рiвняння, його загальний i частинний розв’язок. Задача Коши. Диференціальні рiвняння першого порядку з вiдокремлюваними змiнними.
32. Лінійні диференційні рівняння першого порядку.
Знайти невизначений інтеграл:
а)
![]() б)
б)


Индивидуальные задания для самостоятельной работы.
Ответы
1. xdy = ydx, y(2) = 6. |
1. y = 3x. |
2. 3y2dy = x2dx, y(3) = 1. |
2. y =
|
3. ’ = xe-y, y(1) = 0. |
3. y =
ln |
4.
|
4. y = x = 5et – 2 |
5.
–
|
5. y = 5x |
6. (x – 1)dy = (y + 1)dx, y(2) = 3 |
6. y = 4x – 5 |
7. – 2y = 1, y(0) = 12 |
7. y =
e2x
–
|
8. – y = x; y(1) = 1 |
8. y = 2x3 – x2 |
9. 2 – y = ex, y(0) = 5 |
9. y = ex + 4ex/2 |
10. – 2xy = e , y(2) = 0 |
10. y = (x – 2)e |
Форма № Н-5.05
Міністерство освіти і науки, молоді та спорту України
Державний вищий навчальний заклад
«Донецький технікум промислової автоматики»
Освітньо-кваліфікаційний рівень молодшій спеціаліст
Напрям підготовки 030509 «Облік і аудит»
Спеціальність 5.03050901 «Бухгалтерський облік»
Семестр 4
Навчальна дисципліна Вища математика
Екзаменаційний білет № 1
Розв’язати систему трьох лінійних рівнянь за допомогою
правила Крамера
.
Знайти загальний розв'язок диференціального рівняння першого порядку:
Знайти похідні функцій:
а) б)
4. Визначити, яка крива другого порядку задана рівнянням
.
Виконати дослідження цієї кривої.
Затверджено на засіданні комісії математики та фізико-хімічних дисциплін
Протокол №____ від „____” ________________ 2012року
Голова циклової комісії ____________________О.М Пугачова
Екзаменатор _________ О.Б.Мачкаріна
Форма № Н-5.05
Міністерство освіти і науки, молоді та спорту України
Державний вищий навчальний заклад
«Донецький технікум промислової автоматики»
Освітньо-кваліфікаційний рівень молодшій спеціаліст
Напрям підготовки 030509 «Облік і аудит»
Спеціальність 5.03050901 «Бухгалтерський облік»
Семестр 4
Навчальна дисципліна Вища математика
Екзаменаційний білет № 2


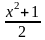
 = 2 + x,
x(0)
= 3
= 2 + x,
x(0)
= 3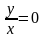 ;
y(1) = 5.
;
y(1) = 5.