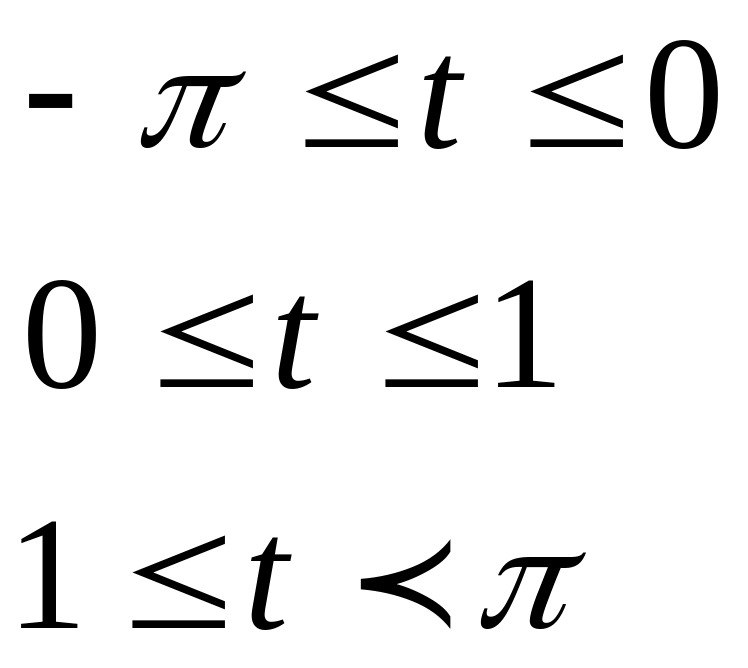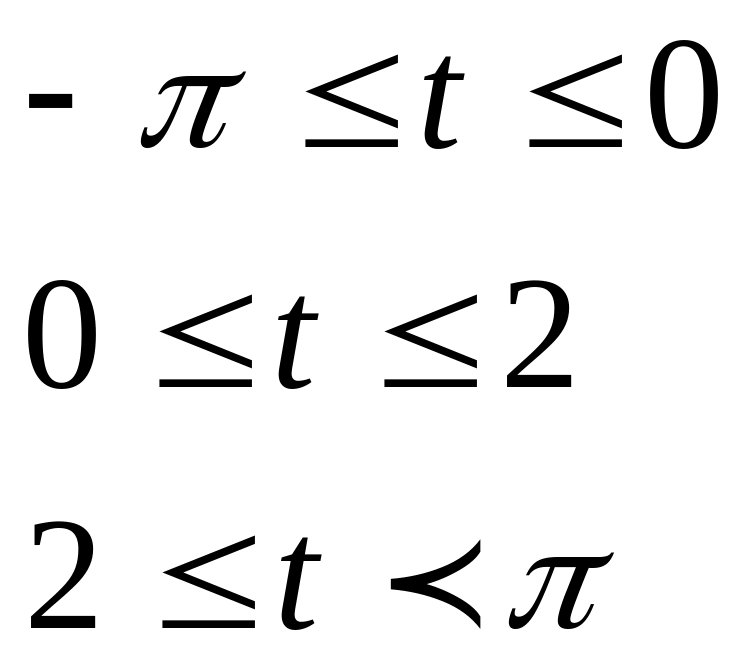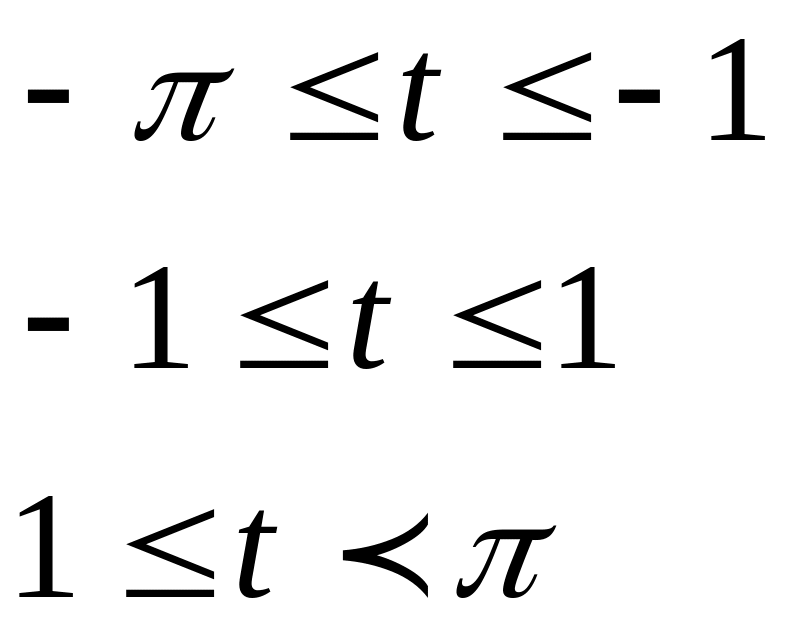Лабораторная работа №2 разложение функции в ряд фурье

Цель работы: ознакомление студентов с одним из наиболее важных преобразований, используемых в обработке геофизических данных. На основе выполнения этой работы студент может наглядно убедиться в улучшении качества функции, раскладываемой в ряд Фурье.

2.1 Вопросы теории и методики

Любую временную функцию практически любой формы, если эта функция удовлетворяет условиям Дирихле, можно представить в виде ряда Фурье:

, (2.1)

где - коэффициенты Фурье.

Основное свойство ряда Фурье заключается в том, что любую периодическую функцию можно представить в виде набора гармоник с различными частотами, которые будут кратны основной частоте . Чем больше будет количество гармоник, тем лучше будет аппроксимация временной функции.

Процесс вычисления коэффициентов Фурье называется гармоническим анализом. Эти коэффициенты можно вычислить, используя следующие формулы:

, (2.2)

, (2.3)

, (2.4)

2.2 Задание

2.2.1 Построить график функции (таблица 2.1) в масштабе в 1 см-0.5 единиц

2.2.2 Просчитать коэффициенты Фурье с помощью формул (2.2-2.4), для заданного количества членов и . Если коэффициенты не равны 0, то можно в расчетах использовать по и членов.

2.2.3 Разложить коэффициенты Фурье с помощью формулы (2.1)

2.2.4 Построить график функции с использованием полученного ряда для и членов. Вид временной функции, интервалы ее изменений во времени и числа и заданы в таблице 2.1

2.3 Содержание отчета

2.3.1 Описание теории разложения функции в ряд Фурье.

2.3.2 Методика разложения в ряд Фурье.

2.3.3 Вычисление Фурье коэффициентов, разложение заданной функции в ряд, вычисление по полученной формуле графика разложенной в ряд функции.

2.3.4 Графики, схемы, приложения.

2.4 Контрольные вопросы

2.4.1 Любую ли функцию можно разложить в ряд Фурье?

2.4.2 Что такое гармонический анализ?

2.4.3 Объяснить смысл разложения в ряд Фурье.

2.4.4 Сделать практический вывод по работе.

Таблица 2.1

Номер варианта	Вид функции
1		2	8
2		2	6
3		4	6
4		2	8
5		2	8
6		4	6

Продолжение таблицы 2.1

Номер варианта	Вид функции
7		2	6
8		2	8
9		2	8
10		2	6
11		2	6
12		2	8
13		2	8
14		2	6
15		2	8

Примечание: при построении графиков взять шаг