Введение

Геофизические методы служат для информационного обеспечения поисков и разведки полезных ископаемых. В настоящее время одним из главных направлений повышения эффективности геофизических работ является повсеместное использование цифровой регистрации и обработки данных геофизических методов. Поэтому всем бакалаврам-геофизикам необходима подготовка в области вычислительной техники. Такую минимальную подготовку призван обеспечить курс «Теоретические основы обработки геофизической информации». Курс посвящен изложению основ теории линейных цифровых процедур, используемых при регистрации и обработке данных. Данные методические указания помогут студентам в освоении теоретических основ физико-математических преобразований временных рядов и применении теории на практике геофизических работ.

Лабораторная работа №1 приближенное представление определенных интегралов в дискретной форме

Цель работы: Ознакомление с различными методами вычисления определенных интегралов. Результаты расчетов позволяют понять способы вычисления различных интегральных преобразований, которые используются при обработке геофизической информации.

1.1 Вопросы теории и методики

Получаемая с помощью аналоговой аппаратуры запись каждой сейсмической трассы представляет собой функцию времени и пространства или функцию непрерывного времени вида . Такой сигнал называется аналоговым. ЭВМ такое представление сигналов не понимает, поэтому каждую сейсмическую трассу представляют в виде набора цифр двоичного кода: 0 или 1. Двоичный код при оцифровке сейсмического сигнала используется потому, что им удобно моделировать электрические цепи, т.е. если электрический сигнал есть, то записывается 1, нет – 0. Такую процедуру называют дискретизацией сигнала. Дискретизация реализуется в 2 этапа: дискретизации по времени и дискретизации по уровню. Эта процедура является начальной и важной, так как правильно сделанная дискретизация сигнала исключает появление дополнительных помех и неточностей. В дальнейшем дискретный сигнал подвергается различным преобразованиям, которые имеют интегральный вид, а ЭВМ должна посчитать их в дискретном виде. Существуют специальные алгоритмы, которые направлены на решение данной задачи. Данная лабораторная работа знакомит со следующими методами дискретного вычисления определенных интегралов: формулы прямоугольников, трапеций и Симпсона.

1.1.1 Формула прямоугольников

Пусть на отрезке или задана непрерывная функция . Требуется представить определенный интеграл в дискретной форме.

Разделим отрезок точками на равных частей длиной (рисунок 1.1)

Значения функции в точках 0, ∆t, 2∆t,…N∆t соответственно , , ….. .

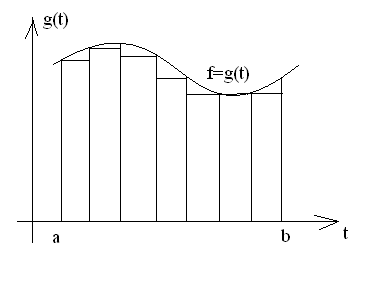
Рисунок 1.1 – Разделение заданной функции на прямоугольники

Из рисунка видно, что любую функцию можно представить в виде набора прямоугольников и площадь всей функции (а смысл интегрирования – это нахождение площади) можно найти, если вычислить площадь каждого прямоугольника в отдельности, а затем все площади сложить, т.е.

. (1.1)

Это и есть формула прямоугольников. Если функция положительная и возрастающая функция, то формула (1.1) выражает площадь ступенчатой фигуры, составленной из «входящих» прямоугольников. Если нет, то площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников.