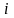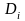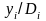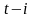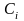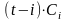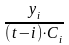- •3. Інтерполювання і екстрополювання функцій
- •3.1 Теоретичні відомості
- •2. Інтерполяційні формули Ньютона.
- •3. Апроксимація експериментальних даних методом найменших квадратів (мнк).
- •3.2 Приклади роз’язування завдань та завдання для самостійної і домашньої робіт Завдання 1.
- •Варіанти до завдання 1.
- •Приклад виконання завдання
- •Завдання 2
- •Варіанти до завдання 2
- •Завдання 3.
- •Варіанти до завдання 3.
- •Приклад виконання завдання
Приклад виконання завдання
1) |
2) |
||||
|
|
|
|
|
|
0,02 |
1,02316 |
|
0,115 |
8,65729 |
|
0,08 |
1,09590 |
|
0,120 |
8,29329 |
|
0,12 |
1,14725 |
|
0,125 |
7,95829 |
|
0,17 |
1,21483 |
|
0,130 |
7,64893 |
|
0,23 |
1,30120 |
|
0,135 |
7,36235 |
|
0,30 |
1,40976 |
|
0,140 |
7,09613 |
|
Обчислити
значення функції
|
|
Визначити
значення функції
|
|||
_____________________________________________________
1)
Скористаємося формулою
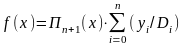 .
.
Обчислення наведено в таблиці:
|
Різниці |
|
|
|||||
0 |
0,102 |
–0,06 |
–0,10 |
–0,15 |
–0,21 |
–0,28 |
–0,539784·10-5 |
–189549,89 |
1 |
0,06 |
0,042 |
–0,04 |
–0,09 |
–0,15 |
–0,22 |
0,299376·10-6 |
3660614,0 |
2 |
0,10 |
0,04 |
0,002 |
–0,05 |
–0,11 |
–0,18 |
–0,792·10-8 |
–144854790,0 |
3 |
0,15 |
0,09 |
0,05 |
–0,048 |
–0,06 |
–0,13 |
–0,25272·10-6 |
–4807019,6 |
4 |
0,21 |
0,15 |
0,11 |
0,06 |
–0,108 |
–0,07 |
0,1571724·10-5 |
827880,72 |
5 |
0,28 |
0,22 |
0,18 |
0,13 |
0,07 |
–0,178 |
–0,17960342·10-4 |
–2531,9768 |
Отже,
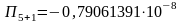 ,
,
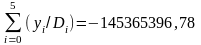 .
.
Тому,
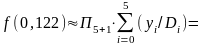
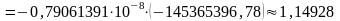 .
.
2) Для обчислень використовуємо формулу
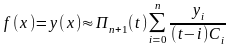 ,
,
де
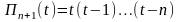 ;
;
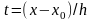 ;
;
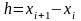 ;
;
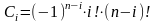 .
.
Тут
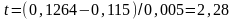 .
.
Обчислення розміщуємо в таблиці:
|
|
|
|
|
|
|
0 |
0,115 |
8,65729 |
2,28 |
–120 |
–273,6 |
–0,031642141 |
1 |
0,120 |
8,29329 |
1,28 |
24 |
30,72 |
0,26996386 |
2 |
0,125 |
7,95829 |
0,28 |
–12 |
–3,36 |
–2,3685386 |
3 |
0,130 |
7,64893 |
–0,72 |
12 |
–8,64 |
–0,88529282 |
4 |
0,135 |
7,36235 |
–1,72 |
–24 |
41,28 |
0,1783515 |
5 |
0,140 |
7,09613 |
–2,72 |
120 |
–326,4 |
–0,021740594 |
Отже,
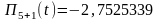 ;
;
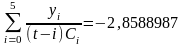 .
.
Тому,
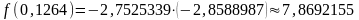 .
.

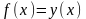 при
при
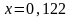 .
.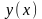 при
при
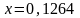 .
.