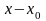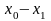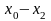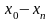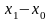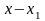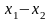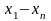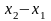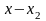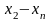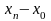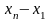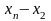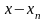3. Інтерполювання і екстрополювання функцій

3.1 Теоретичні відомості

1. Інтерполяційна формула Лагранжа:

.

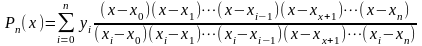При обчисленні коефіцієнтів Лагранжа різниці зручно розміщувати наступним чином:

Якщо позначити добуток елементів рядків через 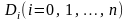, а добуток елементів головної діагоналі (підкреслені) – через 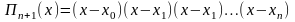, то одержимо формулу

.

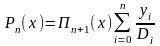У випадку рівновіддалених вузлів інтерполяційна формула Лагранжа приймає вигляд

,

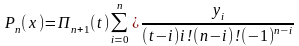де .

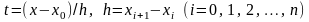Для оцінки похибки інтерполяційної формули Лагранжа можна використовувати співвідношення

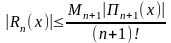, де .

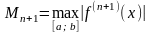2. Інтерполяційні формули Ньютона.

а) Перша інтерполяційна формула Ньютона:

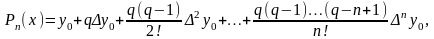
де 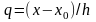, , 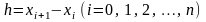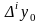- скінченна різниця 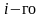порядку, причому .

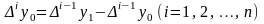При 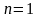, одержується формула лінійної інтерполяції

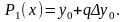
При 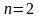, одержується формула квадратичної інтерполяції

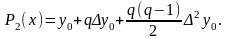
б) Друга інтерполяційна формула Ньютона:

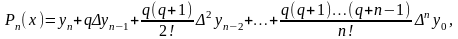
де .

в) Інтерполяційна формула Ньютона для нерівновіддалених значень аргумента:

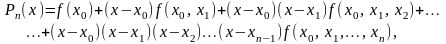
де 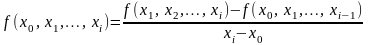- розділена різниця порядку.

3. Апроксимація експериментальних даних методом найменших квадратів (мнк).

Основою МНК є вимога мінімальності

суми квадратів

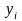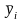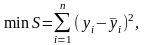відхилень фактичних значень (даних) від розрахункових , тобто де 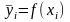- конкретне значення апроксимуючої функції для відповідних 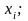або

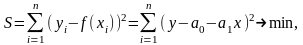
якщо 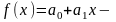лінійна апроксимуюча функція (або рівняння регресії).

При розгляді 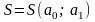, як функції двох параметрів,

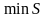
буде у точці, для якої 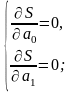- необхідна умова існування екстремуму, яка, у випадку лінійної функції, дає, так звану, систему нормальних рівнянь:

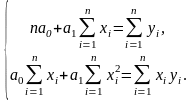
Розв’язавши цю систему, визначимо параметри 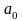, 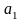лінійної функції – рівняння апроксимуючої залежності .

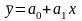Для деяких випадків, коли функція не лінійна, вона за допомогою аргумента-фактора зводиться до лінійної - це метод лінеаризації рівнянь апроксимуючої залежності.

До таких випадків відносять:

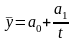1. Якщо : заміна аргументу 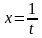зводить рівняння до виду

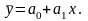
2. Якщо 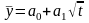: заміна 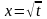; або якщо 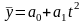: заміна 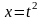зводить до виду .

3. Якщо , то прологарифмувавши рівняння одержимо

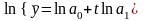і заміна змінних ,

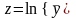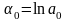
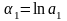дає

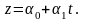
3. Якщо 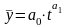, то аналогічно до випадку 3: 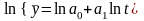, , , 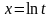і

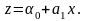
У інших випадках для апроксимуючої 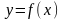функції складається відповідна система нормальних рівнянь, з якої і знаходять невідомі параметри (коефіцієнти), що визначають конкретне рівняння функції .

3.2 Приклади роз’язування завдань та завдання для самостійної і домашньої робіт Завдання 1.

1. Знайти наближене значення функції при даному значенні аргумента за допомогою інтерполяційного многочлена Лагранжа, якщо функцію задано: 1) у нерівновіддалених вузлах таблиці; 2) у рівновіддалених вузлах таблиці.