2. Индексный метод при оценке влияния факторов в детерминированном анализе.

Ответ: Основан на относительных показателях динамики, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в плановом (базисном) периоде.

Используется для определения влияния факторов на результативный показатель только в мультипликативных моделях.

Исходная модель .

Общий индекс результативного показателя:

.

Относительное изменение результативного показателя за счет факторов

a, b, c:

; ; .

Абсолютное изменение результативного показателя за счет факторов a, b, c:

;

;

.

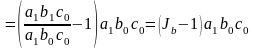Задача

Используя исходную кратную модель коэффициента оборачиваемости активов, определить: среднегодовую величину активов, если выручка от продаж составила 1050 тыс.руб., рентабельность продаж – 18%, рентабельность активов – 36%.

Ответ:

0,36=x \1050

X=378

Пр=378

X=378\0,18=2,100 Ответ: 2100

Билет 20

1. Приемы моделирования исходных факторных систем: удлинение, расширение, сокращение и др.

Ответ: Моделирование - один из важнейших методов научного познания, с помощью которого создается модель (условный образ объекта исследованиия). Сущность моделирования - взаимосвязь исследуемого показателя с факторным в форме математического уравнения. Существует 4 типа факторных моделей: 1) аддативная – результативный показатель представляет собой алгебраическую сумму показателей факторов y=x₁+x₂+…+x _n. , 2) мультипликативная – формализованная модель, в которой результативный показатель – это произведение показателей факторов y=x₁*x₂*…*x _n , 3) кратная – когда результативный показатель это частное показателя факторов y=x₁/x₂ , 4) смешанные или комбинированные модели y=(a+b)/c или y=a*b/c. Для преобразования формализованной модели существует ряд приемов моделирования: удлинение, расширение, сокращение, расчленение. Удлинение (для кратных моделей): удлинение числителя путем замены одного или нескольких факторов на сумму однородных показателей затраты на себестоимость/выручку от продаж = (зарплата + материалы + амортизация)/выручку от продаж. Расширение – умножение числителя и знаменателя дроби на один или несколько новых показателей у = а/в = а*с/в*с . Формула Дюпона: рентабельность активов = рентабельность продаж умножить на коэффициент оборачиваемости активов. Сокращение – деление числителя и знаменателя на одно и тоже число.

2. Классические методы экономического анализа (балансовый метод, детерминированный факторный анализ).

Ответ: Балансовый способ служит для отражения соотношений, пропорций двух групп взаимосвязанных и уравновешенных экономических показателей, итоги которых должны быть тождественными. В АХД балансовый метод используется для проверки правильности определения влияния различных факторов на прирост величины результативного показателя. В детерминированном анализе алгебраическая сумма величины влияния отдельных факторов должна соответствовать величине общего прироста результативного показателя:

Yобщ=∑Yxi

Иногда балансовый способ применяют для определения величины влияния отдельных факторов на прирост результативного показателя. Например, когда из трех факторов известно влияние двух, то влияние третьего можно определить, вычтя от общего прироста результативного показателя результат влияния первых двух факторов:

Yс = Yобщ - Ya - Yb

Факторный анализ – это процесс комплексного, системного исследования влияния факторов на уровень результативных показателей.

Модель факторной сис-мы в общем виде y=f(x₁,x₂,…,x₃)

Типы факторного анализа: 1) Детерминированный и стохастический. 2) Прямой и обратный. 3) Одноуровневый и многоуровневый. 4) Статистический и динамический. 5) Ретроспективный и перспективный (прогнозный).

1. Детерминированный факт. анализ представляет собой методику иссл-я влияния факторов, связь кот. с результативным показателем носит функциональный хар-р. Функциональная связь может быть нескольких видов: аддитивная связь (y=x₁+x₂+…+x_n), мультипликативная связь (y=x₁×x₂×..×x_n), кратная модель (y=a/b), смешанная модель (y=a/b+c). Стохастический анализ исследует влияние факторов, связь кот. с результативным показателем явл. вероятностной (корреляционной).

2. Прямой факт. анализ осуществляется дедуктивным способом - от общего к частному. Он проводится с целью комплексного исследования факторов, формирующих величину изучаемого результативного показателя. Обратный факторный анализ исследует причинно-следственные связи способом логической индукции – от частных, отдельных факторов к общим, от причин к следствиям.

3. Одноуровневый факт. анализ исследует факторы одного уровня (Y=a×b), при многоуровневом проводится детализация факторов a и b на составные элементы с целью изучения их сущности.

4. Статистический анализ применяется при изучении влияния факторов на результативные показатели на определенную дату, а динамический – исследует причинно-следственные связи в динамике.

Задача

Используя исходную кратную модель рентабельности собственного капитала, рассчитать объем годовой выручки от продаж при условии, что собственный капитал составил 1240 тыс. руб., его рентабельность – 60%, рентабельность продаж – 20%.

Решение:

Рентабельность продаж, %

Рентабельность собственного капитала, %

Формула расчета: где

СК – собственный капитал.

0,60=Пр/1240

Пр=0,60*1240=744

0,20=744/выручка

Выручка=3,720

Ответ :объём годовой выручки 3,720

Билет 21

1. Приемы финансового оценивания: настоящая и будущая стоимость денег.

Ответ: Сегодняшние деньги всегда дороже будущих. Сущность метода компаудинга – определение суммы денег, кот. будет иметь инвестор в конце финансовой операции. Заданными величинами здесь явл-ся исходная сумма инвестиций, срок и %-я ставка доходности, искомая величина – сумма средств к получению по завершении фин. операции. Пример: вклад 1000руб. в банк под 20% годовых. Доходность: за 1-й год 1000(1+20%)=1000*1,2=1200т.р.;

за 2-й год 1200(1+20%)=1200*1,2=1440т.р.; за 3-й год 1440(1+20%)=1440*1,2=1728т.р. Или 1000*1,2³=1728т.р. Данный пример показывает методику определения стоимости инвестиций при использовании сложных %. Определение стоимости инвестиций через несколько лет при использовании сложных %: FV=PV(1+r)^t, где FV – будущая ст-сть инвестиций через n лет, PV – первоначальная сумма инвестиций, r – ставка % в виде дроби, t – число лет в расчетном периоде. Выражение (1+r) показывает, сколько будет стоить ден. единица через год, 1/(1+r) – сколько сегодня стоит ден. единица, кот. будет получена через год. Пример: банк ежегодно начисляет сложные % (30%) на вклад 100000 руб. Тогда наращенная сумма через 2 года составит: St= So(1+i)^t=100000(1 + 0,3)² =169000 руб. Ставка сложных % за каждый период года равна i/m, где т - число раз начисления % в году. В этом случае алгоритм расчета наращенной суммы: St=So(1+i/m)^tm, где So - современная ст-сть суммы денег; St - будущее значение суммы денег; t - срок, по истечении кот. современное значение денег из­менится; i - годовая %-я ставка. Чем чаще начисляются %, тем быстрее растет вклад. Начисление процен­тов по простой ставке: FV=PV(1+rn)=1000*(1+0.2*3)=1600т.р. или I=So(1+it). Будущая ст-сть одной ден. единицы при простых % возрастает прямолинейно, при сложных – по экспоненте, что обусловлено начислением от возросшей суммы инвестиций с учетом %. Исходная сумма может быть рассчитана: So=I/1+it. Расчет числа простых %: i=(I/So-1)1/t. Кредитору выгоднее вы­давать ссуду под простой дисконт, а не под простой процент. Простой дисконт представляет собой процентный доход, ко­т. вычитается из ссуды в момент ее выдачи. Пример: ссуда 10000 руб. выдана на полгода под 20% простых годовых. Простой дисконт также 20%. Сумма к возврату под простой процент составит: I= So (1 + it) = 1000 руб. (1 + 0,2*0,5) = 11000 руб. Под простой дисконт: I=So/1-it=10000/1-0.2*0.5=11111руб. Простой процент - отношение суммы приращения за какой-то срок к начальной сумме, он же - ставка процента, эффективность вложений, или интерес креди­тора; дисконт, или относитель­ная скидка, - отношение суммы приращения за определенный срок к наращенной сумме; дисконт-фактор (V) - отношение начальной суммы вложений к наращенной или разность м/у единицей и дисконтом за определенный срок: V=I-d(it)=So/I. Для расчета суммы, кот. клиент получит на руки, если по условиям кредитного договора ссуда выдается под простой дис­конт, надо предполагаемую к возврату сумму умножить на вели­чину дисконт-фактора. Рассчитать современную цен­ность суммы денег можно путем ее дисконтирования: So=I/1+it. При этом происходит абстрагирование от рисков финансовых рынков, инфляции, а во внимание при­нимается возможность использования денег путем инвестирова­ния в банк под простой годовой процент. Годовая ставка носит название номинальной. Пример: в первом контракте сумма обязательства 20 000 руб. исходя из простых 30% в год с выплатой 12000 руб. через два года, ос­тальных 8000 руб. - через пять лет по окончании контракта. Во втором контракте сроком на четыре года под тот же простой процент возврат первой части обязательства в сумме 7000 руб. предусмотрен через год, а остальной суммы - через три года от настоящего момента. Надо рассчитать сумму долга во втором контракте, которая будет возвращена через три года, при условии, что современные ценности потоков платежей в обоих контрактах будут эквивалент­ными, т.е.: S₁¹+S₂¹=S₁²+S₂², где S₁¹+S₂¹- дисконтированные (приведенные) суммы в первом контракте; S₁²+S₂²- дисконтированные суммы платежей во втором контракте. В качестве наращенной суммы (I) принимается сумма обязательства вернуть долг, включая проценты. Тогда приведенная к настоящему мо­менту сумма обязательного платежа составит: S₁¹ = 12000 руб. : (1 + 0,3* 2) = 7500 руб.; S₂¹ = 8000 руб. : (1 + 0,3*5) = 3200 руб.; S₁² = 7000 руб. : (1 + 0,3*1) = 5384,6 руб.; S₂² = Х руб. : (1 + 0,3*3) = Х руб. : 1,9. Контракты будут эквивалентны, если будет выполнено равенство: 7500 руб. + 3200 руб. = 5384,6 руб. + Х руб.: 1,9. Х руб. = (7500 + 3200 - 5384,6) х 1,9 = 10099,3 руб. Сокращение срока платежа во втором кон­тракте позволяет уменьшить суммарные выплаты. По первому кон­тракту они составят 20000 руб. (12000 + 8000), а по второму ­17 099,3 руб. (7000 + 10099,3). В финансовых расчетах с использованием сложных процен­тов принято определять эффективную ставку, т.е. такую годовую номинальную ставку сложных процентов, которая дает возмож­ность получить тот же результат, как и при начислении процен­тов несколько раз в году. Эффективная процентная ставка будет больше номинальной. (1+i_эф)^t=(1+i^m/m)^mt. i_эф=(1+i^m/m)^mt-1. В финансовых расчетах должна учитываться инфляция, тем бо­лее если она значительна. С одной стороны, сумма, положенная, например, на депозит, получит приращение, а с другой - утратит свою реальную стоимость в результате инфляции. Для определения наращенной суммы с учетом инфляции используют алгоритм: Sинф=So*((1+i^m/m)^t/(1+h)^t), где Sинф – наращенная сумма с учетом инфляции, So – базовая сумма, i^m – годовая номинальная банковская ставка, применяемая m раз в году, h – ожидаемый месячный темп инфляции, t – число месяцев. Пример: на депозит положена сумма So=800т.р. i^m = 48%. m=12. h=10%. Определим наращенную сумму через 4 месяца, эрозию капитала (ЭК). Sинф=800т.р.*((1+0,48/12)⁴ /(1+0,1) ⁴)=639,2т.р. ЭК=Sинф-So=639,2т.р. – 800т.р. = -160,8т.р.