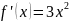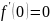16. Лопиталь. Раскрытие

Пусть: 1) определены и непрерывны в некоторой окрестности точки а (за исключением, быть может, самой точки а)

2) точки а (за исключением, быть может, самой точки а), причем

3) Пусть

4) Существует , тогда существует , причем выполняется равенство

Доказательство:

Существует 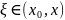такая что

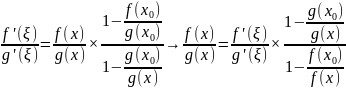
Замечание 1: теорема имеет место при

Замечание 2: если при применении правила сохраняется неопределенность, то при выполнении условий теоремы можно повторить правило Лопиталя.

Пример:

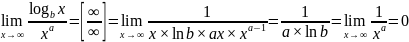
17. Лопиталь. Раскрытие

А) 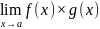, если

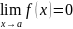
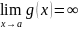
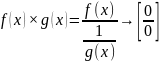
B) , если

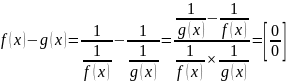
18. Лопиталь. Раскрытие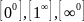

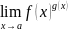
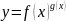
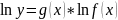
19. Формула Тейлора

Пусть n раз дифференцируема в окрестности точки Х₀

Представление в виде «близкого» многочлена 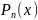(аппроксимация)

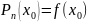
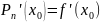
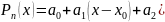
Если

Если

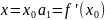
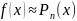
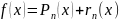
Если , то

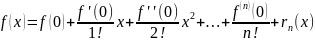– формула Маклорена

– формула Пеано

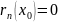
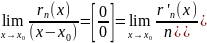
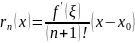– формула Лагранжа

20. Разложение функции 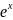по формуле Тейлора.

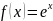
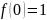
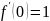
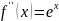
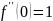
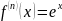
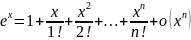
21. Разложение функции по формуле Тейлора.

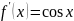
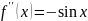
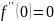
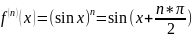
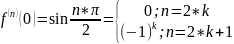
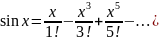
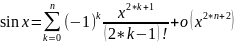
22. Разложение функции по формуле Тейлора.

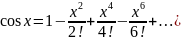
23. Разложение функции по формуле Тейлора.

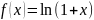
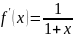
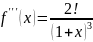
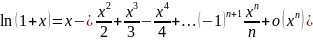
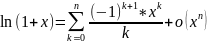
24. Разложение функции 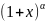по формуле Тейлора.

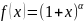
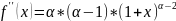
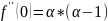
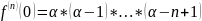
25. Исследование функции на монотонность

Определение 1: называется неубывающей на промежутке Х, если для любых выполняется

Определение 2: называется строго возрастающей на промежутке Х, если для любых

выполняется

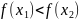
Определение 3: называется невозрастающей на промежутке Х, если для любых выполняется

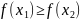
Определение 2: называется строго убывающей на промежутке Х, если для любых

выполняется

Необходимое и достаточное условие монотонности

Для того, чтобы дифференцируемая функция на Х была возрастающей (убывающей), необходимо и достаточно, чтобы

Доказательство:

• Необходимость: пусть возрастает на промежутке Х

Возьмем , причем ⇒

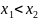По теореме Лагранжа существует такая точка ξ, принадлежащая отрезку 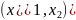, что

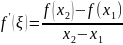
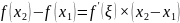
• Достаточность: пусть 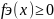на промежутке Х

Применим теорему Лагранжа на

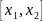
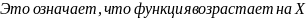
Достаточное условие строгой монотонности

Пусть для дифференцируемой на промежутке Х выполняется 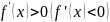, тогда строго возрастает (строго убывает) на промежутке Х.

Доказательство:

Пусть дифференцируема на промежутке Х и выполняется

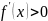
Применим теорему Лагранжа на , тогда существует такая точка ξ, принадлежащая отрезку , что

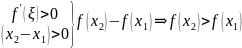– строгое возрастание

Замечание: обратная теорема не имеет места, т.е. если ⇏

Пример: