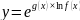1. Производная. Геометрический и физический смысл. Правила диференцирования

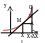Производная y=f(x) определена на некоторой прямой Х

∆Х - приращение

Старое значение - f(x)

Новое значение – f(x₀+∆x)

Приращение y =∆y= f(x₀+∆x) – f(x₀)

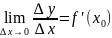- определение производной.

Выражает скорость изменения фунукции.

; ;

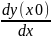Геометрический смысл производной

K=tgα=f’(x₀)

Y=f(x₀) + f’(x₀)(x-x₀)

Физический смысл производной

Правила дифференцирования

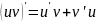
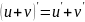
Правило сложной функции

Y(U), где U=U(x)

y(U(x))- сложная функция

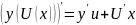
2. Дифференцируемость в точке. Связь с

существованием производной

Пусть F(x) определена в некоторой окрестности Х₀

Определение: Функция y=f(x) называется дифференцируемой в точке Х₀, если в окрестности этой точки выполняется равенство

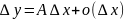
Теорема (о связи дифференцируемости и существовании производной)

Для того, чтобы f(x) была дифференцируема в точке Х₀, необходимо и достаточно, чтобы существовала конечная производная в этой точке и выполнялось равенство

Доказательство:

Необходимость: Пусть f(x) дифф. в т. Х₀, это означает

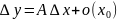
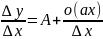
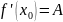
Достаточность: Пусть существует

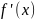
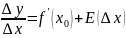
O(∆x)

Замечание:

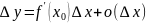
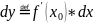
dy

3. Дифференцируемость в точке. Связь с

непрерывностью

Пусть F(x) определена в некоторой окрестности Х₀

Определение: Функция y=f(x) называется дифференцируемой в точке Х₀, если в окрестности этой точки выполняется равенство

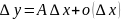
Теорема о связи дифференцируемости с непрерывностью

Пусть 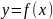диффер. в т. Х₀, тогда непрерывна в т. Х₀

Доказательство: Пусть дифф. в т. Х₀, тогда выполняется

при

означает непрерывность

Обратная теорема не имеет места

Пример:

В X₀=0 (не существует производная, т.к. нет касательной)

4. Дифференцируемость в точке. Геометрический смысл

Пусть F(x) определена в некоторой окрестности Х₀

Определение: Функция y=f(x) называется дифференцируемой в точке Х₀, если в окрестности этой точки выполняется равенство

Геометрические свойства дифференциала

Дифференциал численно равен приращению ординаты касательной

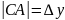
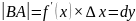
5. Дифференцируемость в точке. Инвариантность формы

Пусть F(x) определена в некоторой окрестности Х₀

Определение: Функция y=f(x) называется дифференцируемой в точке Х₀, если в окрестности этой точки выполняется равенство

Инвариантность формы дифференциала

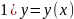, где Х-аргумент, независимая переменная

, где dx – приращение

2) , но

Получается

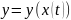
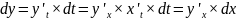, где dx – дифференциал

Смысл инвариантности: формула сохраняется не зависимо от того, является ли Х независимой переменной или функцией

6. Дифференцирование функции, заданной параметрически

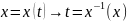
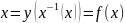
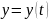, где

)

Пример 1: Пример 2:

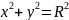
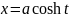
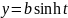
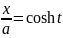
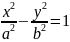
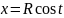
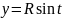
7. Дифференцирование показательно-степенных функций

1.

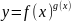
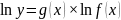
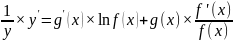
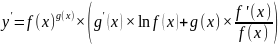
2.