8.Нечетко-логические экспертные системы: обобщенная структурная схема, назначение отдельных модулей, пример функционирования.
Общая структура устройств нечеткого логики
Микроконтроллер нечеткой логики
Общая структура микроконтроллера, использующего нечеткую логику, показана на рис.1. Она содержит в своем составе следующие составные части:
· блок фаззификации;
· базу знаний;
· блок решений;
· блок дефаззификации.
Блок фаззификации преобразует четкие (сrisp) величины, измеренные на выходе объекта управления, в нечеткие величины, описываемые лингвистическими переменными в базе знаний.
Блок решений использует нечеткие условные (if – then) правила, заложенные в базе знаний, для преобразования нечетких входных данных в требуемые управляющие воздействия, которые носят также нечеткий характер.
Блок дефаззификации преобразует нечеткие данные с выхода блока решений в четкую величину, которая используется для управления объектом.
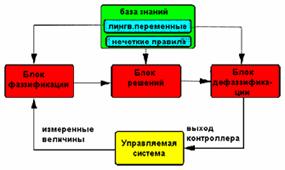
Рис.1. Общая структура нечеткого микроконтроллера.
Процессор нечеткой логики
Аппаратный процессор нечеткой логики второго поколения принимает аналоговые сигналы, переводит их в нечеткий формат, затем, применяя соответствующие правила, преобразует результаты в формат обычной логики и далее – в аналоговый сигнал. Все это осуществляется без внешних запоминающих устройств, преобразователей и какого бы ни было программного обеспечения нечеткой логики.
9.Способы суперпозиции и дефаззификации в процессе нечеткого логического вывода.
Дефаззификация.
Техника нечеткого логического вывода, примененная к информации, собранной на предыдущих этапах, позволяет вычислить показатель, который прогнозируется, в виде нечеткого множества. Это нечеткое множество определяет уровень выхода биогаза для фиксированного вектора влияющих факторов. Чтобы перейти от полученного нечеткого множества к количественной оценке нужно выполнить процедуру дефаззификации, т. е. преобразования нечеткой информации в четкую форму. Среди разных методов дефаззификации наиболее распространенным является нахождение "центра масс" плоской фигуры, ограниченной функцией принадлежности нечеткого множества и горизонтальной координатой. Модель нечеткого логического вывода вместе с процедурой дефаззификации обеспечивает возможность наблюдения за изменением выходного показателя при вариации влияющих факторов.
http://tinyurl.com/avwupe5
Суперпозиция.
Традиционно суперпозиция функций принадлежности нечетких множеств определяется как их объединение. Другой метод суперпозиции состоит в суммировании значений всех функций принадлежности. Самым простым (но и наименее часто используемым) является подход, когда суперпозиция не производится. Выбирается одно из правил вывода, результат которого используется в качестве интегрального результата.
При переходе от нечеткого вывода к четкому выходу могут использоваться различные способы:
· метод центра тяжести (определяется абсцисса центра тяжести кривой по функцией принадлежности);
· метод первого максимума (выбирается первый элемент нечеткого множества при котором достигается максимум значения функции принадлежности);
· метод среднего максимума;
· метод наименьшего максимума.
10.Основы нечеткой арифметики: правила выполнения арифметических операций с нечеткими числами, пример.
Определение. Нечетким числом α будем называть множество принимаемых значений v1,v2,…,vk и вероятностей p1, p2, …, pk того, что нечеткое число будет принимать соответствующее значение.
Сложение двух нечетких чисел.
Пусть α и β два нечетких числа. Тогда определим их сумму α + β по правилу α + β = γ, где множество принимаемых значений будет состоять из k^2 чисел Vai+Vbj с соответствующими вероятностями Pai*Pbj.
Вычитание двух нечетких чисел.
Пусть α и β два нечетких числа. Тогда определим их разность α - β по правилу α - β = γ, где множество принимаемых значений будет состоять из k^2 чисел Vai-Vbj с соответствующими вероятностями Pai*Pbj.
Умножение двух нечетких чисел.
Пусть α и β два нечетких числа. Тогда определим их разность α * β по правилу α * β = γ, где множество принимаемых значений будет состоять из k^2 чисел Vai*Vbj с соответствующими вероятностями Pai*Pbj.
Деление двух нечетких чисел.
Пусть α и β два нечетких числа. Тогда определим их разность α / β по правилу α / β = γ, где множество принимаемых значений будет состоять из k^2 чисел Vai/Vbj с соответствующими вероятностями Pai*Pbj.
Свойства
«От перестановки слагаемых сумма не меняется»
α + β = β + α
Возьмём 2-а нечётких числа α и β, α + β = γ, где множество принимаемых значений будет состоять из k2 чисел Vai+Vbj с соответствующими вероятностями Pai*Pbj. Если же рассмотреть выражение β + α, оно также будет равно у, ведь условия существование наших чисел не менялось, изменилась только позиция значений чисел Vbj+Vai отсюда следует α + β = β + α.
«От перестановки множителей произведение не меняется»
α * β = β * α
Возьмём 2-а нечётких числа α и β, α * β = γ, где множество принимаемых значений будет состоять из k^2 чисел Vai+Vbj с соответствующими вероятностями Pai*Pbj. Если же рассмотреть выражение β * α, оно также будет равно у, ведь условия существование наших чисел не менялось, отсюда следует α * β = β * α.