6.Лингвистическая переменная: определение, структура, связь с нечеткими множествами.

Лингвистическая переменная — в теории нечётких множеств, переменная, которая может принимать значения фраз из естественного или искусственного языка. Например, лингвистическая переменная «скорость» может иметь значения «высокая», «средняя», «очень низкая» и т. д. Фразы, значение которых принимает переменная, в свою очередь являются именами нечетких переменных и описываются нечетким множеством.

Лингвистическая переменная характеризуется набором свойств  , в котором:

 — название переменной;

 обозначает терм-множество переменной  , т.е. множество названий лингвистических значений переменной  , причем каждое из таких значений является нечеткой переменной   со значениями из универсального множества   с базовой переменной   ;

 — синтаксическое правило, порождающее названия   значений переменной   ;

 — семантическое правило, которое ставит в соответствие каждой нечеткой переменной   ее смысл  , т.е. нечеткое подмножество  универсального множества  .

Конкретное название  , порожденное синтаксическим правилом  , называется термом. Терм, который состоит из одного слова или из нескольких слов, всегда фигурирующих вместе друг с другом, называется атомарным термом. Терм, который состоит из более чем одного атомарного терма, называется составным термом.

Пример. Рассмотрим лингвистическую переменную с именем   "ТЕМПЕРАТУРА В КОМНАТЕ". Тогда оставшуюся четверку  , можно определить так:

универсальное множество U=[5,35];

терм-множество T={"ХОЛОДНО", "КОМФОРТНО", "ЖАРКО"} с такими функциями принадлежностями:

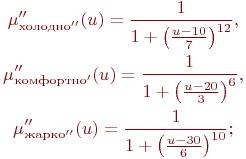
синтаксическое правило  , порождающее новые термы с использованием квантификаторов "и", "или", "не", "очень", "более-менее" и других;

 будет являться процедурой, ставящей каждому новому терму в соответствие нечеткое множество из   по правилам: если термы   и   имели функции принадлежности   и   соответственно, то новые термы будут иметь следующие функции принадлежности, заданные в таблице:

Квантификатор	Функция принадлежности (   )
не
очень
более-менее
и
или

http://tinyurl.com/b7mwwkn -продолжение http://tinyurl.com/acdh4cf -дополнение

7.Рассуждения на нечетких множествах. Правила нечеткой импликации. Примеры.

Нечеткие отношения

Пусть Е = Е₁Е₂ ...Е_n - прямое произведение универсальных множеств и М - некоторое множество принадлежностей (например М = [0,1]). Нечеткое n-арное отношение определяется как нечеткое подмножество R на E, принимающее свои значения в М. В случае n = 2 и М = [0,1], нечетким отношением R между множествами X = Е₁ и Y = Е₂ будет называться функция R:(X,Y)  [0,1], которая ставит в соответствие каждой паре элементов (х,y) XY величину _R(x,y) [0,1].

Обозначение: нечеткое отношение на XY запишется в виде: xX, yY: xRy. В случае, когда X = Y, т.е. X и Y совпадают, нечеткое отношение R: XX  [0,1] называется нечетким отношением на множестве X.

Примеры.

1. Пусть X = {x₁,x₂,x₃}, Y = {y₁,y₂,y₃,y₄}, М = [0,1]. Нечеткое отношение R=XY может быть задано, например, как показано в таблице 4.2.

Таблица 4.2 - Задание нечеткого отношения

	y1	y2	y3	y4
x1	0	0	0.1	0.3
x2	0	0.8	1	0.7
x3	1	0.5	0.6	1

2. Пусть X = Y = (-,), т.е. множество всех действительных чисел. Отношение x>>y (x много больше y) можно задать функцией принадлежности:

3. Отношение R, для которого _R(x,y) = e^-k(x-y)2, при достаточно больших k можно интерпретировать так: «x и y близкие друг к другу числа».

Нечеткая импликация

Пусть имеем обычные («четкие») высказывания вида: p = «x есть A» и q = «y есть B». Тогда импликацией (в обычной, «четкой» логике) «если p, то q» называется предложение, которое ложно тогда и только тогда, когда p истинно, а q ложно.

Такой вид отношений между высказываниями обычно обозначается как и понимается как утверждение «p влечет за собой q».

Если перейти к бинарной (булевой) алгебре логики, где с понятием «истина» сопоставляется 1, а с понятием «ложь» - 0, то импликацию можно представить логической формулой

,

или таблицей истинности:

p	q
1	1	1
0	1	1
0	0	1
1	0	0

Более полная трактовка понятия импликации означает, что истинность - это тоже, что истинность утверждения «степень истинности q не меньше, чем степень истинности p», т.е.

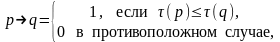
где - и - указанные «степени истинности» (в четкой логике принимающие значения лишь 0 или 1).

Пример - 18. Пусть p = «x больше 5» и q = «x больше 4». Легко видеть, что в данном случае импликация является истинной, поскольку из неравенства x>5 следует неравенство x>4.

Нечеткая импликация, в принципе сохраняет тот же смысл, что и импликация четкой логики. Отличие состоит лишь в том, что в этом случае «степени истинности» могут иметь любое значение между 0 и 1.

Нечеткая импликация определяется обычно следующим образом.

Будем считать, что заданы универсальные множества X и Y, содержащие конечное число элементов. Под способом определения нечеткой импликации «если А, то В», где А и В - нечеткие множества на X и Y соответственно (например: «если температура - большая, то скорость близка к нулю»), будем понимать способ задания нечеткого отношения R на XY, соответствующего данному высказыванию.

Такое отношение можно задать по-разному, поэтому для математического представления нечеткой импликации предложено большое число различных формул, некоторые из которых вместе с фамилиями предложивших их авторов приведены ниже [18]:

Ларсен (Larsen): .

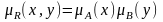Лукасевич (Lukasiewicz): .

Мамдани (Mamdani): .

Брауэра:

Гёдель (классическая нечеткая импликация):

.

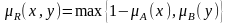В общем, какого-либо преимущества одной формулы над другими нет, поэтому все они (а к настоящему времени известно несколько десятков подобных формул) имеют право на существование.