1. Метод проекций

Проецирование – это процесс, в результате которого получают изображения, представляющие собой проекции на плоскости.

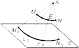
1. Проецирование центральное. Центральным называется проецирование, при котором все проецирующие лучи выходят из одной точки S, называемой центром проецирования. Построение центральных проекций прямой линии АВ и кривой MN показано.

 2. Проецирование параллельное. Параллельным называется проецирование, при котором все проецирующие лучи между собой параллельны.

Параллельные проекции могут быть косоугольными (рис.1.7) и прямоугольными (рис. 1.8).

S – направление проецирования.

Прямоугольное (ортогональное) проецирование является частным случаем параллельного. Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и кроме того, справедлива теорема о проецировании прямого угла: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол.

Метод монжа Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей.

2. Точка в системе двух плоскостей проекций

На рис. показано построение проекций некоторой точки А в системе 1, 2. Проведя из А перпендикуляры к оси, получаем проекции точки А:горизонтальную, обозначенную А', и фронтальную, обозначенную А". Проецирующие прямые, соответственно перпендикулярные к 1 и 2,определяют плоскость, перпендикулярную к плоскостям и к оси проекций. Эта плоскость в пересечении с 1 и 2 образует две взаимно перпендикулярные прямые А'АХ и А"АХ, пересекающиеся в точке Ах на оси проекций.

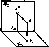
ТОЧКА В СИСТЕМЕ ТРЕХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ 1, 2, 3

Рассмотрим введение в систему 1 ^ 2 еще одной плоскости проекций обозначенная буквой 3 плоскость перпендикулярна и к 1 и к 2. Ее называют профильной плоскостью проекций. Помимо оси проекций х, появляются еще оси z и у, перпендикулярные к оси х. Буквой О обозначена точка пересечения всех трех осей проекций.

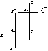
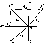
3. Прямые общего положения

Прямая  не параллельная ни одной из плоскостей проекций, называется прямой общего положения. Прямая восходящая - ее признаком является одинаковое направление проекций прямой относительно оси х, а нисходящей - разное Прямая общего положения нисходящая - у нее одинаковое направление проекций прямой относительно оси z, а у восходящей -  разное

а)

а)

б)

б)

Рис. 1. Прямые общего положения: а) восходящая, б) нисходящая на наглядном и комплексном чертежах

ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ

Прямые параллельные или перпендикулярные координатным плоскостям проекций называются прямыми частного положения. Они делятся на: ПРЯМЫЕ УРОВНЯ- прямые параллельные координатным плоскостям проекций и на ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ - это прямые перпендикулярные координатным плоскостям проекций.

ГОРИЗОНТАЛЬ (h // H)   ФРОНТАЛЬ (f // V) ПРОФИЛЬНАЯ ПРЯМАЯ (P // W)