Вибір системи числення

У комп'ютерах в основному використовують однорідні позиційні системи чис­лення, при виборі основи q цих систем враховують такі показники:

1. Наявність фізичних елементів для зображення цифр системи у вигляді од­ного із q станів, наприклад, різниці напруг. Зменшення числа станів спрощує фізичний елемент, тому найбільш сприйнятою є двійкова система.

2. Економічність системи числення. Система з більшою основою q забезпечує представлення певного числа меншою кількістю розрядів. Але при цьому ускладнюється побудова фізичного елемента з більшим числом станів.

Ефективність системи числення з основою , оцінюється кількістю циф­рових розрядів , необхідних для зображення певного числа з довжиною 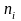, тобто . При цьому враховується, що зменшення значення призводить до зменшення електронних схем для представлення чисел в комп'ютерах.

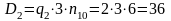Для представлення будь-якого десяткового числа довжиною, напри­клад використовують цифророзрядів. У двійковій системі для представлення того ж числа (з врахуванням співвідношен­ня ) потрібно мати цифрових розрядів.

Найбільш економічною є система з основою q= 2.73 ... ≈ 3. Двійкова система економічно поступається трійковій на 5,8%, проте має надійніші фі­зичні елементи. Крім того, для запам'ятовування цифр трійкової системи 0, 1, 2 використовують два двійкових фізичних елементи. Із цього виходить, що найефективнішою є двійкова система числення.

3. Трудомісткість і швидкодія виконання арифметичних операцій. Чим менша основа q, тим менше цифр бере участь в обчисленні даних і тим вища швидкодія комп'ютера. Наприклад, швидкодія машини в двійковій системі перевищує швидкодію в трійковій на 26,2%. а в десятковій — у 2,7 раза.

4. Наявність формального математичного апарату для аналізу і синтезу циф­рових схем. Таким апаратом для двійкових елементів є булева алгебра.

Таким чином, з перерахованих показників видно, що найприйнятнішою для застосування в комп'ютерах є однорідна позиційна двійкова система числення. Двійко-системи числення використовують у великих і середніх комп'ютерах, призначених розв'язання науково-технічних задач з великим об'ємом обчислень і порівняно малою кількістю початкових даних.

Двійково-десяткову систему застосовують для розв'язання економічних задач, характеризуються великим об'ємом вхідних і вихідних даних порівняно з малим об’ємом розрахунків.

Двійково-десяткова система має такі достоїнства:

• не потрібне переведення початкових даних з однієї системи в іншу;

• зручність контролю результатів зображенням їх на екрані дисплея;

• зручність автоматичного контролю через наявність надлишкових кодів у зо­браженні цифр 1010, 1011,…,1111

Загальні відомості про системи числення

Система числення - сукупність прийомів і правил для зображення чисел за допомогою символів (цифр), що мають певне кількісне значення. Залежно від способів зображення чисел цифрами системи числення діляться на непозиційні і позиційні. В ЕОМ застосовуються позиційні системи числення. Непозиційні системи числення у ОТ не використовуються через свою громіздкість і складність правил виконання дій.

Позиційною системою числення називається така, в якій кількісне значення кожної цифри залежить від її позиції (місця) в числі. Прикладом може служити звичайна (арабська) десяткова система числення. Наприклад, число 373, представлене в десятковій системі числення, має в молодшому і самому старшому розрядах цифру 3. Цифра 3 в старшому розряді має вагу в 100 разів більше, ніж в молодшому розряді. В позиційній системі числення будь-яке число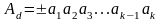 може бути подано у вигляді наступної суми:

, де k - загальна кількість розрядів в зображені числа; a_i- цифра і - го розряду; d - основа системи числення;

і - порядковий номер розряду.

Цифри, необхідні для побудови системи числення, повинні задовольняти нерівність . Основою системи числення d називається кількість знаків або символів, що використовуються для зображення числа в даній позиційній системі числення. За основу d можна прийняти будь-яке число.

Для десяткової системи числення d=10.

Десяткове число 897,346 можна представити у вигляді наступної суми:

8 9 7 3 4 6

коефіцієнти

Таким чином, десяткове число є сумою різних ступенів десяти з відповідними коефіцієнтами. Ці коефіцієнти зображають число 897,346 у вигляді скороченого запису. Використовування в ЕОМ позиційних системах числення дозволяє значно спростити зображення чисел і операції з ними.

Від вибору системи числення при проектуванні ЕОМ залежать такі її характеристики, як швидкість обчислень, об'єм пам'яті, складність алгоритмів виконання арифметичних операцій. З погляду технічної реалізації якнайкращою є двійкова система числення, оскільки для побудови ЕОМ знайшли широке застосування двохпозиційні елементи. Двійкова система числення в ЕОМ є основною системою числення, в якій здійснюються арифметичні і логічні перетворення інформації в пристроях ЕОМ. Будь-яке число з двійкової системи числення може бути переведено в десяткову за допомогою формули розкладання:

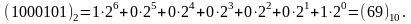
Основним недоліком використовування двійкової системи числення є необхідність переведення початкових числових даних з десяткової системи числення в двійкову, а результатів виконання дій - з двійкової системи числення в десяткову. Операції, пов'язані з переведенням чисел в двійкову систему числення і назад, виконуються ЕОМ по спеціальних підпрограмах з використанням допоміжної двійково-десяткової системи числення.