2.8. Перестановки с повторениями

М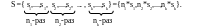 ножество, которое может содержать одинаковые элементы, называется мультимножеством. Например М={1,1,2,3,1,2,3} - мультимножество, которое содержит элементы 1, 2 и 3, причём элемент 1 входит в мультимножество 3 раза, а элементы 2 и 3 – по два раза. Мультимножества равны, если они состоят из одних и тех же элементов, поэтому {1,1,2,3,1,2,3}={1,1,1,2,2,3,3}, т.е. порядок расположения элементов не важен. Мультимножество, состоящее из конечного числа элементов, называется конечным. Количество элементов в мультимножестве S называется мощностью мультимножества и обозначается |S|. Мощность мультимножества М={1,1,2,3,1,2,3} равна семи, |M|=7. Количество n_iвхождений элемента s_i в мультимножество S называется кратностью элемента. Конечное мультимножество S будем записывать в следующем виде:

Здесь все s_i различны и k_i – кратность элемента s_i. Тогда мощность S равна . Учитывая введённое обозначение, мультимножество М={1,1,2,3,1,2,3} можно записать так: {3*1,2*2,2*3}.

Перестановкой с повторениями называется расположенные в определенном порядке элементы мультимножества.

Теорема 2.6. Число перестановок с повторениями для мультимножества S={n₁*s₁,n₂*s₂,...,n_k*s_k} выражается формулой , где .

Доказательство. Рассмотрим одну перестановку мультимножества и заменим в ней все одинаковые элементы разными. Тогда, число различных перестановок, которые можно составить из рассматриваемой, равно n₁!n₂!…n_k!. Проделав это для каждой перестановки, получим n! перестановок. Следовательно, P_n(n₁,n₂,…,n_k)n₁!n₂!…n_k!=n!. Отсюда

Алгоритм 2.6 (рис.2.13) порождения всех перестановок с повторениями практически не отличается от алгоритма 2.2 порождения всех перестановок множества, за исключением того, что в алгоритме 2.6 обрабатывается мультимножество.

Определим мультимножество С, являющееся результатом разности мультимножеств А и В (С=А-В). Если элемент универсума не принадлежит мультимножеству, то будем считать, что его кратность равна нулю. Элемент xC, если кратность k_А элемента x в мультимножестве А больше кратности k_В элемента x в мультимножестве В и кратность k_С элемента x в мультимножестве С определяется по формуле k_C=k_A-k_B.

Алгоритм 2.6 порождения перестановок с повторениями.

Вход: М – мультимножество, элементы которого можно поставить на i-ое место;

i – заполняемое место в последовательности Р.

Выход: последовательность всех перестановок с повторениями.

Глобальные параметры: Р – формируемая перестановка с повторениями;

n – мощность мультимножества.

Р_i:= x

Перестановка(М-{x},i+1)

Рис.2.13. Рекурсивный алгоритм порождения перестановок

с повторениями

Пусть задано мультимножество {1,1,2,2}={2*1,2*2} и требуется получить все перестановки с повторениями. Это мультимножество содержит элементы 1 и 2 кратности 2. Схема получения всех перестановок по алгоритму 2.6 представлена на рис.2.14. В этой схеме формируемые перестановки заключены в круглые скобки, а мультимножества, элементы которых можно поставить на очередное место в перестановке – в фигурные. В исходной ситуации все места перестановки неопределенны и на первое место можно поставить любой элемент мультимножества: 1 или 2. В схеме к стрелкам приписаны номера действий. В результате выполнения действия 1 на первое место перестановки устанавливается элемент 1, а на второе место после этого можно поставить любой элемент мультимножества {1,2,2}. После выполнения действия 2 на второе место перестановки устанавливается элемент 1, а на третье место после этого можно поставить любой элемент мультимножества {2,2}. После выполнения действий 3 и 4 первая перестановка {1,1,2,2} сформирована. Затем выполняется 3 шага назад и действие 5, ставящее второй элемент из мультимножества {1,2,2} на третье место, после чего на четвёртое место можно поставить любой элемент из мультимножества {1,2}. Далее, после последовательного выполнения действий 6 и 7 вторая перестановка {1,1,2,1} сформирована. Аналогичным образом формируются все остальные перестановки.

{1,1,2,2}

(?,?,?,?)