
- •Оглавление
- •1. Множества
- •1.1. Основные понятия
- •1.2. Способы задания множеств
- •1.3. Операции над множествами
- •Приоритеты операций над множествами
- •1.4. Свойства операций над множествами
- •1.5. Методы доказательства теоретико-множественных тождеств
- •1.5.1. Метод двух включений
- •1.5.2. Метод эквивалентных преобразований
- •1.5.3. Метод характеристических функций
- •1.5.4. Метод логических функций
- •1.5.5. Теоретико-множественный метод
- •1.6. Способы представления множества в памяти эвм
- •1.7. Алгоритмы реализации операций над множествами
- •Практическое занятие 1.1 Операции над множествами
- •Задания
- •Варианты заданий
- •Практическое занятие 1.2 Теоретико-множественные тождества
- •Задания
- •Варианты заданий
- •Контрольные вопросы
- •2. Комбинаторные объекты
- •2.1. Введение
- •2.2. Метод поиска с возвращением
- •2.3. Подмножества
- •2.4. Перестановки
- •2.5. Размещения
- •2.6. Размещения с повторениями
- •2.7. Сочетания
- •2.8. Перестановки с повторениями
- •2.9. Сочетания с повторениями
- •2.10. Упорядоченные разбиения множества
- •2.11. Разбиения множества
- •2.12. Использование алгоритмов порождения комбинаторных объектов при проектировании полнопереборных алгоритмов решения задач выбора
- •2.13. О неэффективности полнопереборных алгоритмов. Пример
- •Времена обработки деталей на станках a и b
- •Времена окончания обработки деталей на станках a и b
- •Времена окончания обработки деталей на станках a и b
- •Времена окончания обработки деталей на станках a и b
- •Практическое занятие 2.1 Алгоритмы порождения комбинаторных объектов
- •Задания
- •Практическое занятие 2.2 Разбиения множеств
- •Задания
- •Количество упорядоченных разбиений
- •Практическое занятие 2.3
- •Задачи выбора
- •Цель занятия: приобретение практических навыков в использовании алгоритмов порождения комбинаторных объектов при проектировании алгоритмов решения задач выбора.
- •Задания
- •Варианты заданий
- •Контрольные вопросы
- •Библиографический список
2.7. Сочетания
Сочетанием из n элементов по k называется k-элементное подмножество n-элементного множества.
Теорема 2.5.
Количество всех различных сочетаний
из n
элементов по k
определяется формулой
![]() .
.
Доказательство.
Можно получить все
![]() размещений,
упорядочив всеми возможными способами
каждое из
размещений,
упорядочив всеми возможными способами
каждое из
![]() сочетаний. Количество способов
упорядочивания одного сочетания равно
k!,
следовательно
=
k!
. Отсюда
сочетаний. Количество способов
упорядочивания одного сочетания равно
k!,
следовательно
=
k!
. Отсюда
![]() .
.
Пусть элементами множества М являются натуральные числа от 1 до n. Для сокращения записи такое множество будем обозначать {1..n}.
Рассмотрим
алгоритм порождения сочетаний в
возрастающем лексикографическом
порядке, т.е. в порядке, когда в каждом
сочетании элементы расположены в порядке
возрастания слева направо, а каждое
следующее сочетание больше предыдущего
(при
сравнении одно сочетание рассматриваем
как число).
Например, сочетания из шести элементов
по три (![]() ),
в возрастающем лексикографическом
порядке запишутся следующим образом:
),
в возрастающем лексикографическом
порядке запишутся следующим образом:
123 135 234 256
124 136 235 345
125 145 236 346
126 146 245 356
134 156 246 456
Сочетания в лексикографическом порядке можно порождать, используя метод поиска с возвращением. Начиная с 1-го места будем последовательно формировать элементы сочетания С. На первое место в сочетании можно ставить элементы из множества {1..n-k+1}. Формирование i-го элемента сочетания опишем рекурсивным алгоритмом 2.5, блок-схема которого представлена на рис.2.11. В цикле перебираются элементы множества {b..n-k+i}, которые можно поставить на i-ое место. Если на i-ое место поставлен элемент x, то минимальный элемент, который можно поставить на i+1–ое место, равен x+1. Если заполнено k-ое место, то сочетание сформировано и выводим его, иначе заполняем следующее i+1-ое место по алгоритму 2.5.
Алгоритм 2.5 порождения сочетаний из n элементов по k.
Вход: i – заполняемое место в сочетании С;
b – минимальный элемент, который можно поставить на i-ое место.
Выход: последовательность всех сочетаний из n элементов по k в возрастающем лексикографическом порядке.
Глобальные параметры: С – формируемое сочетание;
n – мощность множества.
k – количество элементов в сочетании.
Ci
:=
x

 +
+
Сочетание
(i+1,
x+1)
Рис.2.11. Рекурсивный алгоритм порождения сочетаний
из n элементов по k
Пусть задано множество {1,2,3,4,5} и требуется получить все его сочетания по 3. Схема получения всех сочетаний по алгоритму 2.5 представлена на рис.2.12. В этой схеме представлены формируемые сочетания и множества, элементы которых можно поставить на очередное место в сочетании. В исходной ситуации все места сочетания неопределенны и на первое место можно поставить любой элемент множества {1,2,3}. В схеме к стрелкам приписаны номера действий. В результате
выполнения действия 1 на первое место сочетания устанавливается элемент 1, а на второе место после этого можно поставить любой элемент множества {2,3,4}. После выполнения действия 2 на второе место сочетания устанавливается элемент 2, а на третье место после этого можно поставить любой элемент множества {3,4,5} (действие 3) и первое сочетание {1,2,3} сформировано. Затем выполняется шаг назад и действие 4, ставящее элемент 4 из множества {3,4,5} на третье место и второе сочетание {1,2,4} сформировано. Аналогичным образом формируются все остальные сочетания. Действия 1, 11 и 17 заполняют первое место сочетания, действия 2, 6, 9, 12, 15 и 18 – второе место, действия 3, 4, 5, 7, 8, 10, 13, 14, 16 и 19 – третье место.
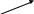 сочетание
сочетание
3 {1,2,3)
множество

 {3,4,5}
4 сочетание
{3,4,5}
4 сочетание
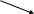 сочетание
{1,2,4)
сочетание
{1,2,4)
{1,2,?} 5
2 сочетание
{1,2,5)
 множество
множество 7
сочетание
множество
множество 7
сочетание
{2,3,4} 6 {4,5} {1,3,4)

 сочетание
сочетание 8
сочетание
сочетание 8
 {1,?,?}
{1,3,?}
сочетание
{1,?,?}
{1,3,?}
сочетание
9 {1,3,5)
1 множество
{5} 10 сочетание
сочетание {1,4,5)
множество {1,4,?}
{1,2,3}
с очетание 11 множество 13 сочетание
 {?,?,?}
12 {4,5}
{2,3,4)
{?,?,?}
12 {4,5}
{2,3,4)
множество сочетание 14
{3,4} {2,3,?} сочетание
сочетание 15 {2,3,5)
17 {2,?,?} множество
{5} 16 сочетание
 сочетание
{2,4,5)
сочетание
{2,4,5)
{2,4,?}
множество множество
{4} 18 {5} 19 сочетание
сочетание сочетание {3,4,5)
{3,?,?} {3,4,?}
Рис.2.12. Схема получения всех сочетаний по алгоритму 2.5
