19. Проводники и диэлектрики в электростатическом поле

Проводники: При внесении проводника в ЭстП происходит перераспределение свободных электронов под действием сил внешнего ЭП, в результате чего на противоположных сторонах проводника равные по величине но противоположные по знаку заряды. (?). Это явление называется электростатической индукцией. После полного перераспределения в проводнике наблюдается следующее: *внутри проводника результирующее электрическое поле равно 0; *вся внутренняя область проводника и его поверхность имеет один и тот же потенциал; *силовые линии результирующего ЭстП перпендикулярны поверхности проводника в каждой его точке; *нескомпенсированный заряд распределен точно по поверхности проводника.

Диэлектрики: Внесение всех трех групп диэлектриков во внешнее электрическое поле приводит к возникновению отличного от нуля результирующего электрического момента диэлектрика или, иными словами, к поляризации диэлектрика. Поляризацией диэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей. 3 вида поляризации: 1) электронная (возникновение у атомов индуцированного дипольного момента за счет деформации электронных орбит); 2) ориентационная (ориентация имеющихся дипольных моментов молекул по полю); 3) ионная (смещение подрешетки положительных ионов вдоль поля, а отрицательных – против поля, приводящем к возникновению дипольных моментов.

20. Поляризованность

Поместим пластину из однородного диэлектрика во внешнее электрическое поле созданное двумя бесконечными параллельными разноименно заряженными плоскостями. Во внешнем электрическом поле диэлектрик объемом V поляризуется, т.е. приобретает дипольный момент 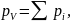где - дипольный момент одной молекулы. Для количественного описания поляризации диэлектрика используется векторная величина – поляризованность – которая определяется как дипольный момент единицы объема диэлектрика

. В случае изотропного диэлектрика поляризованность (для большинства диэлектриков за исключением сегнетоэлектриков) линейно зависит от напряженности внешнего поля.

, где - диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика (положительная безразмерная величина)

21. Электрическое смещение

Напряженность электростатического поля зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна . Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для изотропной среды записывается как

Кл/м². Вектор D описывает электростатическое поле, создаваемое свободными зарядами, но при таком их распределении в пространстве, какое имеется при наличии диэлектрика. Аналогично линиям напряженности можно ввести линии электрического смещения. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь. Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверхность

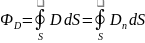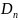, где - проекция вектора D на нормаль n к площадке dS.