3. Колебания. Виды колебаний.

Колебания – движения или процессы в той или иной мере повторяющиеся во времени. Виды: 1) механические – механические движения тела, при которых состояния движения тела повторяются с течением времени (биение сердца); 2) электромагнитные – повторяющиеся изменения электрических и магнитных полей, происходящие в колебательном контуре; 3) смешанные.

4. Затухающие и незатухающие колебания

Затухание колебаний – постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системы. Незатухающие колебания – колебания, амплитуда которых не убывает со временем, а остается постоянной.

5. Дифференциальное уравнение свободных затухающих колебаний и ее решение

. S – колеблющаяся величина. =const – коэффициент затухания, 0 – циклическая частота свободных незатухающих колебаний той же колебательной системы. В случае малых затуханий (²<< ) решение этого уравнения: 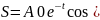, где А=А0 - амплитуда затухающих колебаний, А0 – начальная амплитуда, 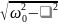= - циклическая частота затухающих колебаний. Затухание нарушает периодичность колебаний. затухающие колебаний не являются периодическими, однако, если затухание мало, то можно условно пользоваться понятием периода затухающих колебаний как промежутка времени между двумя последующими максимумами колебаний фаз величины: Т=2π/=2π/

6. Понятие о коэффициенте затухания, декременте и логарифмическом декременте затухания, времени релаксации и добротности колебательной системы

Коэффициент затухания - =const; Если A(t) и A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение 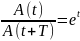, называется декрементом затухания, а его логарифм 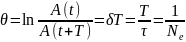- логарифмическим декрементом затухания; - число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания – постоянная величина для данной колебательной системы. Промежуток времени =1/, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации. Для характеристики колебательной системы пользуются понятием добротности Q, которая при малых значениях логарифмического декремента (так как затухание мало ²<< .

7. График затухающих колебаний

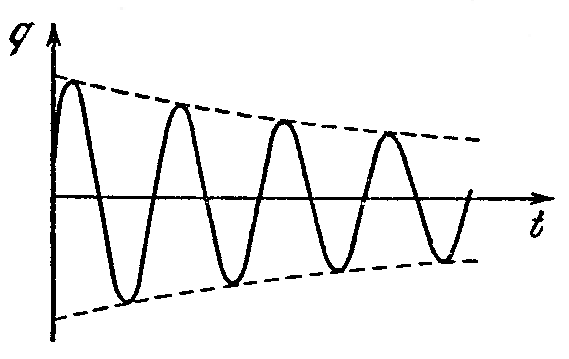
8. Периодические колебания

Периодические колебания – колебания, повторяющиеся через равные промежутки времени.

9. Свободные и вынужденные колебания

Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии, без дальнейшего внешнего воздействия на колебательную систему. Колебания называются вынужденными, если они происходят под действием периодически изменяющейся внешней силой. Для возникновения свободных колебаний необходимо чтобы выполнялось 2 условия: 1) при выведении тела из положения равновесия в системе должна возникнуть сила, направленная к положению равновесия; 2) трение при этом должно быть достаточно малым.

10. Автоколебания

Автоколебания –незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой.

11. Гармонические колебания

Гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса)

12. Дифференциальное уравнение гармонических колебаний и его решение

. Решением этого уравнения является s=Acos(0t+), где А – максимальное значение колеблющейся величины, называемой амплитудой колебания, 0 – круговая (циклическая) частота.

13. График гармонических колебаний

Обычная синусоида

14. Понятие об амплитуде, частоте, фазе и периоде

Амплитуда – максимальное значение колеблющейся величины.

Фаза колебаний – периодически изменяющийся аргумент косинуса (0t+)

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2π, т.е. 0(t+T)+= (0t+)+2π, откуда T=2π/0

Величина, обратная периоду колебаний, =1/Т, т.е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. 0=2π. [] – герц (Гц); 1 Гц – частота периодического процесса, при которой за 1 с совершается один цикл процесса.