1. Электрическое поле, его основные свойства.

ЭП – особый вид материи, не воспринимаемый органами чувств человека и образующийся вокруг электрически заряженных тел/частиц. Основное свойство: силовое воздействие как на движущиеся, так и на неподвижные электрические заряды.

2. Электростатическое поле и его характеристики.

ЭстП – ЭП, характеристики которого не изменяются с течением времени. (источником ЭстП являются неподвижные эл. заряды) Характеристики: 1. Напряженность ЭП Е ( - вектор далее) – силовая характеристика, которая определяет силу, действующую на заряд q в данной точке ЭП со стороны этого поля

Е=Fэп/q В/м; Н/Кл

2. Потенциал  - энергетическая характеристика, определяющую потенциальную энергию произвольного точечного заряда q в данной точке ЭстП

=П/q Дж/Кл; В

3. Графическое изображение электростатического поля: с помощью силовых линий и эквипотенциалей

Силовой линией СЛ называется линия, касательная в каждой точке которой совпадает с направлением вектора Е в этой точке

Принять, что СЛ начинаются на положительных зарядах и заканчиваются на отрицательных; СЛ нигде не пересекаются.

Однородным ЭП называется ЭстП, в каждой точке которой вектор Е имеет одну и ту же величину и направление.

Эквипотенциалью называется геометрическое место точек с одинаковым потенциалом.

С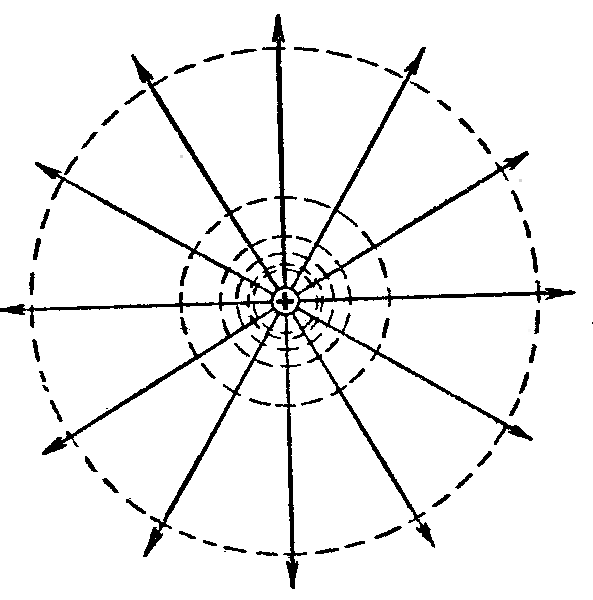 Л всегда перпендикулярны Эквип. СЛ и Эквип для поля точечного заряда:

4. Точечный электрический заряд

Точечным называется заряд, размерами которого в условиях данной задачи можно пренебречь. 1. Напряженность ; 2. Потенциал

5. Закон Кулона

Позволяет определить силу электростатического взаимодействия двух точечных зарядов

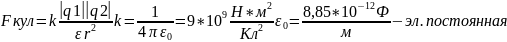
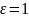; , вакуум и воздух

6. Принцип суперпозиции для электростатических полей

Позволяет определить E и системы точечных зарядов

Напряженность поля системы зарядов равна векторной сумме напряженности полей, которые создавал бы каждый из зарядов системы в отдельности. Ерез=Е1+Е2+Еi=Еi; рез=1+2+i=i

7. Потенциальная энергия электростатического взаимодействия двух точечных зарядов, системы точечных зарядов.

- 2 точечных зарядов

- системы точечных зарядов. - потенциал в точке, где находился заряд qi, создаваемый всеми зарядами системы, кроме 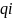. Находится по принципу суперпозиции.

8. Работа электростатического поля по перемещению точечного заряда.

А=Fэп S cos α; A=-(П2-П1); А=q(1-2)

Работа, совершаемая силой F при перемещении заряда q0 на отрезок dl:

dA=Fdlcos(F, dl)= q0E cos(F, dl) dl

В случае конечного перемещения заряда q0 из точки а в точку в

, Edl - скалярное произведение векторов.

9. Циркуляция вектора Е электростатического поля

работа по перемещению заряда q0 из точки 1 в точку 2

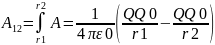. Из этого следует, что работа, совершаемая при перемещении электрического заряда по любому замкнутому пути L, равна 0, т.е. . Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути dl равна Е dl = El dl, где El = Ecosa — проекция вектора Е на направление элементарного перемещения. Тогда формулу можно записать в виде .(1) Этот интеграл называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (1) , называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.