6.3. Работа №3. «Обоснование теоретического закона

распределения случайных характеристик транспортного

процесса»

Бланк задания приведен ниже

Задание №3

на лабораторную работу по дисциплине

«Исследование систем управления»

Тема: «Обоснование теоретического закона распределения

случайных характеристик транспортного процесса»

Постановка задачи. В результате наблюдений зафиксированы нижеприведенные значения ___________________________________________

Выровнять приведенные статические данные с помощью теоретического закона распределения случайных величин.

Исходные данные ________________________________________________________________

________________________________________________________________

Методика выполнения задания

Под выравниванием (сглаживанием) понимается определение для множества дискретных точек определенной закономерности. Транспортный процесс в силу влияния множества факторов носит вероятностный характер, поэтому параметры его характеризуются случайными величинами. Элементы неопределенности, присущие случайным величинам, требуют создания специальных вероятностных методов исследований. Практика показывает, что, наблюдая в совокупности массы однородных случайных явлений, можно обнаружить в них вполне определенные закономерности. Использование этих закономерностей в практической деятельности позволяет предсказать средний исход массы аналогичных опытов и достигать, таким образом, эффективного управления.

Понятие закона распределения случайных величин

Транспортный процесс, и не только он, характеризуется непрерывными и дискретными случайными величинами.

Непрерывной случайной величиной называется та, значения которой непрерывно располагаются в некоторых пределах (масса и рост человека, размер ступни, затраты времени на выполнение какой-либо операции, интервалы поступления заявок оператору мобильной связи и т.п.).

Случайная величина называется дискретной, если она принимает конечное, счетное значение (число пассажиров в автобусе, число контейнеров, отправленных 31 мая из Нижегородского порта, число судов, прибывших в августе к Городецким шлюзам и т.п.).

Не имея возможности предсказать точное значение любой случайной величины, можно определить границы изменения или вероятность принятия ею определенного значения из ряда возможных. Таким образом, вероятность есть численная мера степени возможности какого либо события.

Законом распределения случайной величины называют соотношение, устанавливающее связь между возможными значениями ее и соответствующими им вероятностями.

На практике используются четыре формы законов распределения случайных величин.

Ряд распределения. Пример. За 18 суток июля из Нижегородского порта назначением на Волгоград был отправлен 601 контейнер, в т.ч. по датам: 01.07-27; 02.07-39; 03.07-27; 04.07-40; 05.07-35; 06.07-27; 07.07-37; 08.07-35; 09.07-364 10.07-25; 11.07-33; 13.07-374 14.07-33; 15.07-33; 16.07-36; 17.07-37; 18.07-31.

Построить ряд распределения.

Ряд распределения строится в табличной форме (см. табл. 9).

В примере оценивается вероятность появления события, например, отправления 27 (трижды из 18 суток) или 39 (один раз) контейнеров.

Из примера следует два важных вывода:

На практике с целью выполнения последнего требования «невязку» или вычитают или прибавляют к разряду с максимальным числом наблюдений.

Таблица 9

Ряд распределения

Число дней	3	1	1	2	3	4	1	1	2
Число отправленных контейнеров	27	39	40	35	37	33	25	31	36
Статистическая вероятность	0,167	0,056	0,058	0,111	0,167	0,220	0,056	0,056	0,111

Многоугольник (гистограмма) – это графическая интерпретация функции

Знак «*» указывает на то, что вероятность определена из статистических данных.

Функция распределения – есть вероятность того, что значение случайной величины окажется меньше значения некой текущей переменной.

, где Х – случайная величина, х – текущая переменная.

Графическая интерпретации функции распределения сводится к тому, что при перемещении на числовой оси случайных величин Х текущей переменной х вправо увеличивается зона распределения вероятностей.

Для нашего примера если 0< х <25, то , т.к. меньше 25 контейнеров не отправлялось. Если , то было одно событие и , если , то было уже четыре события (одно отправление 25, и три отправления 27 контейнеров) и = 0,223 = 0,056 + 0,167.

Функцию распределения строят в осях: – ось ординат и текущая переменная – ось абсцисс.

Ряд, многоугольник и функция распределения являются универсальными законами, т. е описывают и дискретные, и непрерывные случайные величины.

Кроме того, для непрерывных случайных величин (они дифференцируемы на всём диапазоне изменения значений) в качестве закона используется плотность распределения случайной величины, являющаяся первой производной функции распределения. Плотность распределения обозначается

Теоретические законы распределения непрерывных

случайных величины. Нормальный закон (закон Гаусса)

Этот закон наиболее часто используют в практике исследований, т.к. им описывается большинство разнообразных явлений.

Плотность распределения вероятностей (вероятность, приходящаяся на единицу времени, массы, площади и т.д.) выражается формулой

,

(80)

где – значение i–й случайной величины; – математическое ожидание; – среднее квадратное отклонение; , – константы.

В расчётах принимать =3,1416, =2,7182.

Кривая плотности распределения вероятностей симметрична относительно математического ожидания (рис. 4).

Для нормального закона характерны две особенности:

– малые значения коэффициента вариации ;

– практически все отклонения от математического ожидания заключены в интервале , а вероятность попадания случайной величины в разные интервалы характеризуется данными:

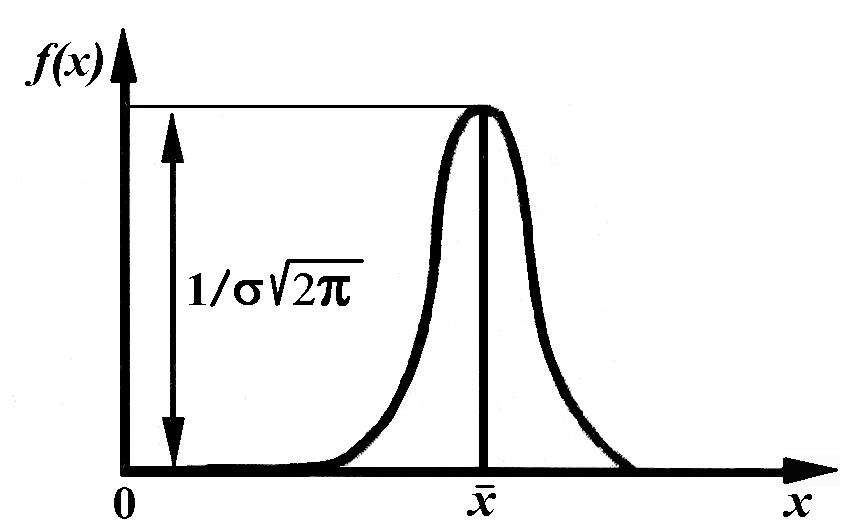
Рис. 4. Вид кривой плотности нормального распределения

Значение максимальной ординаты определяется выражением

.

Указанные особенности используются для распознавания закона при обработке статистических данных.

Закон Эрланга (нормированное распределение)

Закон описывает большое число операций транспортного процесса и характеризуется двумя параметрами: ; .

Функция плотности распределения определяется по выражению

.

(81)

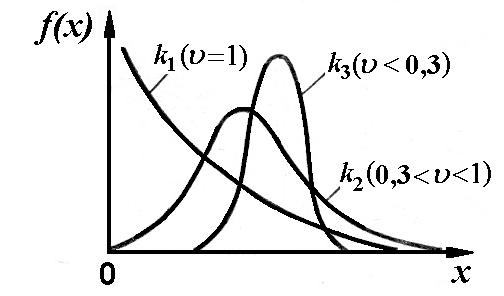
На рис. 5 приведена функция плотности распределения при k₁  k₂  k₃.

Рис. 5. Функция плотности распределения закона Эрланга

Из рисунка следует, что закон Эрланга описывает операции в значительных пределах:

– при 0 – регулярный процесс, совершаемый через равные промежутки;

– 1 – совершенно случайный процесс с большими отклонениями от среднего значения;

– при 0    1 – регулируемый процесс, в котором прослеживаются усилия аппарата управления, однако наблюдаются некоторые отклонения от средних или плановых значений.

Ориентиром для выбора этого закона является значение коэффициента вариации.

Показательный (экспоненциальный) закон

Этот закон является частным случаем закона Эрланга при k = 1. законом описываются различные технологические ожидания. Уравнение плотности распределения имеет вид

(82)

Кривая плотности распределения приведена на рис. 5 для k₁

Особенностью закона является равенство среднего значения и среднего квадратического отклонения

(83)

Для дискретных случайных величин имеются свои собственные законы распределения: закон Пуассона, биноминальное и геометрическое распределения, которые используются в практике исследований транспортных процессов. Особенности использования этих законов изучаются в специальной литературе.

Сглаживание статистических данных с помощью теоретического закона распределения случайных величин

В этом разделе излагается непосредственно методика выполнения третьей работы в последовательности и объеме следующих пунктов.

1. В ходе наблюдений случайные величины фиксируются в протоколе, где указывается номер опыта k и значение случайной величины x_k в этом опыте, по форме табл. 10.

Таблица 10

Протокол наблюдения

k

xk

k

xk

k

xk

При выполнении статистических исследований для практических целей важным является вопрос о необходимом числе данных. Для операций, обладающих значительной устойчивостью число данных должно быть в пределах 100–400, для неустойчивых – до 2000.

2. Первым шагом для осмысливания статистики является упорядочивание ее в порядке возрастания или убывания. Эта процедура позволяет определить диапазон изменения значений случайной величины и упрощает подходы к обработке массива. Упорядочивание выполняется по форме табл. 11, при этом повторяющиеся значения располагаются подряд под разными номерами.

Таблица 11

Упорядоченная статистическая совокупность

i

xi

i

xi

i

xi

Табл. 11 должна содержать одинаковое с табл. 10 число данных.

3. По данным табл. 11 выполняются расчеты значений функции распределения .

Пример. Пусть имеется упорядоченная статистическая совокупность размером n = 54. значения i и x_i, ч характеризуется следующим: 1–75; 2–80; 3–82; 4–82; 5–85; 6–87; 7–87; 8–91; …. Тогда при х  75 F(x) = 0; при 75  х  80 F(x) = 1/54 = 0,0185; при 75  х  82 F(x) = 0,019 + 1/54 = 2/54 = 0,037; при 75  х  85 F(x) = 0,037 + 2/54 = =4/54 = 0,0740 и т.д.

Результаты расчета сводятся в таблицу (см. табл. 12).

Таблица 12

Значения функции распределения

х, ч	F*(x)	х, ч	F*(x)
х  75	0
75  х  80	0,0185
75  х  82	0,0370
75  х  85	0,0740
75  х  87	0,0926
75  х  91	0,1296
…	…

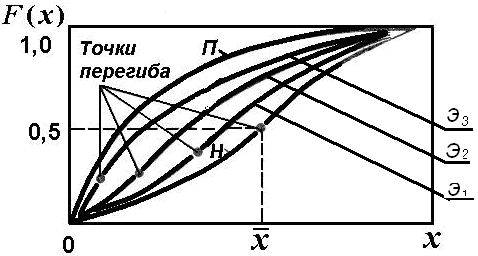
По информации табл. 12 строится на миллиметровке формата А4 график функции распределения в осях: ось ординат – значение F(х); ось абсцисс – текущая переменная х. Он будет иметь ступенчатую форму, т.к. в точках 75, 80, 82… происходит количественное изменение значений F(х). Однако с увеличением числа опытов ступенчатость будет стремиться к плавной кривой. По виду статистического графика F(х), сравнивая его со стандартными распределениями теоретических законов (см. рис. 6), принимается первая гипотеза о законе распределения исследуемой статистической совокупности.

На рис. 6 график Э₁, соответствует кривой k_3, Э₂ – k₂ и Э₃ – k₁ рис. 5.

4. Обоснование второй гипотезы о теоретическом законе.

Для этого формируется группированный статический ряд по форме табл. 13.

Рис. 6. Функция распределения для нормального (Н),

эрланговского (Э) и показательного (П) законов

Весь участок оси абсцисс, на котором расположены значения случайных величин X_i, делится на участки (разряды). Число разрядов определяется по эмпирическому выражению

(84)

с округлением до целого числа по правилам математики. Оптимальная величина интервала (шаг разряда) определяется по формуле

(85)

с округлением таким образом, чтобы величина выражалась «круглыми» числами (3,0 или 2,3).

За начало первого интервала принимается значение, равное a₁ = x_min – h  2, начало второго интервала – a₂ = a₁ + h, третьего – a₃ = a₂ + h и так до тех пор, пока начало следующего по порядку интервала не будет равным или большим х_maх. Подобный прием позволяет применительно к исследуемому статическому ряду выявить наиболее характерные его черты.

После этого на базе данных табл. 11 определяется число случайных величин, попавших в тот или иной разряд. Если значение случайной величины совпало со значением границы разряда, то рекомендуется использовать «симметричное» правило, в соответствии с которым половина относится к левому, а другая – к правому разряду. Например, установлены границы разрядов 70 и 80 ч. Тогда, применительно к фрагменту статистического ряда из п.3. настоящей методики в разряд 70–80 попадает 1,5 случайных величин (одна – это значение 75 ч, 0,5 – это половинка второй случайной величины – 80 ч).

Плотность вероятности определяется отношением вероятности к шагу разряда. Результаты сводятся в табл. 13.

Таблица 13

Группированный статический ряд

разряды	70–80	80–90	…
Число случайных величин, попавших в разряд с учетом половинок	1,5		…
Число опытов (наблюдений)	54
Статистические вероятности	0, 028		…
Статистические плотности вероятностей	0, 0028		…

По данным табл. 13 строится гистограмма на листе миллиметровке формата А4 в осях: ось ординат – значение плотности; ось абсцисс – случайные величины с указанием границ разрядов. Границы разрядов являются основаниями прямоугольников, высота которых определяется значениями плотности. Полученная фигура называется гистограммой, является дискретным отражением статистической плотности вероятностей и характеризует в определенной мере существенные черты исследуемого ряда. Для повышения адекватности производится сглаживание гистограммы плавной кривой (график статистической плотности) таким образом, чтобы площадь гистограммы и площадь под кривой статистической плотности были равны. Сравнивая полученную кривую с кривыми рис. 4 и 5 принимаем вторую гипотезу о теоретическом законе распределения исследуемого статистического ряда.

5. Обоснование третей гипотезы о теоретическом законе.

С этой целью определяются дисперсионные характеристики статического ряда. Методика расчета рассматривается в первой работе (формулы (55), (56), (57)). По численному значению коэффициента вариации с учетов выше изложенных особенностей теоретических законов принимается третья гипотеза о законе распределения.

6. Построение теоретической кривой плотности вероятностей.

Значение точек, лежащих на теоретической кривой плотности, характеризующей исследуемый статистический ряд, определяется подстановкой вместо х_i значения границ разрядов в формулы (80), (81) или (82). Выбор той или иной формулы определяется принятой гипотезой. Точность расчетов – 7–8 знаков после запятой, при этом для нормального закона определяется максимальное значение ординаты по формуле Результаты расчетов сводятся в таблицу (см. табл. 14).

Таблица 14

Значение точек, лежащих на теоретической кривой

плотности вероятностей

Границы разрядов	70	80	90	…
Значение плотности f(x)

Точки наносятся на рисунок с гистограммой, соединяются плавной кривой теоретического закона, которая выровняла исследуемый статический ряд случайных величин.

7. Проверка гипотезы по критериям согласия.

Критерий согласия дает численную меру сходимости статического и подобранного для него теоретического распределений. В качестве критериев согласия используются критерии Колмогорова, Пирсона, Фишера, Стьюдента, Романовского, Ястремского. Мы познакомимся с наиболее простыми в вычислительном отношении критериями.

Критерий Пирсона

Механизм проверки сходимости распределений построен на сравнении статистического и теоретического значений критерия.

Статистическое значение критерия Пирсона (зачастую используется термин «критерий хи квадрат») определяется по формуле

(86)

где j – признак разряда (колонки в табл. 13); m_j^* – статистическое число случайных величин в j-м разряде (принимается по данным табл. 13); n – число опытов (статистических данных); P_j – теоретическая вероятность попадания случайной величины в j-й разряд; m_j – теоретическое число случайных величин в j-м разряде.

mi = f (x)h n.

(87)

Подготовительный этап для расчета статистического значения критерия рекомендуется оформить в табличной форме (см. табл. 15).

Значения f(x) и m_j^* принимаются соответственно из табл. 14 и 13. При переносе данных в табл. 15 правое или левое (минимальное из них) значение нужно исключить.

Теоретическое значение критерия приведено в приложении. Оно зависит от двух параметров:

r – число степеней свободы;

p – уровень значимости, определяющий область критических отклонений теоретического распределения в размере p = 0,01–0,05.

Таблица 15

Расчет теоретического числа случайных точек

Разряды	70–80	80–90	…
Число опытов (n)
Шаг разряда (h)
Значение плотности (f(x))			…
Статистическое число случайных величин в разряде (mj*)			…
Теоретическое число случайных величин в разряде (mj)			…

Схема определения теоретического значения критерия сводится к следующему.

1. Определяется число степеней свободы.

(88)

где k – число разрядов (колонок в табл. 13); s – число независимых условий (связей), накладываемых на распределения.

В качестве независимых условий используются следующие:

(89)

Могут накладываться и дополнительные условия.

2. Задаются уровнем значимости в пределах p = 0,01–0,05;

3. По приложению или справочникам определяется теоретическое значение χ ².

Гипотеза о принятом теоретическом законе считается не противоречащей опытным данным, если χ ^2*< χ².

Критерий Романовского (Rо)

Гипотеза считается приемлемой, если выполняется условие

(90)

Критерий Ястремского (Js)

(91)

Если условие (91) выполняется, то гипотеза подтверждается.

При выполнении работы необходимо проводить проверку по трем критериям с выводом после расчета каждого критерия. В конце работы приводится обобщенный вывод.

В практической деятельности, если гипотеза не прошла проверку критериями согласия, необходимо исследовать другой теоретический закон.