Индексы переменного, постоянного состава, структуры и их применение в экономическом анализе
В экономическом анализе динамики общественно-экономических явлений используют индексы переменного, постоянного составов и структуры.
Индекс переменного состава отражает динамику средней величины изучаемого признака по совокупности. Его формула такова:
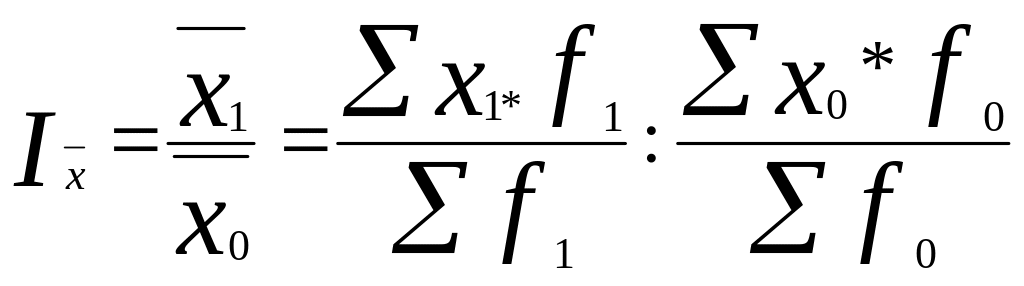, (7.25)
Где:
-
среднее значение признака по совокупности
в отчетном периоде,
- среднее значение
признака по совокупности в базисном
периоде,
- значение признака у единицы совокупности в отчетном периоде,
-
значение признака у единицы совокупности
в базисном периоде,
-
число единиц совокупности в отчетном
периоде,
-
число единиц совокупности в базисном
периоде.
Индекс постоянного состава отражает динамику значения признака под влиянием изменения только значений признака при неизменной структуре. Его формула такова:
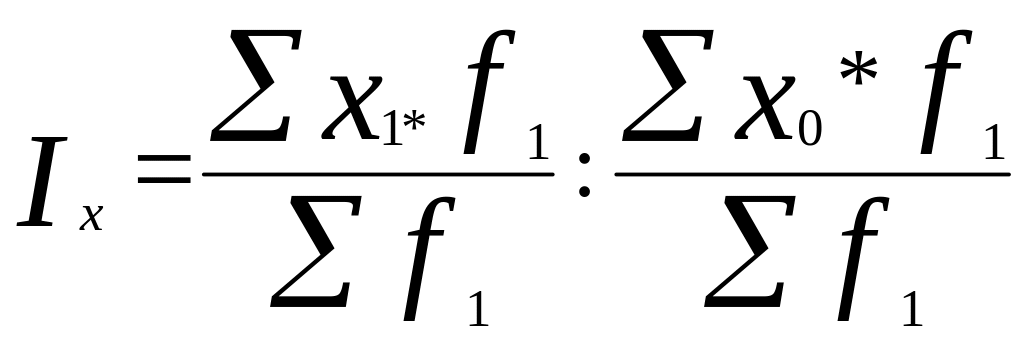. (7.26)
Индекс структуры отражает динамику структуры при неизменном значении признака, принятом на базисном уровне:
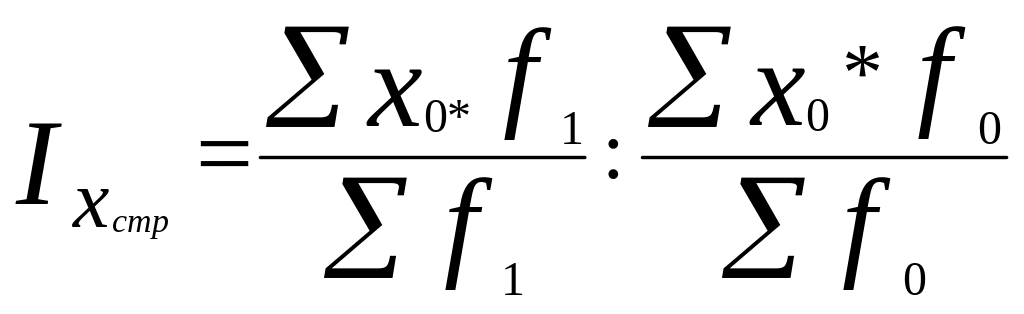. (7.27)
Произведение индексов постоянного состава и структуры равен индексу переменного состава.
*
. (7.28)
Свойства общих индексов
1. Индекс двух индексируемых величин равен произведению индексов этих величин. Например, индекс стоимости всей продукции равен произведению индексов физического объема продукции и индекса цены единицы продукции:
=
,
. (7.29)
2. Базисный индекс величины равен произведению последовательных цепных индексов этой величины с однородным соизмерителем.
Разность между числителем и знаменателем индекса отражает абсолютную динамику совокупности
, (7.30)
(7.31)
- отражает абсолютную
динамику стоимости всей продукции с
учетом изменения объема продукции и
цены единицы продукции,
(7.32)
- отражает
абсолютную динамику стоимости всей
продукции с учетом изменения только
объема продукции,
(7.33)
- отражает абсолютную динамику стоимости всей продукции с учетом изменения только цены единицы продукции. Следовательно, разности между числителем и знаменателем общих индексов отдельных величин (соизмерителей в общем индексе с двумя индексируемыми величинами) отражают абсолютную динамику явления под влиянием отдельных соответствующих факторов.
Тема 10. Выборочное наблюдение
Понятие выборочного наблюдения
Выборочным наблюдением называется несплошное наблюдение, при котором отбор подлежащих обследованию единиц изучаемого явления организуется по принципу случайного отбора по теории вероятности.
При случайном отборе каждой единице изучаемого явления обеспечивается определенная (обычно равная) вероятность попасть в количество обследуемых единиц. Этим исключается односторонность подбора единиц. Строгое соблюдение правил выборочно наблюдения обеспечивает близкое соответствие состава охваченной наблюдением массы и состава всей массы единиц изучаемого явления.
Выборочное наблюдение по сравнению со сплошным требует меньше затрат времени и обеспечивает более глубокое исследование явления. По выборочным данным можно не только приближенно определить различные показатели изучаемого явления, но и рассчитать пределы возможной ошибки выборочного наблюдения.
Характеристики генеральной и выборочной совокупности
генеральной совокупностью называется вся совокупность единиц, из которой производится отбор.
Выборочной совокупностью называется совокупность единиц, отобранных для выборочного наблюдения.
Средняя величина
и дисперсия изучаемого
признака в генеральной совокупности
называются генеральная
средняя и генеральная дисперсия.
Они обозначаются соответственно
и
.
В выборочной
совокупности они называются выборочной
средней и выборочной дисперсией
соответственно и обозначаются:
и
.
Число единиц, образующих генеральную совокупность, обозначается через N. Число единиц в данной совокупности, обладающих изучаемым признаком, - М, а число единиц, не обладающих этим признаком – N-M.
Доля единиц в генеральной совокупности, обладающих изучаемым признаком, называется генеральной долей или просто долей и обозначается Р.
Р=М:N. (10.1)
Доля единиц, не обладающих этим признаком, обозначается
g = (N-M):N. (10.2)
Число единиц в выборочной совокупности, обладающих изучаемым признаком, называется частотой и обозначается буквой m, а численность всех единиц выборочной совокупности обозначается буквой n.
Доля единиц выборочной совокупности, обладающих изучаемым признаком, называется частостью и обозначается буквой w:
W=m:n. (10.3)
Одни и те же показатели выборочной и генеральной совокупностей не совпадают по величине, т.е. могут быть разными.