
- •Содержание
- •1 Лекция
- •1.1 Дифференциальный усилитель
- •1.2 Операционный усилитель
- •2 Лекция
- •2.1 Идеальный оу
- •2.2 Инвертирующий и неинвертирующий масштабные усилители
- •2.3 Дифференциальные усилители на оу
- •2.4 Усилители тока и усилители с токовым выходом
- •2.5 Преобразователи сопротивления в напряжение
- •3 Лекция
- •3.1 Линейные частотно–зависимые схемы на оу
- •3.4 Активные фильтры
- •4 Лекция
- •4.1 Применения оу в нелинейных цепях
- •4.2 Прецизионные выпрямители
- •4.3 Фазочувствительные выпрямители
- •4.5 Амплитудные ограничители
- •5 Лекция
- •6 Лекция
- •7 Лекция
- •8 Лекция
- •9 Лекция
- •Список литературы
- •050013, Алматы, Байтурсынова, 126
3.4 Активные фильтры
Фильтр – это такая схема, которая пропускает сигналы одних частот и не пропускает сигналы других частот. Основными типами фильтров являются фильтр нижних частот (ФНЧ), фильтр верхних частот (ФВЧ), режекторный фильтр (РФ) и полосовой фильтр (ПФ).
а)
 б)
б)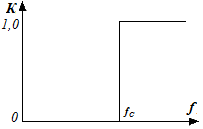
в)
 г)
г)
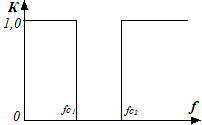
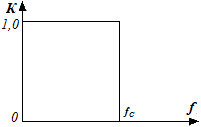
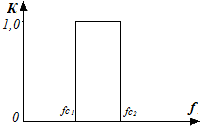
Рисунок 15 – Частотные характеристики идеальных фильтров:
ФНЧ – а), ФВЧ – б), ПФ – в), РФ – г).
Амплитудно-частотные характеристики (АЧХ) идеальных фильтров изображены на рис. 15. Так, идеальный ФНЧ пропускает все частоты от постоянного тока до частоты среза fc, т.е. в полосе пропускания 0... fc коэффициент пропускания К равен единице, а в полосе задерживания К = 0. Идеальный ФВЧ наоборот, пропускает сигналы с частотами выше fc, но подавляет полностью частоты от 0 до fc.
Идеальный ПФ пропускает сигналы в полосе частот от fc1 до fc2, подавляя сигналы, частоты которых находятся ниже и выше полосы пропускания. Идеальный режекторный фильтр напротив, в полосе частот fc1 ... fc2,
задерживает сигналы и пропускает сигналы с частотами вне полосы задерживания.
Идеальные фильтры физически реализовать невозможно, реальные ARC-фильтры строят из ОУ и пассивных элементов – резисторов и конденсаторов. Так, в качестве простейшего ФНЧ можно использовать интегратор, а дифференциатор может служить простейшим ФВЧ. Для обеих схем частоты среза определяются выражением
fc = 1/2πROCC. (3.3)
Оба фильтра называются фильтрами первого порядка, поскольку тот и другой имеют по одной RC – цепочке.
Однако такого типа фильтры имеют слишком малую крутизну АЧХ в области частоты среза, а именно 20дб/дек, на практике обычно требуются более высокие крутизны, то есть требуется более тесное приближение реальных АЧХ к идеальным.
В математике известны различные формулы, аппроксимирующие идеальные АЧХ. Все эти выражения: Баттерворта, Чебышева, Бесселя, эллиптическое и др. представляют собой отношение двух операторных полиномов. Аппроксимация характеристик ARC-фильтров сводится к выбору таких коэффициентов этих полиномов, которые обеспечивают наилучшее приближение к желаемым АЧХ или ФЧХ фильтра.

Рисунок 16 – Графики АЧХ активных фильтров нижних частот четвёртого порядка.
На рис. 16 показаны графики АЧХ активного ФНЧ чевёртого порядка для различных аппроксимаций, здесь же присутствует и характеристика идеального фильтра. Из рисунка видно, что наибольшую скорость спада АЧХ в переходной области (между полосами пропускания и заграждения) имеет эллиптический фильтр – кривая 1. Далее следует фильтр Чебышева –
кривая 2 и Баттерворта – кривая 3. Наихудшим в этом смысле является фильтр Бесселя – кривая 4. Однако при скачке входного сигнала выходное напряжение фильтра Бесселя устанавливается наиболее быстро, а у эллиптического фильтра и фильтра Чебышева – наиболее медленно.
К настоящему времени разработано множество методик синтеза ARC-фильтров. Так, в (3) описан сравнительно простой вариант расчёта фильтров от второго до шестого порядка по Бесселю, по Чебышеву и по Баттерворту с единичным коэффициентом передачи в полосе пропускания с неравномерностью АЧХ в 1дБ. При необходимости построения фильтров более высокого порядка следует соединить каскадно несколько фильтров.
Схемотехника ARC-фильтров основана на использовании базовых структур с инвертирующим и неинвертирующим включением ОУ, см рис. 17.
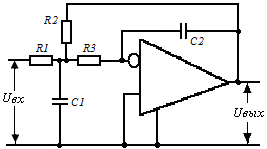
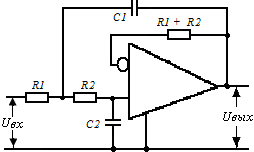
а) б)
Рисунок 17 – Схемы базовых структур ARC-фильтров второго порядка:
схема Рауха – а), схема Саллена-Ки – б).
Фильтры второго порядка, пропускающие верхние частоты, легко получить из соответствующих фильтров нижних частот. Для этого в схеме рис. 17- а резисторы R1, R2, R3 заменяются конденсаторами, а конденсаторы С1, С2 – резисторами. В схеме рис. 17- б аналогично резисторы R1, R2 заменяются на конденсаторы, а конденсаторы С1, С2 – на резисторы.
Что касается полосовых и режекторных фильтров, то их можно построить, комбинируя соответствующим образом фильтрв нижних и верхних частот. ARC-фильтры находят широкое применение в измерительной технике для обработки аналоговых сигналов.
