Характер процессов системы

Характер переходного процесса определяется (характеристическое уравнение разомкнутой системы).

Устойчивость – способность системы возвращаться к состоянию устойчивого равновесия после снятия причин, вызвавших отклонение системы от состояния устойчивого равновесия.

При действии на систему возмущений применим метод суперпозиций (наложения).

Система автоматического управления:

1. Устойчива, если ;

2. Неустойчива, если ;

3. На границе устойчивости, если .

Если линейная система устойчива, то она устойчива в целом, то есть при любых возмущениях.

Если нелинейная система устойчива, то может быть устойчива в малом и большом отношении.

Корни характеристического уравнения могут быть

1. 

2. 

3. 

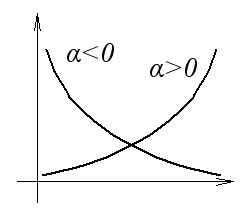
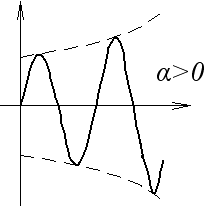
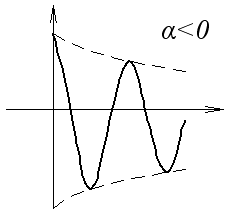
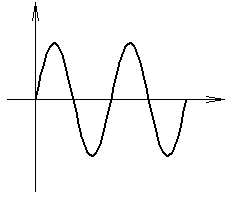
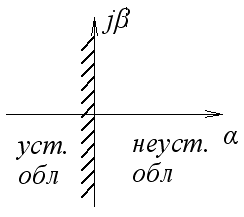
Система будет на границе устойчивости, если среди корней есть либо один нулевой, либо пара мнимых, а все остальные – левые.

1. Система неустойчива, так как есть правый корень.

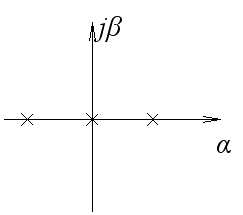
2. Система неопределенная.

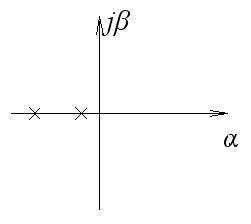
3. Система устойчива.

Критерий устойчивости (правило, позволяющее определить характер системы, не вычисляя корень).

Различают алгебраический и частотный критерии устойчивости.

Алгебраические критерии: критерий Гаусса и критерий Гурвица.

Частотные критерии: критерий Михайлова, критерий Найквиста, метод D-разбиений и метод корневого годографа.

Рассмотрим критерий Гаусса.

Необходимо знать либо характеристическое уравнение, либо передаточную функцию.

Система будет устойчивой, если все коэффициенты первого столбца будут больше нуля.

В характеристическом уравнении число правых корней равно числу смен знаков коэффициентов первого столбца.

– наиболее возможное при заданных параметрах значение коэффициента, при котором замкнутая система становится на границе устойчивости.

Разомкнутая система устойчива.

Судя по коэффициентам первого столбца, замкнутая система неустойчива, в характеристическом уравнении два правых корня.

Критерий Гурвица

Из коэффициентов характеристического уравнения составляется таблица из n-строк и n-столбцов.

						…
						…
	0					…
	0					…
	0	0				…
	…	…	…	…	…	…

Система автоматического управления устойчива, если и все .

Устойчивость разомкнутой и замкнутой системы.

Разомкнутая система устойчива.

Замкнутая система неустойчива.

		0
		0
0