5.2. Контрольные вопросы

1. Назовите причины вибрации ГТД при работе?

2. Дайте определение коэффициенту вибрационной перегрузки.

3. Какими параметрами определяется виброперегрузка двигателя?

4. Методы определения и снижения виброперегруки двигателя.

5. Что такое статическая балансировка роторов?

6. Что такое динамическая балансировка роторов?

7. Дайте определение дисбаланса.

6. Расчёт на прочность дисков роторов гтд

Диски роторов ГТД, работают при высоких скоростях вращения, при высоких температурах (газовые турбины) и её градиенте вдоль радиуса, что обуславливает появления в них значительных нагрузок.

На рабочем установившемся режиме в диске возникают следующие напряжения:

- напряжения растяжения от центробежных сил самого диска, а также от центробежных сил масс лопаток установленных на ободе диска;

- температурные напряжения, обусловленные изменением температуры, как по радиусу, так и по толщине;

- напряжения изгиба от газовых сил, действующих на лопатки от газовых сил, а также от центробежных сил масс лопаток и диска в случае отклонения центров тяжести этих масс от срединной плоскости диска.

Кроме того, из-за высоких температур, снижается механическая прочность материала диска.

Существует два основных подхода к расчёту дисков на прочность:

1. Анализ прочности диска известного профиля.

2. Определение оптимального профиля диска с учетом ограничений на его характеристики прочности.

По первому подходу проверяются его прочностные свойства по двум критериям:

- по запасу прочности;

- по несущей способности (разрушающим оборотам).

При невыполнении одного из двух критериев необходимо изменять геометрию диска или применять другой материал.

По второму подходу для выполнения расчетов необходимы пакеты программ и уточнение профиля диска по конструктивным соображениям.

Расчёт прочности диска связан с определением напряжённого состояния в любой точке диска и для диска любой конструктивной схемы является очень сложной задачей.

Рассмотрим упрощенную расчетную схему по определению напряжений в диске.

Примем следующие допущения:

- материал диска упругий;

- диск тонкий (толщина диска много меньше наружного радиуса);

- диск симметричен относительно своей срединной плоскости;

- напряжения изгиба и кручения не учитываются;

- температура изменяется только по радиусу;

- напряжения от лопаток на внешнем диаметре и от запрессовки диска на вал распределены равномерно по толщине и окружности.

С учётом допущений можно считать, что в диске возникают напряжения направленные по нормалям к кольцевому сечению и радиальному сечению диска.

Исходными для расчета напряжений в диске являются уравнения равновесия и уравнения совместных деформаций, выраженные в напряжениях.

Уравнения равновесия. Рассмотрим условия равновесия сил действующих на бесконечно малый элемент диска заключенный между двумя концентрическими поверхностями, отстоящими на расстоянии друг от друга и на расстоянии от оси вращения и двумя радиальными поверхностями, проходящими через ось вращения под углом (рис.6.1).

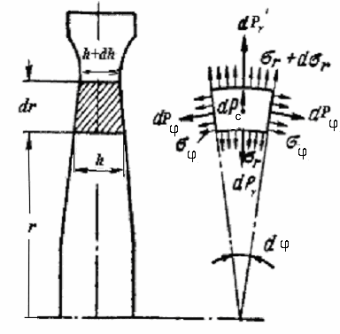
Рис. 6.1. Расчетная схема диска на прочность от центробежных сил

При вращении диска угловой скоростью на выделенный элемент действует центробежная сила , приложенная в центре тяжести, которая определяется по зависимости

(6. 1)

где - масса выделенного элемента; составляющими порядка и др. пренебрегаем ввиду их малости

От действия центробежной силы на концентрических и радиальных поверхностях выделенного элемента возникают нормальные напряжения:

- на внутреннем цилиндрическом сечении, расположенном на радиусе напряжение , и радиальная сила, направленная к центру вращения ;

- на внешнем цилиндрическом сечении, расположенном на радиусе напряжение и радиальная сила, направленная от центра вращения ;

- на радиальных поверхностях, ввиду симметричности элемента тангенциальные напряжения на обеих гранях равны и также как и силы направлены по нормали к поверхности.

Составим уравнения сил на поверхностях выделенного элемента от нормальных напряжений.

На внутренней цилиндрической поверхности

(6.2)

На внешней цилиндрической поверхности

(6.3)

На радиальных поверхностях

(6.4)

Спроецируем все силы на вертикальную ось и запишем уравнение равновесия сил действующих на выделенный элемент

. (6.5)

Подставляя выражения (6.1 … 6.4) и учитывая, что ввиду малости получим уравнение равновесия в напряжениях

(6.6)

В уравнении (5.6) при известном законе изменения толщины диска по радиусу содержится два неизвестных .

Второе уравнения получим, связав с деформациями по закону Гука с учетом температурных деформаций. Относительные удлинения волокон в радиальном и окружном направлениях определятся

, (6.7)

где -коэффициент Пуассона; - коэффициент температурного линейного расширения материала диска; - температура диска на радиусе .

Относительные удлинения и связаны с удлинениями в радиальном и окружном направлениях соотношениями

, (6.8) или (6.9)

Дифференцируя соотношение (6.9), получим

(6.10)

С учетом (6.7) уравнение (6.10) запишется

(6.11)

Подставим в уравнение (6.11) выражения для и , получим

(6.12)

Уравнения (6.6) и (6.12) позволяют найти искомые напряжения и их изменения по радиусу. Точное решение этих уравнений возможно только для частных случаев профилей дисков, например диск постоянной толщины, конический или параболический закон изменения профиля диска по радиусу, диск равного сопротивления (Рис. 6.2).

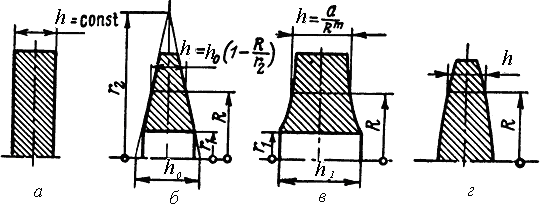
Рис.6.2. Формы профилей дисков: а – постоянной толщины; б -конический; в – гиперболический; г– равного сопротивления

Если нет аналитической зависимости изменения толщины диска по радиусу, то задача решается приближёнными методами.

6.1. РАСЧЕТ ДИСКА ПОСТОЯННОЙ ТОЛЩИНЫ

Для диска постоянной толщины h= const.

Запишем выражение (6.6) с учетом h= const в следующем виде:

( 6.13)

Дифференцируя, по r найдем

(6.14)

Подставим выражения 6.13 и 6.14 в формулу 6.12 получим

(6.15)

Проинтегрируем выражение (6.15) дважды, получим

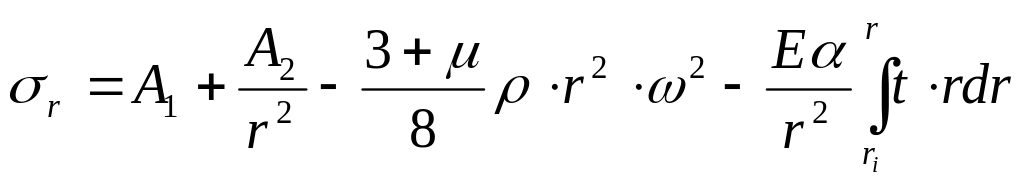, (6.16)

где А₁ и А₂ – постоянные интегрирования; r_i – внутренний радиус диска ( для диска сплошного, без центрального отверстия r_i =0).

Напряжения определяются по формуле (6.13) с учётом выражения (6.16):

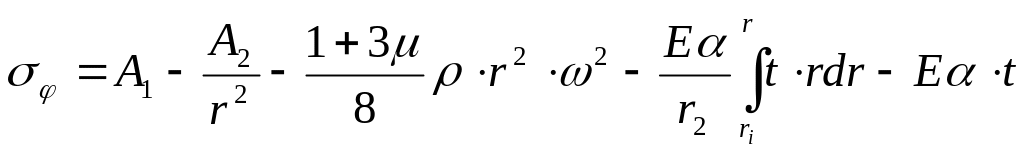( 6.17)

Постоянные А₁ и А₂ определяются из граничных условий. На наружном радиусе диска радиальные напряжения равно нулю при отсутствии лопаток или напряжению от центробежной силы масс лопаток при их наличии.

В сплошном диске r=0, А₂=0 радиальные напряжения равны тангенциальным (см. рис. 6.3,а).

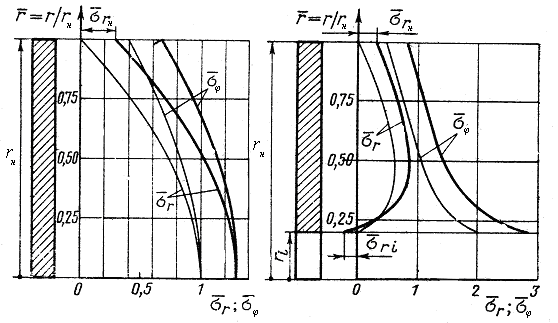а б

Рис. 6.3. Распределения напряжений по радиусу равномерно нагретого вращающегося диска: а - диск сплошной; б - диск с отверстием; ;

В диске с внутренним отверстием радиальные напряжения на контуре свободного ненагруженного отверстия равно нулю или напряжению сжатия , при посадке диска на вал с натягом.

Величина напряжения изменяется в зависимости от режима работы двигателя и может быть рассчитана с учетом совместных деформаций вала и диска.

С учётом граничных условий формулы для расчета распределения напряжений по радиусу равномерно нагретого диска запишутся

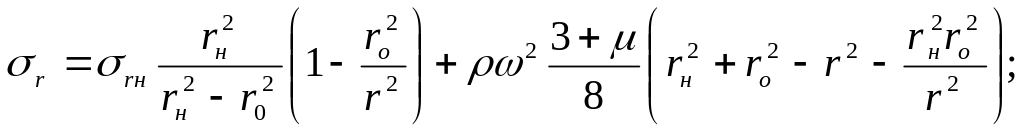
(6.18)

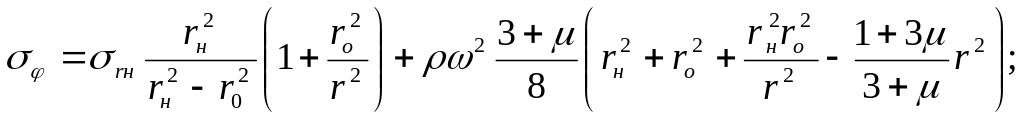
Напряжения и состоят из двух частей- напряжений от внешней нагрузки и напряжений, вызываемых инерционными силами собственной массы диска.

Контурная нагрузка на периферии сплошного диска увеличивает на величину радиальные и тангенциальные напряжения по всему диску.

Напряжения от инерционных сил массы диска увеличиваются с ростом окружной скорости периферии диска и плотности материала .

Изменение относительных напряжений по радиусу вращающегося с угловой скоростью сплошного диска и диска с центральным отверстием рис.5.3 показывают, что тангенциальные напряжения на контуре центрального отверстия в два раза больше напряжений в центре сплошного диска.

В неравномерно нагретом неподвижном диске рис.6.4 относительные напряжения на контуре центрального отверстия также примерно в два раза превышают напряжения в центре сплошного диска.

Изменение напряжений по радиусу диска рис.6.4 построены для параболического закона распределения температуры по радиусу

, (6.19)

где - разность температур в центре и на периферии диска.

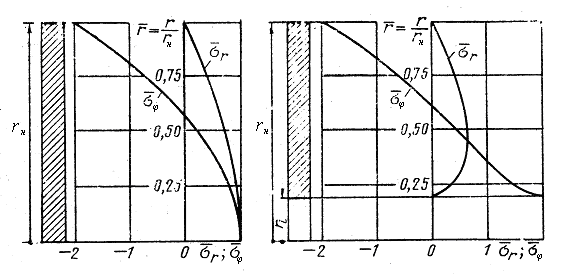Рис.6.4 Распределения напряжений по радиусу неравномерно нагретого невращающегося диска: а - диск сплошной; б- диск с отверстием; ;

При , на периферии диска возникают сжимающие (отрицательные) тангенциальные напряжения, обусловленные стремлением диска на этих радиусах расшириться больше, чем это допускают более холодные внутренние участки диска.

При выключении двигателя обод диска турбины остывает быстрее, чем центр, при этом становится отрицательной, напряжения и меняют свои знаки на противоположные. То есть, при пусках и остановах ГТД, в дисках газовых турбин возникают знакопеременные напряжения, которые могут быть причиной появления трещин из-за малоциклической усталости материала диска.