2.3. Определение частоты колебания лопатки в поле центробежных сил
При вращении ротора на лопатку действует центробежная сила, которая повышает частоту собственных колебаний. Центробежная сила стремится выпрямить ось лопатки, отклоняющуюся при колебаниях.
Центробежная сила приводит к повышению жёсткости лопатки, как натяжение струны в музыкальных инструментах. Влияние центробежной силы возрастает с увеличением закрутки лопатки, угла установки. Бандажная полка также повышает влияние центробежной силы на увеличение собственной частоты колебаний.
Кроме того, в конструкциях, где хвостовик лопатки устанавливается свободно в диске, центробежная сила увеличивает защемление хвостовика лопатки и тем самым повышает частоту собственных колебаний.
Определение частоты колебаний лопатки в поле центробежных сил проведем энергетическим методом. Рассмотрим колебание лопаток с жесткой заделкой в ободе диска в плоскости наименьшей жесткости.
Лопатку
представим как упругую невесомую балку
с приведенной массой на конце (рис.2.8).
К массе приложена центробежная сила
При
свободных колебаниях сумма потенциальной
и
кинетической
энергий
должна оставаться постоянной
(2.56)
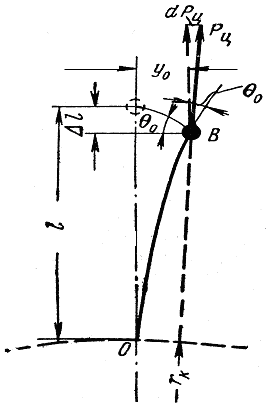
Рис.2.8. К расчету частоты
колебаний лопатки в поле
центробежных сил
В
процессе колебаний приведенная масса
на упругой балке отклонится на угол
,
при этом центробежная сила совершает
работу. Пренебрегаем ввиду малости
окружной составляющей центробежной
силы
,
получим максимальную работу центробежных
сил при максимальном прогибе
(2.57)
где,
ввиду малости
можно принять
,
а
,
-
максимальный прогиб и угол наклона
лопатки.
Примем, что форма упругой линии лопатки близка к форме упругой линии балки, нагруженной сосредоточенной на конце силой Р, то потенциальная энергия деформации стержня будет равна этой работе
(2.58)
Прогиб от силы Р определится
(2.59)
где
- коэффициент жесткости.
Подставим
значения
из равенства (2.59)в зависимость (2.58),
получим
.
(2.60)
Кинетическая энергия соответствующая максимальной скорости, равна
(2.61)
При колебаниях масса перемешается по гармоническому закону
(2.62)
-
круговая частота лопатки, находящейся
в поле центробежных сил.
Дифференцируя уравнения (2.62), получим
(2.63)
Подставим (2.63) в (2.61) получим зависимость
(2.64)
Подставляем полученные выражения для потенциальной и кинетической энергии в (2.56), получим
(2.65)
откуда
(2.66)
Подставим в (2.66) зависимости для прогиба (2.59) и угла наклона от силы Р
и
учитывая, что
получим
(2.67)
Обозначим
,
тогда (2.67) запишется
,
(2.68)
где
круговая частота колебаний неподвижной
лопатки
Линейные частоты связаны с круговыми соотношениями
Частота
собственных колебаний лопатки с учётом
центробежной силы
определяется
частотой собственных колебаний при
неподвижном роторе
и
частоты колебаний идеально гибкой
лопатки находящейся в поле центробежных
сил
(2.69)
Расчёт частот собственных колебаний лопатки с учётом всех факторов сложен, поэтому рассмотрим полуэмпирические зависимости.
Для расчёта первой собственной частоты колебаний лопатки коэффициент В определяется:
- лопатка с постоянным по длине сечением
- лопатка с переменным по длине сечением
- лопатка закрученная, переменного сечения
где
-
средний по длине угол закрутки лопатки,
-
средний радиус лопатки;
-
длина лопатки.