6. Контекстно-свободные грамматики. Основные определения.

Грамматики представляют собой наиболее распространенный класс описаний языков. При описании грамматики необходимо начать с определения алфавита языка, который задается как набор допустимых терминальных символов. Кроме того, необходимо определить набор правил вывода вида a->b с помощью которых строятся все цепочки языка. В левой и правой части этих правил могут встречаться специальные нетерминальные символы; в процессе вывода нетерминальные символы заменяются с помощью соответствующих правил до полной замены на соотвествующие терминалы. Наконец, грамматика должна включать в себя начальный символ , или аксиому, с которой начинается получение любого предложения языка. Итак, грамматика определяется как следующая четверка: , где

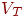• - конечное множество терминальных символов;

• - не пересекающееся с конечное множество нетерминальных символов;

• - конечный набор порождающих правил вида ( , ), где ,

• - начальный символ, где

По классификации Хомского: Грамматика называется:

• выровненной вправо (праволинейной) , если любое правило из имеет вид или , где , - нетерминалы, а - терминал (возможно, пустой).

• контекстно-свободной (бесконтекстной) , если любое правило из имеет вид , где - нетерминал, - нетерминал или терминал

• контекстно-зависимой (неукорачивающей) , если все правила из имеют вид , где

• общего вида (без ограничений) , если грамматика не удовлетворяет ни одному из указанных выше ограничений.

7. Задание кс грамматики. Способы задания грамматик: синтаксические диаграммы, форма Бекуса-Наура.

Знак – графическое начертание.

Символ – знак, в который вложен смысл.

Словарь – набор слов, из которых строятся конструкции языка.

Терминальные символы (терминалы) – слова из словаря, из которых строятся цепочки (a,b,c).

Нетерминальные символы – вспомогательные символы, требующиеся для построения правил грамматики (<A>,<B>,<C>).

Правило грамматики – выражение, в левой части которого всегда стоит нетерминальный символ, а в правой – цепочка из терминальных и нетерминальных символов, которые показывают, как стоятся синтаксически верные конструкции языка.

<IF> if <логическое_выражение> then <блок>

<A> a<B>b<C>

Формы записи правил:

1. Синтаксические диаграммы

терминал

нетерминал

2. Нормальная форма Бэкуса-Наура (БНФ)

if, else // терминал

<оператор>, <блок> // нетерминал

::= // по определению есть

| // или

[] // необязательная часть

() // повторение

3. Теоретическая форма

<A> a<B><C>

КСГ задается следующими множествами:

1. множество терминалов Lт

2. множество нетерминалов Lн (причем Lт в пересечении с Lн дает пустое множество)

3. множество правил (грамматик)

<A> , где - цепочка из терминальных и нетерминальных символов ( может быть пустой цепочкой)

4. один нетерминал, помеченный как стартовый