5. О пределение периодов колебаний систем с одной степенью свободы:пружинный маятник.

mg=kx0

k*∆x=F

m*x=-kx

x+w0x=0

x=Acos(w0t+φ0)?

5. Определение периодов колебаний систем с одной степенью свободы: математический маятник.

Математическим маятником называется тело массой m, размерами которого можно пренебречь, подвешенная на нерастяжимой и невесомой нити длинной l (рис. 182).

Когда нить висит вертикально, сила тяжести уравновешивается натяжением нити. Если нить отвести на некоторый угол , тог сила Р уже не будет уравновешиваться натяжением нити. Разложим силу тяжести Р на две составляющее Р₁ и Р₂. сила Р₂ будет уравновешиваться натяжением нити, сила Р₁ будет возвращать маятник в положение равновесия; она равна

Если угол мал, то , следовательно,

Знак минус указывает, что сила Р₁ направлена в сторону, противоположную смещению.

Отсюда видно, что при небольших значениях угла сила Р₁ пропорциональна смещению и, следовательно, при небольших амплитудах маятник будет совершать гармоническое колебание. Силы, которые по своем природе не являются упругими, но зависят от величины смещения относительно положении равновесия по такому же закону, как и упругие с илы, называются квазиупругими силами.

Сила Р₁ является примером квазиупругой силы.

Найдем период колебаний математического маятника. Из сравнения формул (203б) и (208) имеем

и окончательно

Из формулу (209) видно, что при небольших амплитудах период колебаний не зависит ни от самой амплитуды, ни от массы маятника.

5. Определение периодов колебаний систем с одной степенью свободы: физический маятник.

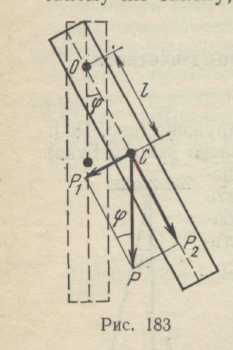
Любое твердое тело, могущее свободно вращаться вокруг неподвижной горизонтальной оси, не проходящий через его цент тяжести, называется физическим маятником (рис.183;0 – ось вращение, расположенная перпендикулярно чертежу, С – центр тяжести тела, l – расстояние от центра тяжести до оси вращения).

Если физический маятник вывести из положения равновесия, отклонив его на некоторый угол , то сила тяжести Р маятника можно разложить на две силы: Р₁ и Р_2. Пологая при небольших углах отклонения и учитывая направление силы Р₁ , обратное отклонению маятника, можно записать

Момент силы Р₁ относительно оси вращения равен . Согласно второму закона Ньютона, для вращательного движения (см. §.28).

где - угловое ускорение; М – момент силы; J – момент инерции тела, или

( 210 )

т.е. угловое ускорение пропорционально угловому пути. Отсюда следует, что при небольших углах отклонение физический маятник будет совершать гармонические колебания.

Найдем период его колебаний. Для этого сравним формулу (202) и (210).

Из сравнения их следует, что

откуда, заменяя Р через , получаем

11.Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение.

Реально во всех колебательных системах действуют силы сопротивления. При малых скоростях F_{сопр х}=-rU_x, r – коэффициент сопротивления.

По второму закону Ньютона: -kx-rU_x=ma_x; -kx-rU^’_x-ma^’’_x=0; mx^’’+rx^’+kx=0; ; ; , где β - коэффициент затухания. X^’’+2β^’+ω²₀x=0 – дифференциальное уравнение затухающих колебаний. Решением данного ДУ является уравнение вида:

x=A₀e^-βtcos(ωt+φ₀). Чем больше коэффициент затухания, тем больше уменьшается амплитуда. ;