1. Взаємодія електричних зарядів. Закон Кулона

Електричний заряд буває позитивним та негативним. Взаємодія частинок однойменного заряду призводить до їх відштовхування, різнойменного – до притягання.

Будь-який заряд є кратним елементарному заряду (заряду електрона), який дорівнює

Кл

Закон Кулона

Кількісно взаємодію заряджених тіл визначає основний закон електростатики, закон Кулона. Він справедливий для точкових зарядів, розмірами яких, за аналогією з поняттям матеріальної точки в класичній механіці, можна знехтувати для даної фізичної задачі.

Математичний вигляд закону для двох точкових зарядів ( ) у системі СІ такий:

,

де - електрична стала.

У системі СГС ця формума має вигляд:

2. Напруженість електричного поля. Принцип суперпозиції

Напруженість електричного поля – це його силова характеристика, що дорівнює силі, з якою поле діє на пробний одиничний заряд.

Принцип суперпозиції полів

Принцип суперпозиції – один із найзагальніших законів у багатьох розділах фізики. Найпростіше формулювання принципу суперпозиції звучить так: результат впливу на частинку кількох зовнішніх сил є просто сума резульаттів впливу кожної із сил.

Найбільш відомий принцип суперпозиції в електростатиці, в якій він стверджує, що електростатичний потенціал, який створюється в даній точці системою зарядів, є сума потенціалів окремих зарядів.

Підкреслимо, що електродинамічний принцип суперпозиції не є непорушним законом природи, а є усього лише наслідком лінійності рівнянь Максвелла, тобто рівнянь класичної електродинаміки. Тому, коли ми виходимо за межі застосовності класичної електродинаміки, цілком варто очікувати порушення принципу суперпозиції.

Якщо E→1(r→) — поле системи зарядів №1, а E→2(r→) — поле системи зарядів №2, то при наявності зарядів обох систем:

E→(r→) = E→1(r→) + E→2(r→).

(4.1)

Рис. 8 пояснює сказане.

Рис.8: Принцип суперпозиції. Під час відсутності заряду q2 на спробний заряд q3 діє сила F→13 = q3E→1, а під час відсутності заряду q1 — сила F→23 = q3E→2. При наявності обох зарядів діюча сила дорівнює їхній сумі, F→3 = F→13 + F→23 = q3E→. Звідси випливає, що в місці перебування спробного заряду E→ = E→1 + E→2.

Найпростіша система складається з одного заряду. Отже, електричне поле системи зарядів дорівнює сумі полів, створюваних кожним зарядом окремо, під час відсутності інших зарядів:

E→(r→) = ∑ j qj ∣r→ −r→j∣2 r→ −r→j ∣r→ −r→j∣ .

(4.2)

Тут qj,r→j — заряд і радіус-вектор j-го заряду. Правило додавання (4.1)називають принципом суперпозиції, а формула (4.2)є наслідком принципу суперпозиції і закону Кулона.

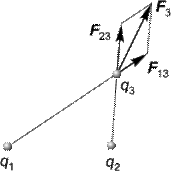
Досліди показують, якщо на електричний заряд q діють одночасно електричні поля декількох зарядів, то результуюча сила дорівнює геометричній сумі сил, що діють з боку кожного поля окремо. Ця властивість електричних полів означає, що ці поля підлягають принципу суперпозиції: якщо в заданій точці простору різні заряджені частинки створюють електричні поля напруженістю , , і т.д., то результуюча напруженість поля в цій точці дорівнює геометричній сумі напруженостей полів частинок, тобто: .

Завдяки принципу суперпозиції для знаходження напруженості поля системи заряджених частинок у будь-якій точці А досить знати вираз для напруженості поля точкового зарядженого тіла і додати вектори за правилом паралелограма (рис. 8):

Рис. 8

Принцип суперпозиції (накладання) полів означає, що електричні поля під час накладання не впливають одне на одне.

Принцип суперпозиції дозволяє обчислити напруженість поля довільної системи зарядів, а не тільки точкових, зокрема і рівномірно зарядженої площини.

За рівномірного розподілу електричного заряду q по поверхні площею S поверхнева густина заряду s є сталою і дорівнює:

.

У фізиці доведено, що напруженість електричного поля нескінченої площини з поверхневою густиною заряду s однакова в довільній точці простору і дорівнює:

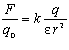, (4.1.8)

де e0 - електрична стала.

Формулу застосовують для розрахунку напруженості електричного поля біля заряджених тіл у тому разі, коли форма рівномірно зарядженої поверхні близька до площини і відстань від точки, в якій визначається напруженість поля, до поверхні тіла значно менша від розмірів тіла і відстані до краю зарядженої поверхні.

З рис. 7 видно, що напруженості полів, створених обома площинами, напрямлені в один бік. Отже, геометрична сума (згідно з принципом суперпозиції полів) є їх арифметичною сумою:

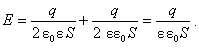
Поза площинами пластин їх напруженості напрямлені протилежно. Тому результуюча напруженість поля поза площинами дорівнює нулю і електричного поля в цих частинах простору немає.

Принцип суперпозиції є експериментальним фактом. В електродинаміку він розглядається як абсолютно точний у тім змісті, що ніякі відхилення від нього не виявлені. Принцип суперпозиції для електричного поля не настільки очевидний, як могло б показатися на перший погляд.

Наприклад, можна припустити, що він порушується в дуже сильному полі аналогічно тому, як у твердому тілі пружні напруження можна складати тільки за умови, що вони досить малі (при великих деформаціях тіло руйнується).

Однак експерименти свідчать, що навіть на поверхні важких ядер, де електричне поле досягає величезних значень, принцип суперпозиції виконується. Інша справа, що при полях, приблизно в 100 разів менших, виявляються ефекти поляризації вакууму в результаті народження електрон-позитронних пар. Це приводить до квантово-механічної нелінійності взаємодії зарядів.

3. Теорема Остроградського-Гаусса. Вектор одиничної індукції

4. Теорема Остроградского-Гаусса

5. Поток вектора a через произвольную замкнутую поверхность S равен интегралу дивергенции этого вектора по объему V, ограниченному этой поверхностью:

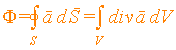
   (2.15)

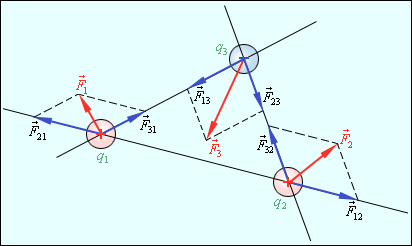
6. Разобъем весь объем, заключенный внутри поверхности S на элементарные кубики типа изображенных на рис. 2.7. Грани всех кубиков можно разделить на внешние, совпадающие с поверхностью S и внутренние, граничащие только со смежными кубиками. Сделаем кубики настолько маленькими, чтобы внешние грани точно воспроизводили форму поверхности. Поток вектора a через поверхность каждого элементарного кубика равен

7. ,

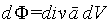8. а суммарный поток через все кубики, заполняющие объем V, есть

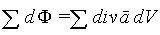
   (2.16)

9. Рассмотрим входящую в последнее выражение сумму потоков dФ через каждый из элементарных кубиков. Очевидно, что в эту сумму поток вектора a через каждую из внутренних граней войдет дважды.

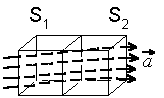
   Рис. 2.8

   Рассмотрим два смежных кубика , поверхности которых обозначены как S1 и S2 (рис. 2.8), причем смежная грань входит как в S1 так и в S2. Очевидно, что при подсчете потока через S1 угол между внешней нормалью к этой грани и вектором а острый и вклад от этой грани в поток будет положительным. А при подсчете потока через S2 вклад от этой грани будет, очевидно, отрицательным.

10. Тогда полный поток через поверхность S=S₁+S₂ будет равен сумме потоков через только внешние грани, поскольку сумма потоков через внутреннюю грань даст ноль. По аналогии можно заключить, что все относящиеся к внутренним граням члены суммы в левой части выражения (2.16), сократятся. Тогда, переходя в силу элементарности размеров кубиков от суммирования к интегрированию, получим выражение (2.15), где интегрирование производится по поверхности, ограничивающей объем.

11. Заменим в соответствии с теоремой Остроградского-Гаусса поверхностный интеграл в (2.12) объемным

12. 

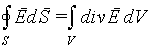
13. и представим суммарный заряд как интеграл от объемной плотности по объему

14. 

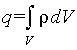
15. Тогда получим следующее выражение

16. 

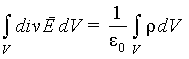
17. Полученное соотношение должно выполняться для любого произвольно выбранного объема V. Это возможно только в том случае, если значения подинтегральных функций в каждой точке объема одинаковы. Тогда можно записать

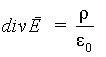
    (2.17)

18. Последнее выражение представляет собой теорему Гаусса в дифференциальной форме.

Ве́ктор електри́чної інду́кції — кількісна характеристика електричного поля у суцільному середовищі.

,

де  — вектор поляризації.

Здебільшого позначається латинською літерою .

4. Потенціал електричного поля

Робота електричного поля при переміщенні заряду. Потенціал. Різниця потенціалів.. Зв`язок між напругою і напруженістю однорідного електричного поля. Робота поля при переміщенні електричного заряду

 

 

5. Енергія і густина енергії електричного поля