3.1.8. Применение теоремы Гаусса для расчетаэлектростатических полей

В случае электростатических полей, обладающих той или иной симметрией (осевая и сферическая симметрия, однородное поле), теорема Гаусса позволяет достаточно просто получить выражение для модуля

вектора . При применении теоремы Гаусса выделяют следующие этапы: 1) из симметрии распределения зарядов определяют направление вектора в каждой точке поля; 2) выбирают произвольную замкнутую поверхность и рассчитывают поток вектора через нее. Поверхность должна содержать внутри себя заряд (часть заряда), создающий поле, и отражать симметрию поля (цилиндр, сфера); 3) рассчитывают заряд, попадающий внутрь поверхности; 4) применяют теорему Гаусса для определения модуля вектора .

Рассмотрим конкретные примеры применения теоремы Гаусса.

Пример 1. Электрическое поле равномерно заряженной по поверхности бесконечно протяженной плоскости. Поле плоского конденсатора.

1 этап. Введем поверхностную плотность заряда . Для этого на заряженной поверхности вблизи какой-либо ее точки выбирают элементарную площадку dS, содержащую заряд dq, и рассчитывают по формуле

(3.30)

т.е. представляет собой заряд, приходящийся на единицу поверхности. Если плоскость заряжена равномерно, то тогда во всех ее точках будет одинаковой ( = const), и поэтому поле такой бесконечно протяженной плоскости является однородным - линии представляют собой прямые, перпендикулярные к ней; во всех точках поля модуль одинаков (рис.3.10,а).

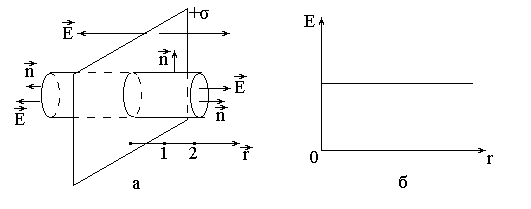
Рис.3.10

2 этап. Выбираем замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к плоскости (рис.3.10,а). Тогда поток Ф_Е через боковую поверхность будет равен нулю ( = 90, линии не пересекают боковой поверхности), и поэтому остается поток только через основания площади

.

3 этап. Рассчитаем заряд плоскости, попадающий внутрь цилиндра

4 этап. Применяем теорему Гаусса (формула(3.29)) для расчета модуля вектора :

;

(3.31)

где учтен случай отрицательно заряженной плоскости.

На рис.3.10,б приведен график зависимости модулю вектора поля плоскости в зависимости от расстояния r от нее.

Формула (3.31) позволяет найти разность потенциалов между двумя точками поля, находящимися на расстояниях и от плоскости (рис.3.10,а).

(3.32)

где знак «+» берется для положительно заряженной плоскости.

Формула (3.31) также позволяет провести расчет поля плоского конденсатора как поля двух параллельных плоскостей с равными по модулю и противоположными по знаку поверхностными плоскостями зарядов (рис.3.11,а).

Используя принцип суперпозиции электростатических полей, можно сделать вывод о том, что поле конденсатора существует между его пластинами (рис.3.11,б), а модуль вектора этого поля равен:

(3.33)

где - модуль заряда одной из пластин конденсатора площадью S.

Оценим разность потенциалов φ1- φ2 (или напряжение U) между обкладками конденсатора, находящимися на расстоянии d друг от друга. Для этого используем формулы (3.21) и (3.33).

(3.34)

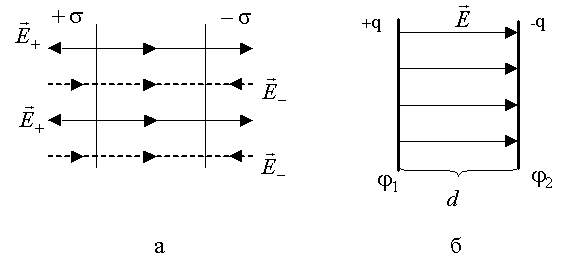
Рис.3.11

Пример 2. Поле равномерно заряженной бесконечно длинной прямолинейной нити.

1 этап. Введем линейную плотность заряда нити. Для этого на заряженной нити выбираем элемент длины dl, содержащий заряд dq , и рассчитываем по формуле

(3.35)

т.е. представляет собой заряд, приходящийся на единицу длины нити.

Для равномерно заряженной нити во всех ее точках будет одинаковой

( = const), поэтому поле такой нити обладает осевой симметрией - линии представляют собой прямые, выходящие из нити и лежащие в плоскостях, перпендикулярных к ней (рис.3.12,а). Причем на одинаковых расстояниях от нити, т.е. на цилиндрических поверхностях, модуль будет одинаковым.

2 этап. Выбираем замкнутую поверхность в виде цилиндра, имеющего высоту H и радиус r; ось цилиндра совпадает с нитью. Поток через основания цилиндра равен нулю (α=900) и поэтому остается поток только через его боковую поверхность

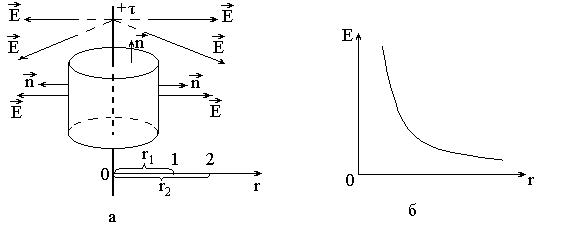
Рис.3.12

3 этап. Рассчитываем заряд отрезка нити длиной Н, попадающий внутрь цилиндра,

.

4 этап. Применяем теорему Гаусса для расчета модуля вектора :

;

(3.36)

Формула (3.36) позволяет оценить разность потенциалов между двумя точками, находящимися на расстоянии и от нити (рис.3.12,а).

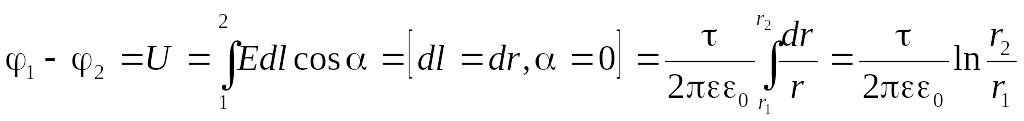(3.37)

На рис.3.12,б приведен график зависимости модуля вектора поля нити от расстояния r до нее.

Пример 3. Поле равномерно заряженной по поверхности сферы (заряженной металлической сферы или шара) радиуса R и заряда q

1 этап. Поле такой сферы обладает сферической симметрией - линии представляют собой прямые, выходящие из центра положительно заряженной сферы заряда q (рис.3.13,а). Причем на одинаковом расстоянии от центра сферы, т.е. на сферических поверхностях, модуль будет одинаковым.

2 этап. Выбираем вспомогательную замкнутую поверхность в виде сферы, имеющей радиус r > R. Рассчитаем поток ФЕ через эту замкнутую поверхность

r > R:

3 этап.

.

4 этап

.

Аналогичный расчет для расстояний r<R приводит к тому, что внутри сферы электрического поля нет, т.к. в этом случае внутрь вспомогательной поверхности, имеющей радиус r, заряд q сферы не попадает ( =0).

r<R:

E=0.

Из записанных выше для формул следует, что внутри сферы поле отсутствует, а за ее пределами оно совпадает с полем точечного заряда q, помещенного в центр сферы. Это позволяет сразу же записать формулы и для потенциала поля сферы:

(3.38а)

(3.38б)

Графики зависимости Е и φ от расстояния r от центра сферы приведены на рис.3.13,в,б.

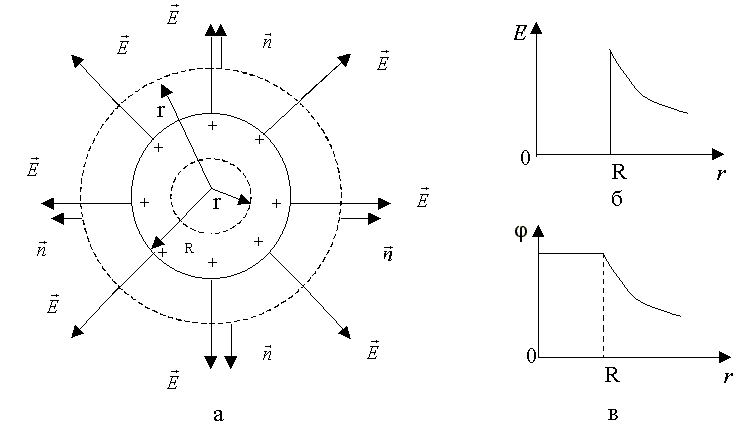
Рис.3.13

Как видно из формул (3.38), на поверхности сферы (r=R) справедливы следующие равенства:

(3.39)

где в формулы введена поверхностная плотность заряда .

В заключение отметим, что графики зависимости потенциала от расстояния r для электростатических полей, создаваемых нитью и плоскостью, не приводятся в связи с тем, что не удается выбрать наиболее удобно нулевой уровень отсчета потенциала, поэтому были записаны только формулы для разности потенциалов между двумя точками поля.

Далее также отметим, что помимо поверхностной и линейной плотностей заряда также вводят и объемную плотность заряда ρ

(3.40)

т.е. ρ представляет собой заряд, приходящийся на единицу объема.