3.1.5. Работа сил электрического поля. Разность потенциалов.Формула связи вектора напряженности и потенциала

Запишем формулы для работы сил электростатического поля по перемещению точного заряда из точки 1 в точку 2. Учитывая выражения (3.5), (3.7), получим:

(3.19а)

(3.19б)

где - вектор элементарного перемещения.

Величину называют разностью потенциалов. Она характеризует работу сил электростатического поля по перемещению заряда из одной точки поля в другую и равна отношению этой работы к величине переносимого заряда

(3.20)

Отметим, что непосредственный физический смысл имеет не сам потенциал, определяемый подобно потенциальной энергии с точностью до произвольной постоянной, а разность потенциалов.

Из выражений (3.19), (3.20) можно получить интегральную формулу связи и в которую входят две точки поля

(3.21)

Дифференциальную формулу связи и , справедливую для малой окрестности какой-либо точки поля, можно вывести из выражений для элементарной работы:

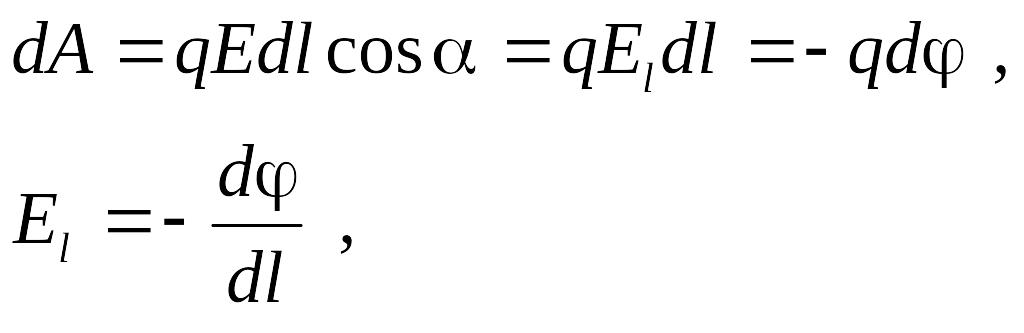(3.22)

где - проекция вектора на направление в пространстве.

В наиболее общем векторном виде выражение, связывающее и , записывается из полученного в механике соотношения между консервативной силой и потенциальной энергией.

;

(3.23)

Итак, в каждой точке поля вектор равен по модулю и противоположен по направлению вектору градиента потенциала, т.е. вектор в каждой точке указывает направление наиболее быстрого убывания потенциала (рис.3.6,а).

С учетом установленных формул взаимосвязи между и следует отметить, что при описании электростатического поля можно было бы ограничиться введением только одной характеристики поля – вектора . Действительно, через вектор можно определить потенциальную энергию заряда, работу по его перемещению, не вводя понятие потенциала. Но понятие потенциала является удобным с точки зрения практического применения электростатических полей.

3.1.6. Графическое изображение электростатических полей

1. Линии вектора . Для графического изображения электростатических полей используют линии вектора - они проводятся так, чтобы в каждой точке линии вектор был направлен по касательной к ней (рис.3.6). Линии нигде не пересекаются, они начинаются на положительных зарядах, заканчиваются на отрицательных или уходят в бесконечность. Примеры графического изображения полей точечных зарядов приведены на рис.3.6,б,в,г. Видно, что

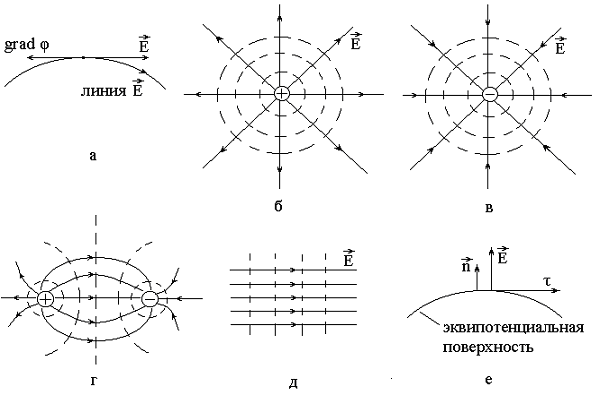
Рис.3.6

для одного точечного заряда линии представляют собой прямые линии, выходящие или входящие в заряд. В случае однородного электрического поля (рис.3.6,д), в каждой точке которого вектор одинаков и по модулю, и по направлению, линии представляют собой прямые линии, параллельные друг другу и отстоящие друг от друга на одинаковом расстоянии.

Графическое изображение полей с помощью линий позволяет наглядно видеть направление кулоновской силы, действующей на точечный заряд, помещенный в данную точку поля, что является удобным для качественного анализа поведения заряда.

Обычно линии проводят так, чтобы их густота (количество линий, пронизывающих перпендикулярную к ним плоскую поверхность фиксированной площади) в каждой точке поля определяла числовое значение вектора . Поэтому по степени близости линий друг другу можно судить об изменении модуля и соответственно об изменении модуля кулоновской силы, действующей на заряженную частицу в электрическом поле.

2. Эквипотенциальные поверхности. Эквипотенциальная поверхность – это поверхность равного потенциала, в каждой точке поверхности потенциал φ остается постоянным. Поэтому элементарная работа по перемещению заряда q по такой поверхности будет равна нулю: . Из этого следует, что вектор в каждой точке поверхности будет перпендикулярен к ней, т.е. будет направлен по вектору нормали (рис.3.6,г). Действительно, если бы это было не так, то тогда существовала бы составляющая вектора ( ), направленная по касательной к поверхности, и, следовательно, потенциал в разных точках поверхности был бы разным ( const), что противоречит определению эквипотенциальной поверхности.

На рис.3.6 приведено графическое изображение электрических полей с помощью эквипотенциальных поверхностей (пунктирные линии) для точечного заряда (рис.3.6,б,в, это сферы, в центре которых находится точечный заряд), для поля, созданного одновременно отрицательным и положительным зарядами (рис.3.6,г), для однородного электрического поля (рис.3.6,д, это плоскости, перпендикулярные к линиям ).

Условились проводить эквипотенциальные поверхности так, чтобы разность потенциалов между соседними поверхностями была одинаковой. Это позволяет наглядно видеть изменение потенциальной энергии заряда при его движении в электрическом поле.

Тот факт, что вектор перпендикулярен к эквипотенциальной поверхности в каждой ее точке, позволяет достаточно просто переходить от графического изображения электрического поля с помощью линий к эквипотенциальным поверхностям и наоборот. Так, проведя на рис.3.6,б,в,г,д пунктирные линии, перпендикулярные к линиям , можно получить графическое изображение поля с помощью эквипотенциальных поверхностей в плоскости рисунка.