3.2.5. Закон Ома и Джоуля-Ленца в дифференциальной форме
В случае неоднородного электрического поля внутри проводника и зависимости удельного сопротивления ρ проводника от выбранной внутри него точки необходимо использовать дифференциальную форму законов Ома и Джоуля - Ленца, справедливую для малой окрестности точки внутри проводника.
Чтобы их получить рассмотрим однородный изотропный проводник длиной l постоянного поперечного сечения площадью S и создадим в проводнике однородное электрическое поле =const. Такие упрощения не скажутся на общности полученных формул.
Из формул законов Ома (3.76) и Джоуля - Ленца (3.81) получим:
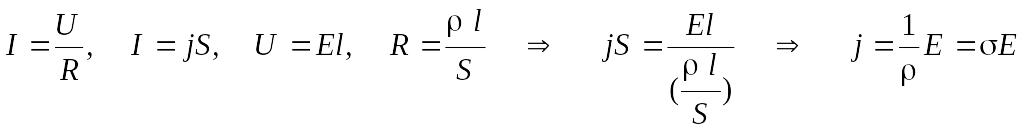
(3.97)
Введем удельную тепловую мощность w
(3.98)
которая определяет количество теплоты dQ, выделяемое в элементарном (бесконечно малом) объеме dV, расположенном в близи точки, взятой внутри проводника, за малое время dt.
Для рассматриваемого здесь вывода элементарные значения dQ, dV, dt можно заменить на их конечные значения Q, V, t , поэтому
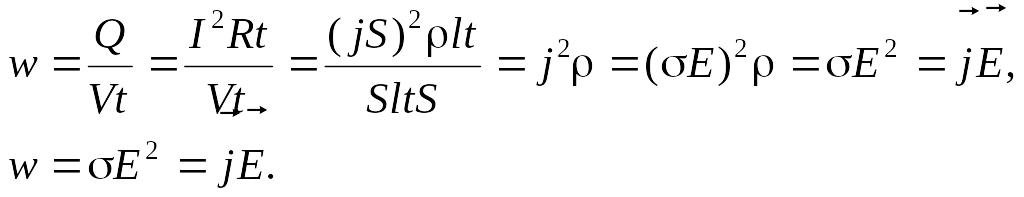(3.99)
Формулы (3.97), (3.99) представляют собой дифференциальную форму законов Ома и Джоуля - Ленца. Введенная в выражение величина называется удельной проводимостью, она связана с удельным сопротивлением ρ формулой
(3.100)
В случае неоднородного участка цепи, когда в проводнике одновременно действуют и сторонние, и кулоновские силы формулы (3.28) и (3.30) примут вид:
(3.101)
(3.102)